Đề thi học kì 2 môn Toán 9 năm 2017-2018 có đáp án - Phòng GD&ĐT Đồng Đăng

 PHÒNG GD&ĐT ĐỒNG ĐĂNG            
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ II NĂM HỌC 2017 – 2018

Môn: Toán 9 (Thời gian làm bài 90 phút)
Câu 1: (2,0 điểm)  Giải các hệ phương trình sau:
         a)   ;                           b)  
Câu 2: (2,5 điểm)  
Cho phương trình bậc hai sau (với m là tham số):
                x2 + (m + 2) x ­  m ­ 3 = 0   (1)
a) Giải phương trình (1) khi m = 3 .
b) Chứng minh rằng phương trình(1) có nghiệm với mọi giá trị của m.
c) Tìm m để phương trình (1) có hai nghiệm và một trong hai nghiệm đó 
gấp đôi nghiệm kia.
Câu 3: (1,5 điểm)  
Một mảnh đất hình chữ nhật có chu vi là 110 m. Nếu tăng chiều rộng thêm 2 
m và giảm chiều dài đi 5 m thì diện tích mảnh đất giảm đi 40 m2. Tính diện tích 
mảnh đất đó.
Câu 4: (4.0 điểm)
Cho đường tròn (O; R) có đường kính AB. Bán kính  OC  vuông góc với 
AB, M là một điểm bất kỳ trên cung nhỏ AC (M khác A, C); BM cắt AC tại H.  
Gọi K là hình chiếu của H trên AB.
a) Chứng minh CBKH là tứ giác nội tiếp.
b) Chứng minh  CA là phân giác của 
c) Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d sao 
cho hai điểm P, C nằm trong cùng một nửa mặt phẳng bờ AB và . Chứng minh  
đường thẳng BP đi qua trung điểm của đoạn thẳng HK.
­­­­­­­­­­­­­­­­­­­­­­­­­­­­­Hết­­­­­­­­­­­­­­­­­­­­­­­­­­­

Cán bộ coi thi không giải thích gì thêm

ĐÁP ÁN, BIỂU ĐIỂM CHẤM KSCLHK2 NĂM HỌC 2017­2018

MÔN:  TOÁN 9
Câu

Nội dung

Điểm

Câu 1: (2,0 điểm)  Giải các hệ phương trình sau:
         a)   ;                           b)  
a)           
Vậy nghi
Câu 1ệm của hệ phương trình là: (x; y) = (2; ­ 1) 
(2.0đ)
b)   
       Vậy nghiệm của hệ phương trình là: (x; y) = (1; 2)

0,75
0,25
0,75
0,25

Câu 2: (2,5 điểm)  
Cho phương trình bậc hai sau (với m là tham số):
                x2 + (m + 2) x ­  m ­ 3 = 0   (1)
a) Giải phương trình (1) khi m = 3 .
b) Chứng minh rằng phương trình(1) có nghiệm với mọi giá trị của m.
c) Tìm m để phương trình (1) có hai nghiệm và một trong hai nghiệm  
đó gấp đôi nghiệm kia.

a)   Thay m = 3 vào phương trình (1) ta được:  x2 + 5x  ­ 6  = 0
0,5 
      Tìm được  x1 = 1;  x2 = ­6
0,25 
      Vậy, nghiệm của phương trình là: x1 = 1;  x2 = ­6
0,25  
b)   Ta có:
Câu 2
0,25
(2,5đ)
       (với mọi m) 
0,25
=> PT (1) luôn có nghiệm với mọi m
0,25 
c)  x2 + (m + 2) x ­  m ­ 3 = 0   (1)  (a = 1; b = m + 2;  c = ­ m – 3)
Ta có:   a + b + c = 1 + m + 2 – m – 3 = 0  
Nếu 
Nếu 
Vậy với  hoặc m = ­ 5  thì phương trình (1) có hai nghiệm và một trong hai nghiệm đó gấp đôi 
nghiệm kia

  0,25 
0,25

0,25
Câu 3:  (1,5 điểm)     Một mảnh đất hình chữ nhật có chu vi là 110 m. Nếu tăng 
chiều rộng thêm 2 m và giảm chiều dài đi 5 m thì diện tích mảnh đất giảm đi 40  
m2. Tính diện tích mảnh đất đó.
Gọi chiều rộng của mảnh đất hình chữ nhật là x; (x > 0, m)
Gọi chiều dài của mảnh đất hình chữ nhật là y; (y > 5, m)

Diện tích của mảnh đất là: x.y 
0,25
Chu vi của mảnh đất là 110m nên ta có phương trình:
     2(x + y) = 110 hay 2x + 2y = 110 (1)
0,25
3
Khi tăng chiều rộng thêm 2 m và giảm chiều dài đi 5 m thì diện tích mảnh đất là : ( x + 2)(y – 
(1,5đ)
5)
 Theo bài ra ta có phương trình: xy – (x + 2)(y – 5) =40
   0,25
 Hay 5x – 2y = 30 (2)
Từ (1) và (2) ta có hệ phương trình: 
0,25
Giải hệ ta được x = 20, y = 35 (thỏa mãn)
Vậy diện tích mảnh đất là :    20. 35 = 700 (m2)

0,25
0,25
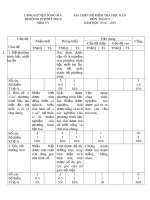
Câu 4. ( 4.0 điểm) Cho đường tròn (O; R) có đường kính AB.  Bán kính  OC 
vuông góc với AB, M là một điểm bất kỳ trên cung nhỏ AC (M khác A, C); BM  
cắt AC tại H. Gọi K là hình chiếu của H trên AB.
a) Chứng minh CBKH là tứ giác nội tiếp.


b) Chứng minh CA là phân giác của 
c) Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d  
sao cho hai điểm P, C nằm trong cùng một nửa mặt phẳng bờ AB và . Chứng 
minh đường thẳng BP đi qua trung điểm của đoạn thẳng HK

S

M

C
H
0,5

P
N
A

K

O

B

d
a) Ta có:  (K là hình chiếu của H trên AB)
           (góc nội tiếp chắn nửa đường tròn)
           Hay 
          Xét tứ giác CBKH có: 
         => Tứ giác CBKH nội tiếp (Tổng hai góc nhau bằng 1800)
b)Ta có: sđ                  (1)
4
           Theo câu a tứ giác CBKH nội tiếp
(4đ)
            sđ
            Hay                            (2)

Từ (1) và (2) => CA là phân giác của 

0,5
0,5
0,25
0,25
   0,25

0,5
0,25

c) Gọi S là giao điểm của  BM với đường thẳng d, N là giao điểm của BP với HK.
Xét PAM và OBM:
Từ giã thiết 
Mặt khác sđ
 (c.g.c)   
     (3) 
Lại có: 
 (4)
Từ (3) và (4) => PA = PS
Vì KH //AS ( cùng vuông góc với AB) nên theo định lý ta lét ta có:
 mà PA = PS => NK = NH  hay BP đi qua trung điểm của HK.

0.25
0,25

0.25
0,25

Lưu ý: Mọi cách giải đúng đều cho điểm tối đa