SKKN cực trị của hàm chứa dấu giá trị tuyệt đối trong đề minh họa 2020

MỤC LỤC :
Đề mục
I
1
2
3
4
II
1
2
III

Nội dung

Trang

Đặt vấn đề
Lý do chọn đề tài
Mục đích nghiên cứu
Đối tượng nghiên cứu
Những điểm mới
Nội dung
Thực trạng vấn đề
Các giải pháp giải quyết vấn đề
Kết luận, kiến nghị

1

2
2
2

2
2
4
4
4– 23
24


I. LÝ DO CHỌN ĐỀ TÀI
1. Lý do chọn đề tài:
Năm học 2019 – 2020 là năm thứ tư áp dụng thi THPT quốc gia môn Toán
bằng hình thức trắc nghiệm khách quan . Muốn làm tốt bài tập trắc nghiệm khách
quan thì ngoài khả năng bao quát kiến thức,học sinh phải được rèn luyên,thực hành
nhiều. Mặc dù vậy,trong quá trình giảng dạy toán tại trường THPT tôi thấy các
SGK hiện nay số lượng bài tập khách quan quá ít, chưa đáp ứng nhu cầu rèn luyện
thực hành của các em . Số tiết dạy trên lớp giáo viên cũng có ít thời gian để giao
bài tập trắc nghiệm phần VD-VDC. Nên học sinh vẫn có những khó khăn,lúng
túng, hay gặp phải sai lầm khi giải các dạng toán này. Các em thường khó khăn,
mất tự tin khi làm bài. Để giúp học sinh giải tốt dạng toán này tôi đã đưa ra giải
pháp là dựa vào các bài toán cụ thể trong đề thi THPTQG và đề minh họa của Bộ .
Từ đó phát triển các bài tập tường tự, cung cấp phương pháp giải và cho học sinh
tiếp cận thông qua các tiết luyện tập trong các giờ học tự chọn, phụ đạo,dạy chuyên
đề hay các buổi ôn thi tốt nghiệp THPT Quốc gia lớp 12. Đó là lí do tôi chọn đề tài:
CỰC TRỊ CỦA HÀM CHỨA DẤU GIÁ

TRỊ TUYỆT ĐỐI TRONG ĐỀ MINH HỌA 2020
2- Mục đích nghiên cứu:
- Rèn luyện, bổ xung , định hướng học sinh vào các chủ đề, chủ điểm mà các em
chưa được trang bị đầy đủ, cũng như đang bị thiếu trong các tài liệu học tập.
- Tạo thêm kênh bài tập để học sinh thảo luận trao đổi. Qua đó nâng cao kiến

thức của mình để áp dụng trong các kỳ thi.
- Góp phần nâng cao tính hiệu quả trong việc dạy học gắn liền với thực tế.
3- Đối tượng nghiên cứu:
- Kiến thức :
+ Cực trị của hàm số ( Giải tích 12).
+ Hàm số ( Đại số 10).
- Học sinh trường THPT Lê Hồng Phong .
2


4- Những điểm mới:
Dựa vào cấu trúc đề thi minh họa của Bộ Giáo dục và Đào tạo, phát triển
các dạng toán phần Vận dụng - Vận dụng cao cho học sinh ôn thi tốt nghiệp năm
2020
4.1. Điểm mới của đề tài.
Sau khi có đề minh họa năm 2020 của Bộ Giáo dục & Đào tạo, tôi nhận
thấy rằng các câu hỏi ở phần VD-VDC đòi hỏi học sinh cần có nhiều bài tập, tài
liệu để làm quen và rèn luyện nhằm phù hợp với đối tượng học sinh khá giỏi học
sinh các lớp chuyên chọn.
Nguyên nhân khách quan:
- Do hệ thống kiến thức vừa dài lại vừa khó trong khi trong phân phối thời lượng
lại quá ngắn
- Chưa tìm ra phương pháp phù hợp
Nguyên nhân chủ quan:
- Khả năng tự học của học sinh còn thấp, số lượng câu hỏi trong Sách giáo khoa
phần này còn hạn chế.
- Giáo viên dạy chưa tâm huyết với nội dung này
4.2. Sáng kiến của đề tài.
Sáng kiến kinh nghiệm này sẽ giúp học sinh tự tin hơn trong việc giải các
câu hỏi mức độ 9 điểm, 10 điểm trong đề thi Tốt nghiệp. Từ đó học sinh không

còn áp lực với các bài toán ở mức độ VD-VDC, các em làm bài có hiệu quả hơn
4.3. Giải pháp của đề tài.
- Người giáo viên lên lớp phải có sự chuẩn bị chu đáo, công phu trong các
tình huống đã được lường trước. Muốn làm được điều đó đòi hỏi chúng ta phải
bắt tay giải các bài toán đó trước tránh cho chúng ta tính ỷ lại hay sao chép máy
móc.
- Học sinh được tiếp cận với vấn đề một cách tự nhiên, đặt ra các vấn đề cần
giải quyết qua từng ví dụ và định hướng suy luận của giáo viên. Từ đó rèn luyện
kỹ năng quan sát phân tích, tìm tòi và nghiên cứu của các em.
3


II. NỘI DUNG
1. Thực trạng
1.1 Về phía giáo viên
Sử dụng tương đối tốt các kĩ năng về tình toán và phân dạng các câu hỏi
trong mức độ nghiên cứu. Tuy nhiên bài toán phần này nhiều nội dung nên việc
giải các bài toán đó còn gặp nhiều khó khăn và bao quát được các dạng câu hỏi.
Tài liệu thư viện chưa đủ nhiều nên tài liệu tham khảo còn hạn chế
1.2. Về phía học sinh
Đa số học sinh chưa chủ động trong quá trình học tập và tự luyện, các em
còn chưa nhận dạng đầy đủ các dạng toán, ngại khó.
Điều kiện học tập còn khó khăn các em rất ít bài tập tiếp cận với các kiến
thức liên quan.
2. NỘI DUNG ĐỀ TÀI
DẠNG 1: CỰC TRỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI KHI
CHO HÀM SỐ y f x
Câu 1. Cho ham sô
tri cua ham sô

y f

x

y f

co đao ham

f'x

x x 2 4 x2

8.

Sô điêm cưc

x la:

A. 0.

B. 1.

C. 2.

D. 3.

Lời giải
4

f'x 0 xx 2

x

x 0
2

Ta co:
Do f ' x

8 0

x 2

.

chỉ đôi dâu khi đi qua điêm x 0 nên ham sô

f x

co 1 điêm cưc tri

x 0.

Ma f x f x

nêu x 0 va

f x

la ham sô chẵn nên ham sô

f

x

co 1 điêm

cưc tri x 0 .
Câu 2. Cho hàm số
số f

x2

2

y f x

xác định và liên tục trên , có

có bao nhiêu điểm cực tiểu ?
4

f ' x x2

1.

Hàm


A.2.

B.5.

C.7.

D.3

Lời giải

Xét hàm số g x
Ta có g

f x2 2 .

xx 2 2 . f x 2 2

2 x. f x2

2.

x 0
g x 0 2 x. f x 2

2 0

x 0
2

f x

x 0

x2 2 1

2 0

x 1

2

x 2 1

x

3.

Bảng biến thiên:

f x2 2

Nhìn vào bảng biến thiên thì g ( x) có hai cực tiểu x 0 . Do đó hàm
có 3 cực tiểu.
Câu 3. Cho

hàm số

x 1 x 12 x 2 1

f'x

y f x

xác

định và liên
f x x

Hàm số

tục trên , có

sẽ

đạo hàm

có tối đa bao nhiêu điểm cực

trị?
A. 3.

B. 5.

C. 7.

D. 9.

Lời giải

Xét hàm số g

x

f x x
x 1
g x 0

2

Ta có

g

x

f'x 1 x 1 x 1 x 2.

x 1

x 2

.

Ta thấy x 1 và x 2 là các nghiệm đơn còn x 1 là nghiệm kép hàm số
cực trị phương trình
cực trị.

gx0

có tối đa 3 nghiệm. Nên hàm số
5

fxx

gx

có 2 điểm

có tối đa 5 điểm


4

f

y f x

5

3

x
x 1 x m x 3
Câu 4. Cho hàm số
với mọi
có đạo hàm
trị nguyên của tham số m5;5
để hàm số
x
. Có bao nhiêu giá
f x có 3 điểm cực trị?

gx

A.3.

B. 4.

C.5.

D. 6.

Lời giải
x 1 0
f x 0

x

x m 0

x m

x 3 0

(x

1 là

x

nghiệm bội 4 , x

+ Nếu m
y
hàm số

1

1 thì

3
m là

phương trình

f

nghiệm bội 5 , x
x

3 là

nghiệm bội 3 )

0

có 2 nghiệm bội lẻ là x 3; x 1
f x
gx
f x
có hai điểm cực trị âm. Khi đó hàm số

có một
m 1

điểm cực trị là x
+ Nếu m

3 thì

0 nên

không thỏa mãn yêu cầu đề bài.

phương trình

fx

f

x

hàm
không
có cực
số
nên msố
3 không
thỏa mãn
yêutrị
cầuhàm
đề bài.

+ Nếu m 3; m 1 thì
điểm cực trị là

fx0

x m; x 3

0

có hai nghiệm bội chẵẵ̃n x

gxfx

1; x

có một điểm cực trị là

có hai nghiệm bội lẻ x m; x 3 hàm số

fx

3

x0

có hai

.

gxfx

fx
có 3 điểm cực trị thì hàm số phải có hai điểm cực trị trái
m 5;5
m 1; 2;3; 4;5
dấu m 0 mà m ,
nên
. Vậy có 5 giá trị của
m thỏa mãn yêu cầu đề bài.

Để hàm số

DẠNG 2: CỰC TRỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI KHI
CHO BẢNG BIẾN THIÊN, BẢNG XÉT DẤU
Câu 1. Cho hàm số
vẽ.

yfx

xác định và liên tục trên

R

có bảng biến thiên như hình


6

Số điểm cực trị của hàm số
A.2.

f x

y

là:

B.3.

C.4.

D. 5.

Lời giải
Từ bảng biến thiên của hàm số

Suy ra hàm số

y

f x

Câu 2. Cho hàm số
sau:

Hỏi đồ thị hàm số
3
A. .

y

yf x

suy ra bảng biến thiên của hàm số y f x

có 5 điểm cực trị.

y g ( x)

xác định liên tục trên R và có bảng biến thiên như

g ( x) 2 có bao nhiêu điểm cực trị?

7
B. .

5
C. .

8
D. .

Lời giải
Từ bảng biến thiên của hàm số
y g ( x) 2 như

y g ( x)

ta có bảng biến thiên của hàm số

sau:

7


Từ đó suy diễn bảng biến thiên hàm số

Vậy số điểm cực trị của đồ thị hàm số
Câu 3. Cho hàm số
f x
như sau

y

f x

y

g ( x) 2

như sau:

là

7

xác định và liên tục trên

Số điểm cực trị của đồ thị hàm số
A. 5.

g ( x) 2

y

y fx 2

2020

B. 4.

điểm.
, có bảng xét dấu của

là:
C. 0.

Lời giải

y f

Xét hàm số

f x

khi x 0

f x

khi x 0

x

Khi đó ta có bảng xét dấu của hàm số

.

y f
8

x

như sau

D. 3.


Suy ra đồ thị hàm số

y

f x

có 5 điểm cực trị.

yfx2
yfx
Suy ra đồ thị hàm số

có 5 cực trị (Tịnh tiến đồ thị hàm số
sang
phải 2 đơn vị thì số điểm cực trị không thay đổi).
Suy ra đồ thị hàm số

2

y f x 2 2020

có 5 cực trị (Tịnh tiến đồ thị hàm số

yfx

lên trên 2020 đơn vị thì số điểm cực trị không thay đổi).

Câu 4. Cho hàm số
hàm

f'x

. Hàm số

yfx

có đạo hàm trên và BBT bên dưới là BBT của đạo

g x f x 2020

A. 2.
Từ BBT ta thấy f x

có bao nhiêu điểm cực trị?

B. 3.

C. 5.
Lời giải

D. 7.

cắt trục hoành tại 2 điểm có hoành độ dương và 1 điểm

có hoành độ âm.
fx

x

có 2 điểm cực trị dương

f

có 5 điểm cực trị

f x 2020

có 5 điểm cực trị (vì tịnh tiến lên trên hay xuống dưới không ảnh
hưởng đến số điểm cực trị của hàm số).
DẠNG 3: CỰC TRỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI KHI
CHO ĐỒ THỊ
9

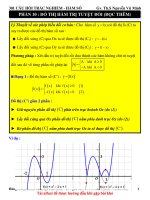
Câu 1. Cho hàm số bậc ba

Hàm số

f x 1 1

y

y

f x

có đồ thị như hình vẽ.

có bao nhiêu cực trị?

6
A. .

7
B. .

D. 5.

8
C. .
Lời giải

y f

x 1 1

Xét hàm số
y

Ta có

y 0

x 1
x 1

x 1

1

f
x 1 ( Điều kiện

x 1 1 0

x 1

)

x 0
x 2

x 1 1 1

x 3

y

không xác định tại

x 1

.

Bảng biến thiên

Dựa vào BBT của hàm số
Câu 2. Cho hàm số
cực trị?

yf x

y

f x 1 1

suy ra hàm số có 5 điểm cực trị.

có đồ thị như sau. Hỏi hàm số

10

yfx

có bao nhiêu điểm


5
A. .

7
C. .

6

B. .

D. 8.

Lời giải
Do hàm số

x

y f

suy ra đồ thị

C
1

là hàm số chẵẵ̃n nên từ đồ thị

của hàm số

trái trục tung của đồ thị

Từ đồ thị

C

1

C

của hàm số

C

của hàm số

y f x

ta

yf x bằng cách xóa bỏ phần đồ thị phía bên

, phần đồ thị còn lại thì lấy đối xứng qua trục tung.
y f x

ta suy ra đồ thị

C

2

của hàm số

y f x

C
bằng cách giữ nguyên phần đồ thị phía bên trên trục hoành của đồ thị 1 , phần
đồ thị còn lại thì lấy đối xứng qua trục hoành và xóa phần đồ thị phía dưới trục
hoành.

Ta có đồ thị hàm số

y

Dựa vào đồ thị hàm số

f x

y

Câu 3.Cho hàm số bậc ba:
như hình bên.

f x

f x

ta thấy hàm số có 7 điểm cực trị.
ax 3 bx 2 cx d , a 0, a , b, c , dcó đồ thị

11


Tập tất cả các giá trị của tham số m để hàm số
là

A.S

1;3.

B.S

1;3.

C.

; 1

yfxm

3;

có đúng ba điểm cực trị

. D.S

; 3

1;

Lời giải

y f x
+) Số điểm cực trị của hàm số
bằng A B với A là số điểm cực trị của
yfx
yfx
hàm số
và B là số giao điểm của đồ thị hàm số
với trục hoành
( không tính các điểm trùng với các điểm đã tính ở A ).
yfx
yfxm
+) Vì hàm số
có hai điểm cực trị nên hàm số
cũng luôn có hai điểm
cực trị.
fxm0
Do đó yêu cầu bài toán xảy ra Phương trình
có đúng một nghiệm đơn
khác cực trị.
f x
m 0
Để phương trình
có đúng một nghiệm đơn, ta cần:
Oy
y f x

+) Tịnh tiến đồ thị hàm số
dọc theo
xuống dưới tối thiểu 1 đơn vị
(1)
Oy
y f x
+) Hoặc tịnh tiến đồ thị
dọc theo
lên trên tối thiểu 3 đơn vị (2)
Từ đồ thị hàm số

m 3

y f x
ta được:

m

1

.

S; 1 3;

Vậy: tập tất cả các giá trị m là:
Câu 4. Cho hàm số y f x

.
có đạo hàm y f x

liên tục trên và có đồ thị

như hình dưới.

Có bao nhiêu số nguyên m 2020; 2020 để hàm số y f x 1 m có nhiều điểm cực
trị nhất?
12


A. 2024 .

B. 2025 .
x

f x 0

D. 2016 .

Lời giải
2

x

Từ đồ thị suy ra
y f

C. 2018.

2

5

x

x 1 myf

.

x 1 m

x 1 f

x 1 m; x 1

x 1

Ta có
y 0

x 1 m 2

1

x 1 m 2

2

x 1 m 5

3.

Chú ý rằng, hàm số đạt cực trị tại x 1vì tại đó

fx

không xác định và đổi dấu.

1 2 3
Hơn nữa nếu các phương trình ; ; đều có 2 nghiệm phân biệt thì các
nghiệm đó luôn đôi một khác nhau và khác 1.
y 0
Hàm số có nhiều điểm cực tri nhất khi và chỉỉ̉ khi
có nhiều nghiệm nhất
m 2 0

2

m 2 0 m
1

;

2

;

3

.

m 5 0

đều có 2 nghiệm phân biệt

Kết hợp điều kiện m2020; 2020 ,

m. Suy ra m

Có 2018 số nguyên
cực trị.

để hàm số

m

2020; 2020

3; 4; ....; 2018; 2019;2020

y f

x 1 m

.

có đúng 7 điểm

DẠNG 4: CỰC TRỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI CỦA
HÀM ĐA THỨC CHỨA THAM SỐ
Câu 1. Có

y

x 3 3mx

bao nhiêu giá trị nguyên của tham số
3 m 2 4 x 1 có 3 điểm cực trị?

2

A. 3.

B. 4.

m

để hàm số

C. 5.

D. 6.
x m 2

Lời giải

y
Xét hàm x
Để hàm số

yx

3

3mx 2

Khi đó m

3

y

3mx

2

x 3 3mx

3m2

3m
2

2

4x 1

3m

4 x 1 có

có:

2

y 3x2

6 mx 3 m2 4

4 x 1 có 3 điểm cực trị thì

đúng một cực trị dương.

2 0 m 22 m 2 m1;0;1;2 .
13

0
x m 2.


Câu 2. Có bao nhiêu số nguyên m để hàm số
cực trị.
A. 289 .
288
B.
.

3 x 5 15 x 3 60x m có 5 điểm

y

C. 287 .

D. 286 .

Lời giải

Xét y

3 x 5 15 x 3 60x

Vậy hàm số y

có y

0 15 x 4

45 x 2 60 0 x 2 4 x 2 .

3 x 5 15 x 3 60x có đúng 2 điểm cực

trị x

2; x 2 .

Bảng biến thiên:

Vậy để hàm số có 5 điểm cực trị
3 x 5 15 x 3 60 x m 0
x 5 15 x 3 60x m
144 m 144 .

có tổng số nghiệm đơn và bội lẻ bằng 3.

3

có tổng số nghiệm đơn và bội lẻ bằng 3.

Mặt khác m nên m { 143;...;143}. Có 287 số nguyên thỏa mãn.

Câu 3. Tìm tập hợp tất cả các giá trị thực
y x 3 2 m 1 x 23m x
5
có 5 điểm cực trị.
;

1

A.

4

của tham số m để hàm số

1;.

B.
14

1 ; 1 1;.
2 4

0;1 1;.

D.

C.1;.

4

Lời giải
3x2

Ta có : y

22m 1x

3m

Yêu cầu bài toán tương đương hàm số
dương.
y 0

y x 3 2 m 1 x 2 3mx 5

có 2 điểm cực trị

có 2 nghiệm dương phân biệt.

3x2 2 2 m 1 x 3m 0 có
2

2m 1
2 2m 1
S

P

9 m 0.
m 1
0

3
0

3
m

2 nghiệm dương phân biệt.
1

0 m

1 m 0;

4

4

1;

3

.

Câu 3. Có bao nhiêu số nguyên

m

20; 20

ba điểm cực trị.
A. 17.

B. 18.

Xét x 2 2 x m 0 . Ta có:
- TH1:0m 1

1 m

để hàm số

y

x

2x m
2

2 x 1 có

D. 20.
Lời giải

C. 19.

x22xm0xx22xmx2
2x m
x2 2x m 2x 1

y
-

x 2 m 1 có đúng một điểm cực trị x

TH2:0m 1

x2

x

Khi đó:

x2

2x 2 2 0
y

x

2 x m 0 có hai nghiệm

phân biệt 21 2
y
2x 2 x2 2x m 2
x
2x m

0

2

x

2x m

x 0
0

2x 2 2 0
x

2

2x m

2x m

0

x 0
2

x

x

2x m 0
2

x2

2x m 0

m 0

x 2
m 0

+ Với 0 m 1 Không có giá trị nguyên m thỏa mãn
+ Với m 0 Hàm số có 3 điểm cực trị (Thỏa mãn)
15

0 (Loại).


m19,..., 1

Vậy: Có 19 giá trị nguyên của m thõa mãn điều kiện đề bài.
Câu 4. Cho hàm số y f x
Hàm số

y

f x

liên tục trên

và có đạo hàm

f x x2

x 2

có ít nhất bao nhiêu điểm cực trị?

A. 1.

B. 2.

3
C. .

5
D. .

Lời giải
f x

1x3

Ta có

3

1 x 2 2x C

với

C

là hằng số.

2

Bảng biến thiên của

f x

:

fx
Từ đó suy ra luôn có hai điểm cực trị và có ít nhất một nghiệm không
trùng điểm cực trị.
Do đó hàm số

f x

y

có ít nhất 3 điểm cực trị.
f(x) 1 x4 2x3

4

Câu 5. Cho hàm số

để hàm số

nguyên m2019; 2020
A. 4039.

y f

11 x 2 6 x 2019
2
. Có bao nhiêu giá trị
x m 1 2020

có 7 điểm cực trị.

B. 2019. Lời giải C. 2020.

D. 4040.

x 1
x

f(x) 0

3

6x

2

11x 6 0

x 2
x 3

Hàm số

y f x m 1 2020

lớn hơn 1 m .

có 7 điểm cực trị Hàm số
x m 1 1

f x m 1 0

Ta có:

x m 1 2

x 2 m
x 3 m

x m 1 3

x 4 m
16

yfxm 1

có 3 điểm cực trị

.


2 m 1 m
3 m 1 m
Để hàm số

y f x m 1

có 3 điểm cực trị lớn hơn 1 m thì

4 m 1 m

m R.

nên có 4040 số nguyên thỏa điều kiện bài toán.

Do m2019; 2020
3. BÀI TẬP THAM KHẢO
Câu 1. Cho hàm số
x.

Hàm số

y f x

có đạo hàm

f 1 2018x

y

A. 9.

3

f xx

2x

2

B. 2022 .

C. 11.

f
x
xx
Câu 2. Cho hàm số y f
có đạo hàm
x. Có bao nhiêu giá trị nguyên của tham số
x

B. 4.

Cho hàm số

D. 2018 .

1

5

x m
m5;5

y f ( x)

C. 5.

có đạo hàm

f'(x) x2 x 1

Có bao nhiêu giá trị nguyên của tham số
gx f
x có 5 điểm cực trị?
A. 6.

B. 7.

Câu 4. Xét hàm số

f ( x)

f'x

C. 8.

có đạo hàm

y f 1 2020x

x 3

với mọi

để hàm số

yf x

. Hàm số

f'(x) x2

x 2 2 mx 5 với

mọi

để hàm số
D. 9.

x x 3 3x với mọi x R .

có nhiều nhất bao nhiêu điểm cực trị ?

B. 7.

A. 9 .
Câu 5. Cho hàm số

3

D. 6.

m 10

x R.

Hàm số

, với mọi

có 3 điểm cực trị?

A. 3.
Câu 3.

2x

có nhiều nhất bao nhiêu cực trị.

4

gx f

x3

C. 8.

D. 6.

có đạo hàm trên và BBT bên dưới là BBT của đạo hàm

g x f x 2020

có bao nhiêu điểm cực trị?

17


A. 2.
Câu 6. Cho hàm số

B. 3.
y f x

có

C. 5.

f ( 2) 0

và đạo hàm liên tục trên

D. 7.
và có

bảng xét dấu như hình sau

15 f x 4 2 x 2 2 10 x 6 30x2

Hàm số g x
trị?
A. 2.

B. 3.

Câu 7. Cho hàm số

Hàm số

y

y

f x

f x C

Câu 8. Cho hàm số

C. 5.

y f x

D. 7.

xác định, liên tục trên và có bảng biến thiên:

có nhiều nhất bao nhiêu điểm cực trị?
B. 7.

A. 5.

có bao nhiêu điểm cực

C. 6.

liên tục trên và có bảng biến thiên:

18

D. 3.


Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số
y f x 1 m
có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S
bằng
A. 15.

B. 12.

Câu 9. Cho hàm số y f x

C. 18.

. Hàm số y f x

D. 9.

có đồ thị như hình vẽ dưới

đây.

4f x 2x3 7x28x 1

có tối đa bao nhiêu điểm cực trị?
Hàm số
A. 5.
B. 6.
C. 7.
D. 8.
f x như
Câu 10. Cho hàm số y f x
có đạo hàm liên tục trên và đồ thị

y

hình vẽ bên. Đặt g x f

A. 3.
Câu 11. Cho hàm số

gx

x3

. Số điểm cực trị của hàm số y g x

B. 5.
y f x

có đồ thị

C. 4.
như hình bên

15 f x 1 có bao nhiêu điểm cực trị?

19

là

D. 2.
dưới. Đồ thị hàm


A. 4.

B. 5.
f(x) 1x

4

C. 6.
2x

3

11 x

4

Câu 12. Cho hàm số

S

Câu 13. Gọi
y

. Có bao nhiêu giá trị
x m 1
2020
có 7 điểm cực

f

B. 2019.
là

tập

hợp

D. 7.

6 x 2019

2

nguyên m2019; 2020 để hàm số y
trị.
A. 4039.

2

C. 2020.

các

số

x 3 3mx 2 3(1 m 2 )x m 3 m2

nguyên

D. 4040.
m

để

hàm

số

có 5 điểm cực trị. Tổng các phần tử

của S là
A. 2.

B. 3.

Câu 14. Cho hàm số f x

C. 4.

m 1 x3 5x2

m 3x 3

trị nguyên của tham số m để hàm số
A. 3.
Câu 15. Tổng
y

các

giá

x3 3x2 9x 5

A. 2016 .

B. 1.
trị nguyên
m

x

y f

của

D. 7
. Có tất cả bao nhiêu giá
có đúng 3 điểm cực trị?

C. 2.
tham số

m

D. 4.
để hàm

số

có 5 điểm cực trị là

2

B. 1952 .

C. 2016 .

III.KẾT LUẬN
1. Ý nghĩa, phạm vi áp dụng của đề tài.

20

D. 496 .


Việc phân loại các dạng bài toán đã đem lại hiệu quả cao trong việc học tập và
rèn luyện của học sinh.
Học sinh đã nắm được các dạng cơ bản, rèn luyện nhiều các kĩ năng làm bài tập
và ứng dụng.
Áp dụng trong ôn tập các câu vận dụng - vận dụng cao trong quá trình ôn thi tốt
nghiệp năm 20192020.
Qua điều tra tôi nhận thấy rằng: Sau khi áp dụng việc phân dạng học sinh đã
học tập tiến bộ.
2. Kiến nghị, đề xuất
Sau khi thực nghiệm đề tài này tôi xin đưa ra một số kiến nghị sau:
Cần phát huy tốt việc phân loại các dạng bài tập để học sinh học tập dễ dàng và
hứng thú hơn.
Cần cung cấp và cho học sinh làm quen nhiều với dạng toán nâng cao.
Do khả năng và thời gian có hạn, kết quả của sáng kiến chỉỉ̉ dừng lại ở bước đầu,
nhiều vấn đề chưa được đi sâu, không tránh khỏi những thiếu sót, kính mong
được góp ý để hoàn thiện đề tài.
Tôi xin cam đoan đây là SKKN của mình viết, không sao chép nội dung của
người khác.
XÁC NHẬN CỦA THỦ TRƯỞNG Thanh Hóa, ngày 29 tháng 5 năm 2020
ĐƠN VỊ

(Ký và ghi rõ họ tên)

Trần Lưu Giang

21


IV. Tài liệu tam khảo
[1] Giải tích 12.
[2] Đại Số 10
[3] Đề minh họa môn toán 2020 lần 1.
[4] Đề minh họa môn toán 2020 lần 2.

22