Bài soạn Các truong hop đong dang tam giac vuong
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (426.71 KB, 15 trang )
NhiÖt liÖt chµo mõng
c¸c thÇy gi¸o, c« gi¸o cïng
toµn thÓ c¸c em häc sinh
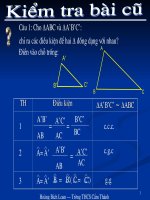
Bài1:Cho tam giác ABC vuông ở A. Đường cao AH. Chứng minh hai tam giác ABC và
HBA đồng dạng
Hai tam giác ABC và ABC Điều kiện cần có Để
B
C
A
A
B C
A
B
C
B
CA
A
B
C
B
C
A
6
10
5
3
CA
'A'C
BC
'C'B
AB
'B'A
==
'C'B'A
)c.c.c(ABC
'C'B'A
)g.g(ABC
'C'B'A
)c.g.c(ABC
B=B (hoặc C=C )
AC
'C'A
AB
'B'A
=
)
2
1
(
AB
'B'A
BC
'C'B
==
Bài2: Hoàn thành vào bảng sau để được khẳng định đúng
Liệu hai tam giác có
đồng dang không?
S
S
S
2
3
1
Kiểm
tra
bài c
ũ
C¸c trêng hîp ®ång d¹ng cña tam gi¸c vu«ng
1) ¸p dông c¸c trêng hîp ®ång d¹ng
cña tam gi¸c vµo tam gi¸c vu«ng
A
B
C
B’
C’A’
'C'B'A
∆
ABC
∆
(A=90
0
; A’=90
0
)
NÕu
B’=B (hoÆc C’=C)
AC
'C'A
AB
'B'A
=
Bµi tËp 1: Hai tam gi¸c sau cã ®ång d¹ng kh«ng?
E
E’
D
F
2,5
5
D’
F’
5
10
H×nh 1
DEF
∆
'F'E'D∆
(c.g.c)
V×:
'D
ˆ
D
ˆ
=
vµ
)
2
1
(
'F'D
DF
'E'D
DE
==
S
S
(= 90
0
)
C¸c trêng hîp ®ång d¹ng cña tam gi¸c vu«ng
(g.g)
C
A
P
R
Q
H×nh 2
B
30
0
60
0
ABC∆
PRQΔ
vµ C=Q=60
0
V×: A = P
1) ¸p dông c¸c trêng hîp ®ång d¹ng
cña tam gi¸c vµo tam gi¸c vu«ng
A
B
C
B’
C’A’
'C'B'A
∆
ABC
∆
(A=90
0
; A’=90
0
)
NÕu
B’=B (hoÆc C’=C)
AC
'C'A
AB
'B'A
=
Bµi tËp 1: Hai tam gi¸c sau cã ®ång d¹ng kh«ng?
S
S
(= 90
0
)
Các trường hợp đồng dạng của tam giác vuông
C
Hình 3
A
1) áp dụng các trường hợp đồng dạng
của tam giác vào tam giác vuông
A
B
C
B
CA
'C'B'A
ABC
(A=90
0
; A=90
0
)
Nếu
B=B (hoặc C=C)
AC
'C'A
AB
'B'A
=
Bài tập 1: Hai tam giác sau có đồng dạng không?
A
B
B
C
3
5
6
10
Theo định lí Pytago trong tam giác vuôngABC
Ta có: AC
2
=BC
2
- AB
2
=5
2
- 3
2
=16
Vậy AC = 4 cm
+ Tương tự tính AC = 8 cm
Ta có: )
2
1
(
8
4
10
5
6
3
===
Nên
CA
'A'C
BC
'C'B
AB
'B'A
==
Suy ra
'C'B'A
)c.c.c(ABC
2) Dấu hiệu đặcbiệt nhận biết hai tam
giác vuông đồng dạng
Định lí1:SGK/82
A
B
C
B
A C
S
S
Các trường hợp đồng dạng của tam giác vuông
1) áp dụng các trường hợp đồng dạng
của tam giác vào tam giác vuông
A
B
C
B
CA
'C'B'A
ABC
(A=90
0
; A=90
0
)
Nếu
B=B (hoặc C=C)
AC
'C'A
AB
'B'A
=
2) Dấu hiệuđặc biệt nhận biết hai tam
giác vuông đồng dạng
Định lí1:SGK/ 82
A
B
C
B
A C
S
GT
KL
AB
B'A'
90 A 'A
C'B'A' ,
0
=
BC
CB
==
ABC
''
ABC ''' CBA
S