- Trang chủ >>
- Đề thi >>
- Đề thi lớp 6
Luyen tap cac truong hop dong dang cua tam giac vuong
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (109.67 KB, 4 trang )
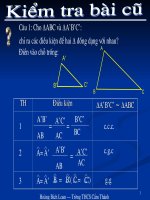
<span class='text_page_counter'>(1)</span>Ngày soạn: 06 /03 /2013 Ngày dạy: 11 /03 /2013. LUYỆN TẬP TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VUÔNG A.MỤC TIÊU - Kiến thức : Hs cũng cố vửng chắc các định lý nhận biết hai tam giác vuông đồng dạng (nhất là trường hộp cạnh huyền và góc nhọn ) Biết phối hợp , kết hợp các kiến thức cần thiết giải quyết vấn đề mà bài toán đặc ra - Kỹ năng : Vận dụng thành thạo các định lý để giải quyết các bài tập từ đơn giản đến khó - Thái độ: Rèn luyện kỹ năng phân tích , chứng minh , khả năng tổng hợp B. CHUẨN BỊ GV : SGK , Bảng phụ, phấn màu, thước thẳng , êke, com pa. HS : SGK , bảng nhóm , máy tính bỏ túi , thứơc thẳng , êke, com pa. C. TIẾN TRÌNH DẠY - HỌC I. ỔN ĐỊNH LỚP (1ph) II. KIỂM TRABÀI CŨ (15 ph) TG HOẠT ĐỘNG GV HOẠT ĐỘNG HS 15 ph a. Nêu các trường hợp đồng dạng của tam giác vuông Cho ABC vuông ở A và A’B’C’ vuông ở A’ có B=40o, Hs lên bảng trình bày bài C=50o. Chứng minh hai tam giải giác đồng dạng? b. Nêu các trường hợp đồng dạng của tam giác vuông Cho ABC vuông ở A và A’B’C’ vuông ở A’ có AC=3cm, BC=4cm, A’C’=6cm, B’C’=8cm. Chứng minh hai tam giác đồng dạng Cả lớp theo dõi nhận xét Gv nhận xét và cho điểm. NỘI DUNG Nêu các trường hợp đồng dạng của tam giác vuông vA’B’C’:B’+C’=90o B’=90o-C=90o-50o=40o Vì B=B’=40o nên ABC A’B’C’ Nêu các trường hợp đồng dạng của tam giác vuông AC BC 1 Vì A' C' B' C' 2 A’B’C’ nên ABC. III. LUYỆN TẬP TG. HOẠT ĐỘNG GV Bài 49 Treo bảng phụ có hình vẽ lên. HOẠT ĐỘNG HS a) Trong hình vẽ có ba. NỘI DUNG Bài 49 SGK tr 84.
<span class='text_page_counter'>(2)</span> bảng 18 ph. GV: Trong hình vẽ có những tam giác nào? Những cặp tam giác nào đồng dạng với nhau? Vì sao?. tam giác vuông đồng dạng với nhau từng đôi một: ABC đồng dạng HBA (B chung) ABC đồng dạng HAC (C chung) HBA đồng dạng HAC ( cùng đồng dạng với ABC ). ABC đồng dạng HBA ( B. chung) ABC đồng dạng HAC (C. chung) HBA đồng dạng HAC ( cùng đồng dạng với ABC ). - Tính BC.. b) Trong tam giác vuông ABC BC 2 AB 2 AC 2 (đ/l Pytago) BC AB 2 AC 2 12, 452 20,52 23,98. - Tính AH, BH, HC. Nên xét cặp tam giác đồng dạng nào?. (cm) - ABC đồng dạng HBA (cmt) . AB AC BC HB HA BA. Hay 12, 45 20,50 23,98 HB HA 12, 45 12, 452 HB 6, 46 23,98. (cm) HA . 20,50.12, 45 10, 64 23,98. (cm) CH = BC – BH = 23,98 – 6,46 17,52 (cm) HS vừa tham gia làm bài dưới sự hướng dẫn của GV, vừa ghi bài.. b) Trong tam giác vuông ABC BC 2 AB 2 AC 2 (đ/l Pytago) BC AB 2 AC 2 12, 452 20,52 23,98. (cm) - ABC đồng dạng HBA (cmt) AB AC BC HB HA BA 12, 45 20,50 23, 98 HA 12, 45 Hay HB . 12, 452 HB 6, 46 23,98 (cm) 20,50.12, 45 HA 10, 64 23,98. (cm) HC = BC – BH = 23,98 – 6,46 17,52 (cm).
<span class='text_page_counter'>(3)</span> Bài 50 (Hình vẽ trong bảng phụ treo lên bảng). Do BC // B’C’ (theo tính chất quang học) ⇒ C=C ' ABC đồng dạng A ' B ' C ' (g.g) AB AC A' B ' A 'C ' AB 36,9 Hay 2,1 1, 62 AB . 2,1.36,9 47,83 1, 62. (cm) HS lớp nhận xét bài làm của bạn.. Bài 51 GV yêu cầu HS hoạt động nhóm để làm bài tập. GV gợi ý: Xét cặp tam giác nào HS hoạt động theo nhóm. có cạnh là HB, HA, HC.. Bài 50 SGK tr 84 Do BC // B’C’ (theo tính chất quang học) ⇒C=C ' ABC đồng dạng A ' B ' C ' (g.g) AB AC A ' B ' A 'C ' AB 36,9 Hay 2,1 1, 62 AB . 2,1.36,9 47,83 1, 62 (cm). Bài 51 tr 84 SGK. GV kiểm tra các nhóm hoạt động. Sau thời gian các nhóm hoạt động khoảng 7 phút, GV yêu cầu đại diện các nhóm lên trình Có thể mời lần lượt đại diện ba nhóm.. IV. VẬN DỤNG – CỦNG CỐ (10 ph) TG 10 PH. HOẠT ĐỘNG GV Nhắc lại các trường hợp đồng dạng của tam giác vuông ?. HOẠT ĐỘNG HS Nhắc lại các trường hợp đồng dạng của tam giác vuông. NỘI DUNG.
<span class='text_page_counter'>(4)</span> V. HƯỚNG DẪN VỀ NHÀ ( 1 ph) - Ôn tập các trường hợp đồng dạng của hai tam giác. - Bài tập về nhà số 52 SGKvà 46, 47, 48, 49 tr 75 SBT. - Xem trước bài 9. Ứng dụng thực tế của tam giác đồng dạng. VI. RÚT KINH NGHIỆM …………………………………………………………………………………………………… …………………………………………………………………………………………………… …………………………………………………………………………………………………… …………………………………………………………………………………………………… …………………………………………………………………………………………………… …………………………………………………………………………………………………… …………………………………………………………………………………………………… (Giáo viên hướng dẫn) (ký duyệt).
<span class='text_page_counter'>(5)</span>