cac truong hop dong dang cua tam giac vuong

xÐt ∆ABC vµ ∆ A'B'C' cã:
'B
ˆ
B
ˆ
=
(gt)
(gt)
0
90'A
ˆ
A
ˆ
==
xÐt ∆ ABC vµ ∆ A'B'C' cã:
(gt)
0
90'A
ˆ
A
ˆ
==
(gt)
=> ∆ ABC ∆ A'B'C' (T/h 2)
Gi¶i:
Gi¶i:
'C'A
AC
'B'A

AB
=
∾
=> ∆ ABC ∆ A'B'C' (T/h 3)
∾
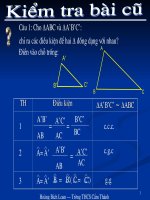
KiÓm tra bµi cò:1/ Cho tam gi¸c vu«ng ABC vu«ng t¹i A vµ
tam gi¸c vu«ng A’B’C’ vu«ng t¹i A’ cã Chøng minh
∆ABC ∆A’B’C’.
'B
ˆ
B
ˆ
=
∾
2/ Cho tam gi¸c vu«ng ABC vu«ng t¹i A vµ tam gi¸c vu«ng
A’B’C’ vu«ng t¹i A’ cã . Chøng minh
∆ABC ∆A’B’C’
'C'A
AC
'B'A
AB
=
∾
B
A
C
B'
A'
C'

xÐt ∆ABC vµ ∆ A'B'C' cã:
'B
ˆ
B
ˆ
=
(gt)
(gt)
0
90'A
ˆ
A
ˆ
==
xÐt ∆ ABC vµ ∆ A'B'C' cã:
(gt)
0
90'A
ˆ
A
ˆ
==
(gt)
=> ∆ ABC ∆ A'B'C' (T/h 2)
Gi¶i:
Gi¶i:
'C'A
AC
'B'A

AB
=
∾
=> ∆ ABC ∆ A'B'C' (T/h 3)
∾
KiÓm tra bµi cò:1/ Cho tam gi¸c vu«ng ABC vu«ng t¹i A vµ
tam gi¸c vu«ng A’B’C’ vu«ng t¹i A’ cã Chøng minh
∆ABC ∆A’B’C’.
'B
ˆ
B
ˆ
=
∾
2/ Cho tam gi¸c vu«ng ABC vu«ng t¹i A vµ tam gi¸c vu«ng
A’B’C’ vu«ng t¹i A’ cã . Chøng minh
∆ABC ∆A’B’C’
'C'A
AC
'B'A
AB
=
∾
B
A
C
B'
A'
C'

1/ áp dụng các trường hợp đồng dạng của
tam giác vào tam giác vuông
a/ Tam giác vuông này có một góc nhọn
bằng góc nhọn của tam giác vuông kia.
b/ Tam giác vuông này có hai cạnh góc
vuông tỉ lệ với hai cạnh góc vuông của tam giác
vuông kia.
TIET48
Đ8. các trường hợp đồng
dạng của Tam giác vuông
Hai tam giác vuông đồng dạng nếu:

? Tìm cặp tam giác đồng dạng trong hình vẽ
B
C
A
H
B

chung
Giải
ã
ã
0
90BAC AHB
= =
+ Xét ABC và HAB có:

Nên HBA HAC( Tính chất tam giác đồng dạng)
(gt)

TIET48 Đ8. các trường hợp đồng dạng của Tam giác vuông
=> ABC HBA ( T/h 3)

C

0
90H

A

==

+ xét ABC và HAC có:
(gt)
chung
=> ABC HAC (T/h 3)
+ Vì ABC HBA



Và ABC HAC