cac truong hop dong dang cua hai tam giac vuong Co Tam

<span class='text_page_counter'>(1)</span>Chuyên đề dạy học tháng 3. Giáo viên dạy : Phan Thị Tâm Trường THCS Nguyễn Bỉnh Khiêm Tổ : Toán –Lý ; Năm học: 2014-2015.

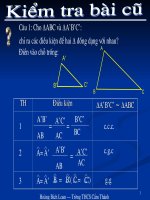
<span class='text_page_counter'>(2)</span> ? Phát biểu các trường hợp đồng dạng của hai tam giác.. Tỡm các cặp tam giác đồng dạng trong hỡnh và giải thớch. D. B 5. 10. E. F. C. A M 2,5. N. K. I 5. P. H.

<span class='text_page_counter'>(3)</span> Có những cách riêng để nhận biết hai tam giác vuông đồng dạng không?.

<span class='text_page_counter'>(4)</span> Hai tam giác vuông đồng dạng với nhau nếu có điều kiện gì? D. B. A. 5. E. N. F. C. M 2,5. 10. K. I. 5. P. H.

<span class='text_page_counter'>(5)</span> Hai tam giác vuông đồng dạng với nhau nếu: a./Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia; Hoặc b./Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia..

<span class='text_page_counter'>(6)</span> ? Các cặp tam giác sau có đồng dạng với nhau không? Vì sao? D'. a). 6. 3. D 2. 1 E. F E'. F'. ∆ DEF ഗ ∆ D’E’F’ (c.g.c). b). Lược giải. C. -Áp dụng định lí Pitago vào hai tam giác vuông tính được AC = 8; A’C’= 4.. C'. 10. A. 6. 5. B. A'. 3. B'. AB sánh AC được BC 2 - Tính và so   ( ) A' B '. A 'C '. B 'C '. 1. - Kết luận: ∆ ABC ഗ ∆ A’B’C’ (c.c.c) (hoặc c.g.c).

<span class='text_page_counter'>(7)</span> . Định lí 1. Nếu cạnh huyền huyền và một vuông một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh cạnh huyền và cạnh góc góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng..

<span class='text_page_counter'>(8)</span> Nêu sự giống và khác nhau giữa trường hợp đồng dạng hai tam giác vuông với trường hợp bằng nhau hai tam giác vuông (ch-cgv) của hai tam giác.. Giống: Đều xét đến điều kiện cạnh huyền và cạnh góc vuông. Khác nhau: Trường hợp đồng dạng: (ch.cgv) Trường hợp bằng nhau:. (ch.cgv) - Cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuôngkia.. - Cạnh huyền và cạnh góc vuông của tam giác vuông này bằng với cạnh huyền và cạnh góc vuông của tam giác vuôngkia..

<span class='text_page_counter'>(9)</span> • Xét ∆ A’B’C’;. Aˆ  900. và ∆ ABC;. B 'C ' 5 1    ; B 'C ' A ' B ' BC 10 2    A' B ' 3 1  BC AB   AB 6 2 . Aˆ 900. có:. C C'. 10. A. 6. 5. B. A'. 3. nên ∆ A’B’C’ ഗ ∆ ABC (Trường hợp đặc biệt) (cạnh huyền – cạnh góc vuông). B'.

<span class='text_page_counter'>(10)</span> Bài toán: Cho hai tam giác đồng dạng ABC và A’B’C’ A' B ' với tỉ k số đồng dạng là AB , hai đường cao tương ứng là AH và A’H’. S A ' B 'C ' 2 Chứng minh A ' H ' rằng:  k k S ABC a/ AH b/.

<span class='text_page_counter'>(11)</span> Định lí 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng Định lí 3: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng..

<span class='text_page_counter'>(12)</span> Bài tập: Khoanh tròn vào câu trả lời đúng. AB 1  và S DEF DE 3. S. Cho ABC DEF co tich tam giac ABC băng ? A. SABC=10cm2. = 90cm2. Diện. B. SABC = 30cm2. C. SABC=270cm. 2. D. SAB =810cm2.

<span class='text_page_counter'>(13)</span> ? Theo em tỉ số nào của hai tam giác đồng dạng đã học liên quan với tỉ số đồng dạng 1./ Tỉ số hai đường trung tuyến tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng 2./ Tỉ số hai đường phân giác tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng 3./ Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng 4./ Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng 5./Tỉ số diện tích của hai tam giác đồng dạngbằng bình phương tỉ số đồng dạng.

<span class='text_page_counter'>(14)</span> Các cách chứng minh hai tam giác vuông đồng dạng: Cách 1. Chứng minh hai tam giác vuông có một cặp góc nhọn bằng nhau. (trường hợp gCách 2. Chứng minh hai tam giác vuông có hai cặp g) cạnh góc vuông tỉ lệ.(trường hợp c-g-c) Cách 3. Chứng minh hai tam giác vuông có cặp cạnh huyền và một cặp cạnh góc vuông tỉ lệ. (trường hợp cạnh huyền - góc nhọn).

<span class='text_page_counter'>(15)</span> E. Bài 1. (Bµi 46/sgk) Trªn hình 50, h·y chØ ra c¸c tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tơng ứng và giải thích tại sao chúng đồng d¹ng.. Giải. D. F. A.  B  90 0 ; A  chung) ∆DAC ഗ ∆BAE ( D. B Hình 50. C.  B  90 0 ; DFE   D  BFC ∆DFE ഗ ∆BFC ( vì đối đỉnh)  B  90 0 ; E  chung) ∆DFE ഗ ∆BAE ( D  90 0 ; C  chung) ∆BCF ഗ ∆DCA ( B D 0    C  vì cùng phụ với Â) EDF  CDA  90 ;E ∆DEF ഗ ∆DCA (.    C  vì cùng phụ với Â) FBC 90 0 ; E ∆BCF ഗ ∆BEA ( ABE.

<span class='text_page_counter'>(16)</span> Bài 2.(Bài 47/SGK) Tam giác ABC có độ dài các cạnh là 3cm; 4cm; 5cm.Tam giác A’B’C’ đồng dạng với tam giác ABC và có diện tích là 2 54 cm .Tính độ dài các cạnh của tam giác A’B’C’.(nên ghi bài toán này dưới dạng GT và KL). Gợi ý:. - Chứng minh ∆ABC vuông và tính diện tích ∆ABC. C' C. S. A ' B 'C ' - Áp dụng định lí 3, k 2 S ABC tính k =đồng ? dạng, - suy Lập ra tỉ số. tính A’B’; A’C’; B’C’.. 5. 4. 54 cm A'. 2. B'. A. 3. B.

<span class='text_page_counter'>(17)</span> HƯỚNG DẪN VỀ NHA - Học, nắm vững các trờng hợp đồng dạng của hai tam gi¸c vu«ng. - BiÕt c¸ch tÝnh tØ sè hai ®ờng cao, tØ sè diÖn tÝch cña hai tam giác đồng dạng. - Làm bài tập 46; 48 ; 49; 50 /84 SGK..

<span class='text_page_counter'>(18)</span>

<span class='text_page_counter'>(19)</span> B. Hướng dẫn bài 48/sgk - Gäi AB lµ chiÒu cao cña cột điện, AC là bóng của cột điện trên mặt đất. -A’B’ lµ chiÒu cao cña thanh s¾t,. B’. A’C’ là bóng của thanh sắt trên mặt đất.. A. C. A’. C’. Suy ra ABC ഗ A’B’C’ và có AC = 4,5m; A’B’ = 2,1m; A’C’ = 0,6m Tính AB = ?.

<span class='text_page_counter'>(20)</span>

<span class='text_page_counter'>(21)</span>