Chuong III 7 Tu giac noi tiep

01:12


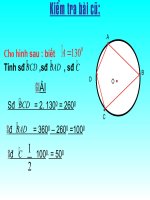
Kiểm tra bài cũ:
Khi nào tam giác được gọi là nội tiếp
đường tròn?

Tam giác được gọi
là nội tiếp đường
tròn khi ba đỉnh của
tam giác nằm trên
đường trịn đó.

B





O

A




C


Ta ln vẽ được một đường
trịn đi qua các đỉnh của một

tam giác.




O





Phải chăng chúng ta cũng làm
được như vậy với một tứ giác?








Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:

?1

b) Vẽ một đường tròn tâm I rồi
a) Vẽ đường trịn tâm O rồi vẽ
vẽ một tứ giác có ba đỉnh nằm
một tứ giác có tất cả các đỉnh

trên đường trịn cịn đỉnh thứ
nằm trên đường trịn đó.
Q
tư thì khơng.
B
A

M

I

M

O

Q

I

C

N

D
N
P

ABCD là tứ giác nội tiếp
đường trịn tâm O

MNPQ khơng là tứ giác nội tiếp
đường tròn tâm I

P


Tiết 48: TỨ GIÁC NỘI TIẾP

1. Khái niệm tứ giác nội tiếp
Định nghĩa:
Một tứ giác có bốn đỉnh nằm trên một đường
tròn được gọi là tứ giác nội tiếp đường tròn
(gọi tắt là tứ giác nội tiếp)


Tiết 48: TỨ GIÁC NỘI TIẾP
Hãy tìm 3 tứ giác nội tiếp và 2 tứ giác không nội tiếp trong hình vẽ
sau
A
B

E

F

O
I

C

D

Các tứ giác nội tiếp là:
ABDE
ABCD
ACDE
Các tứ giác khơng nội tiếp là
AFDE

AIDE


Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:
Định nghĩa:
A, B, C, D (O) <=> ABCD là tứ giác nội tiếp

Tứ giác nội tiếp
có tính chất gì?


Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:
Định nghĩa:
A, B, C, D (O) <=> ABCD là tứ giác nội tiếp
2. Định lí.

90

B

90

80

10 0

110
120

70
180

50

110

10 0

90

80

70

10

60

170

A

130

0

O

140

20

50

20

170

120

10

10 0

70

90

D

60

80

70

60

50

10 0

110

120

160

40
150
140

80
90

170

30

110

180

0

170

10

130

180

10

160

160
20

40

0

150

30

150

140

30

30

130

150

40

160

40

140

60
50

120
20

A 900
A  C
 1800

 900

C

0

C

90

180

130


Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:
Định nghĩa:

10

30

20

140

40

130

60

50

120

70

180

170

160

80
90

10 0

120

110

130

140

150

90

10 0

50

80

110

60

70

70

60

12 0

O

10

20

30

80

10 0

40

90

C

110

70

D

0

110
10 0
90

50
130

140

150

80

100

40

30

160

180

170

A

B
20

10

B 800
 D
 1800

B
 1000
D

80

0

A 900
A  C

 1800

 900
C

0

150

160

170

180

A, B, C, D (O) <=> ABCD là tứ giác nội tiếp
2. Định lí.

60
120

50

130

40
3


M

I
Q

1100
P

N


M

900
I
Q

N

1100
P

 M
 2000 (1800 )
P


Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:
Định nghĩa:
A, B, C, D (O) <=> ABCD là tứ giác nội tiếp

2. Định lí.
P
B
N

A

O
D

N

P

O
C

M

O
Q

M

Q


HOẠT ĐỘNG NHĨM
Bài tốn: Cho tứ giác ABCD nội tiếp trong
đường trịn (O). Chứng minh:

a)

ˆ Dˆ =1800
b) B+

ˆA +Cˆ =1800

Nhóm 1+2+3

Nhóm 4+5+6
A
B
D

O

C


Chứng minh:

0
ˆ
ˆ
A + C = 180

Ta có tứ giác ABCD nội tiếp đường trịn tâm (O)

A = 1 sđBCD


(định lí góc nội tiếp)

2
C = 1 sđDAB

(định lí góc nội tiếp)
2
1 

ˆ
ˆ
 A + C = sđ(BCD + BAD
)
2 Mà sđ BCD
0


A
DAB

360
sđ

0
ˆ
ˆ
=>
A + C = 180
B

D

O

 +D
 = 1800
Chứng minh tương tự : B
C


Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái niệm tứ giác nội tiếp:
Định nghĩa: A, B, C, D (O) <=> ABCD nội tiếp (O)

2. Định lí:
Trong một tứ giác nội tiếp ,tổng
số đo hai góc đối diện bằng 180°
A

B





O


D

Tứ giác ABCD nội tiếp(O) =>

A + C
 =180°
 D
 =180°
B+

C


• Tiết 48: TỨ GIÁC NỘI TIẾP
B

1. Khái nệm tứ giác nội tiếp
* Định nghĩa.

A

(SGK)

O

2. Định lí. Tứ giác ABCD nội tiếp (O)

C

 1800 ; B
 D
 1800

 A  C

D

Bài tập 53. Biết ABCD nội tiếp. Hãy điền vào ô trống trong bảng sau.
Trường hợp
Góc

A

B

C

D

1)

2)

800

3)

4)

5)

600

700

950
400

1050
750

6)

650
740
980


• Tiết 48: TỨ GIÁC NỘI TIẾP
B

1. Khái nệm tứ giác nội tiếp
* Định nghĩa.

A

(SGK)

O

2. Định lí. Tứ giác ABCD nội tiếp (O)

C

 1800 ; B
 D
 1800
 A  C

D

Bài tập 53. Biết ABCD nội tiếp. Hãy điền vào ô trống trong bảng sau.
Trường hợp
Góc

A

B

C

D

1)

2)

800

3)

4)

5)

600

700

950
400

1050
750

6)

650
740
980


• Tiết 48: TỨ GIÁC NỘI TIẾP
1. Khái nệm tứ giác nội tiếp
* Định nghĩa.

B
A

(SGK)

O

2. Định lí. Tứ giác ABCD nội tiếp (O)

C

 1800 ; B
 D
 1800
 A  C

D

Bài tập 53. Biết ABCD nội tiếp. Hãy điền vào ô trống trong bảng sau.
Trường hợp
Góc

1)

2)

A

B

800
700

75
1050



C

D

0

1050

0

100
1100

3)

4)

600





400

650

0

1800  

740

820
850

1400

1150

980

120
750 1800  

5)

106

00    1800 ; 00    1800

6)
0

950


*Học thuộc định nghĩa, định lí thuận
*Xem trước định lí đảo.
*Làm bài tập 54, 55, 56,58 SGK- trang 89,90.

*Tiết sau học tiếp Định lý đảo.