Chuyen de hinh lang tru dung

Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Chủ đề 2: HÌNH LĂNG TRỤ ĐỨNG
A. Tóm tắt lí thuyết
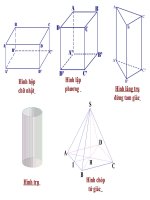
1) Hình lăng trụ đứng
Hình bên là hình lăng trụ đứng. Trong hình này:
- A, B, C, D, A1 ; B1 ; C1 ; D1 là các đỉnh
- Các mặt ABB1 A1 ; BCC1 B1 ;.... là các
hình chữ nhật. Chúng được gọi là
các mặt bên.
- Hai mặt ABCD; A1 B1C1 D1 là hai đáy
Hình lăng trụ đứng trên có hai đáy
là tứ giác nên gọi là lăng trụ đứng
tứ giác, kí hiệu ABCD. A1 B1C1 D1

Hình lăng trụ đứng tứ giác

+ Hình hộp chữ nhật, hình lập phương cũng là những hình lăng trụ
đứng.
Hình lăng trụ đứng có đáy là hình
bình hành được gọi là hình hộp
đứng.
Lăng trụ đứng có hai đáy là tam
giác, tứ giác , ngũ giác thì hình
lăng trụ đứng tương ứng được gọi
là lăng trụ đứng tam giác, lăng trụ
đứng tứ giác, lăng trụ đứng ngũ
giác. (hình 1)
Nguyễn Quốc Tuấn (Tơng biên tâp cua Xuctu.com)

Trang số 203

Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

2) Diện tích xung quanh của hình lăng trụ đứng
 Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích
các mặt bên. Ta có cơng thức

S xq 2 ph

(p là nữa chu vi đáy, h là

chiều cao).
 Diện tích tồn phần của hình lăng trụ đứng bằng tổng diện tích
xung quanh và diện tích hai đáy
Stp S xq  2 Sday

3) Thể tích của hình lăng trụ đứng
 Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều
cao
 Cơng thức V = S.h ( S là diện tích đáy, h là chiều cao)

B. Bài tập mẫu có hướng dẫn giải

Bài tập mẫu 1 : Cho hình lăng trụ đứng tam giác ABC.A’B’C’.
a. Những cặp mặt phẳng nào song song với nhau?
b. Những cặp mặt phẳng nào vng góc với nhau?

Hướng dẫn giai

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 204


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

a. Những cặp mặt phẳng song song là:
mp(ABC)//mp(A’B’C’)
b. Những cặp mặt phẳng vng góc nhau là:
mp(ABC)  mp(AA’B’B)
mp(ABC)  mp(BB’C’C) ;mp(ABC)  mp(AA’C’
C)
mp(A’B’C’)  mp(BB’C’C). mp(A’B’C’) 
mp(AA’C’C)
mp(A’B’C’)  mp(AA’B’B)
Bài tập mẫu 2 : Cho hình lăng trụ đứng tam giác
ABC.DEF. Trong các phát biểu sau phát biểu nào
đúng ?
a) Các cạnh bên AB và AD vng góc với nhau.
b) Các cạnh bên BE và EF vng góc với nhau.
c) Các cạnh bên AC và DF vng góc với nhau.
d) Các cạnh bên AC và DF song song với nhau.
e) Hai mặt phẳng (ABC) và (DEF) song song với nhau.
f) Hai mặt phẳng (ACFD) và (BCFE) song song với nhau.
g) Hai mặt phẳng (ABED) và (DEF) vng góc với nhau.
Hướng dẫn giải
a) Sai vì AB và AD khơng phải là các cạnh bên.
b) Sai vì BE và EF khơng phải là các cạnh bên.
c) Sai vì AC và DF khơng phải là các cạnh bên.

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 205


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

d) Sai vì AC và DF khơng phải là các cạnh bên.
e) Đúng
f) Sai vì Hai mặt phẳng (ACFD) và (BCFE) vng góc nhau
g) Đúng.
Bài tập mẫu 3 : Cho một hình hộp chữ nhật ABCD.A’B’C’D’
Những cặp mặt phẳng nào song song với nhau.
Mặt phẳng (ABCD) vng góc với những mặt phẳng nào.

Hướng dẫn giải
a) Những mặt phẳng song song với nhau là: mp(ABCD)//mp(A’B’C’D’);
mp(AA’D’D)// mp(BB’C’C);

mp(DCC’D’)//mp(AA’B’B)

b) mp(ABCD)  mp(AA’B’B)
mp(ABCD)  mp(BCC’B’)
mp(ABCD)  mp(ADD’D)

Bài tập mẫu 4 : Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có
hai đáy là hai tam giác vuông tại A, A’. Chứng minh
a)
b)

Hướng dẫn giai
Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 206


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

a) AB  AC (ABC vuông tại A)

AB  AA ' (AA’B’B là hình chữ nhật) nên
AB vng góc với hai đường thẳng cắt
nhau AC và AA’ của mặt phẳng (AA’C’C).
Suy ra AB  mp (AA ' C ' C )
b) mp(AA’B’B) chứa AB, mà AB vng góc
với mp(AA’C’C) nên

mp (AA ' C ' C )  mp(AA ' B ' B)
Bài tập mẫu 5 : Một khối gỗ hình lập phương ABCD.A’B’C’D’, có cạnh
bằng a. Người ta cắt khối gỗ theo mặt (ACC’A’) được hai hình lăng trụ
đứng bằng nhau. Tính diện tích xung quanh của mỗi hình lăng trụ đó.
Hướng dẫn giải
2
Ta có AC  a  a a 2cm

Chu vi đáy hình lăng trụ





aaa 2  2 2 a
Diện tích xung quanh của hình lăng
trụ

S xq 2 ph 

2(2  2) a.a
(2  2)a 2 cm 2
2

Bài tập mẫu 6 : Cho hình lăng trụ đứng tam giác ABC.A’B’C’, có
đáy là tam giác ABC cân tại C, D là trung điểm của cạnh AB. Tính
diện tích tồn phần của hình lăng trụ.

Nguyễn Quốc Tuấn (Tơng biên tâp cua Xuctu.com)

Trang số 207


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Hướng dẫn giai
D là trung điểm AB, suy ra CD là chiều cao
tam giác đáy
2
2
Vậy nên DB  5  4  25  16  9 3cm

BB’  AB, áp dụng định lí py-ta-go, ta có

BB '  52  32  25  9  16 4cm
Diện tích tồn phần của hình lăng trụ là :

1
Stp S xq  2 S d (5  5  6).4  2( .4.6)
2
2
Stp 64  24 88cm
Bài tập mẫu 7 : Cho lăng trụ đứng tam giác ABC A'B'C' có đáy
ABC là tam giác vuông cân tại B với BA = BC = a ,biết A'B hợp với
đáy ABC một góc 600 . Tính thể tích lăng trụ.

Hướng dẫn giải
Ta có A 'A  (ABC)  A 'A  AB& AB là hình chiếu của A'B trên đáy ABC


o
và ABA ' 60

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 208


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Trong ABA' ta có

 AA ' AB.tan 600 a 3

SABC

1
a2
BA.BC 
2
= 2

a3 3
Vậy V = SABC.AA' = 2
Bài tập mẫu 8 : Cho hình lăng trụ có đáy là hình vng cạnh a.
Tính chiều cao (theo a) của hình lăng trụ, biết diện tích xung quanh
bằng diện tích tồn phần.

Hướng dẫn giải
Diện tích xung quanh hình trụ

S xq 2(a  a).h

(cm)

Stp S xq  2S d 2(a  a ).h  2a.a
Diện tích tồn phần của hình trụ

 Stp 4ah  2a 2 2a(2h  a)

1
S xq  Stp
2

Theo đề ta có
1
4ah  2a ( a  2h)
2
Hay

 4h a  2h
 2h a  h 

a
2

a
Vậy chiều cao của hình trụ là 2 (cm)
Nguyễn Quốc Tuấn (Tơng biên tâp cua Xuctu.com)

Trang số 209


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Bài tập mẫu 9 : Tính
diện tích tồn phần
(tổng diện tích các
mặt) và thể tích của
hình sau

Hướng dẫn giải
* Tính diện tích tồn phần hình lăng trụ HFG.JIK
2

2
Độ dài đường chéo của tam giác đáy là JK HG  3  4  25 5cm

1
S HFG S JIK  3.4 6cm 2
2
Diện tích tam giác đáy
Diện tích tồn phần hình lăng trụ HFG.JIK

 34 5
2
Stp1 S xq  2S day 2 
 .3  2.6 48cm
2


* Tính diện tích tồn phần của hình hộp chữ nhật ABCD.EFII’

Stp 2 S xq  2S d 2(1  3).5  2.1.3 46cm 2
2
* S JIFH 3.3 9cm

* Diện tích tồn phần của hình đã cho là

Stp Stp1  Stp 2  S JIFH 48  46  9 85cm 2
3
 Thể tích hình lăng trụ V1 S d .h 6.3 18cm

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 210


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018
3
 Thể tích hình hộp chữ nhật V2 S d .h 3.5 15cm
3
 Thể tích của hình đã cho là V V1  V2 18  15 33cm
Bài tập mẫu 10 :

Cho hình lăng trụ đứng tam giác
ABC.A’B’C’ có đáy là tam giác ABC cân
tại A có các kích thước như hình vẽ.
Tính thể tích của hình lăng trụ.

Hướng dẫn giải
Chiều cao của tam giác đáy

h '  133  52  169  25
h '  144 12cm
1
1
S  h '.BC  .12.10 60cm 2
2
2
Diện tích tam giác ABC là
3
Thể tích của hình lăng trụ ABC.A’B’C’ là V Sd .h 60.12 720cm

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 211


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Bài tập mẫu 11 : Một bình thủy tinh
hình lăng trụ đứng ABC.A’B’C’, đáy là
tam giác cân ABC có kích thước như
hình vẽ. Mực nước hiện tại trong bình

2
bằng 3 chiều cao của lăng trụ. Bây
giờ ta đậy bình lại và lật đứng lên sao
cho mặt (BCC’B’) là mặt đáy. Tính
chiều cao của mực nước khi đó.
Hướng dẫn giải
Chiều cao của tam giác đáy

h '  133  52  169  25
h '  144 12cm
1
1
S  h '.BC  .12.10 60cm 2
2
2
Diện tích tam giác ABC là

2
V 60. .12 480cm3

3
Thể tích nước hiện tại trong hình lăng trụ là
2
Nếu chọn đáy là (BCC’B’) thì S d 10.12 120cm

h' 
Chiều cao mực nước mới là

V 480

 h ' 4cm
S d 120

Vậy chiều cao mực nước mới là 4cm.
Bạn vừa xem xong phần miễn phí trong bộ sách cùng tên của thầy giáo Nguyễn
Quốc Tuấn. Để học những phần còn lại vui lòng mua trọn bộ sách của chúng tôi để
lĩnh hội được tất cả những kiến thức và Phương pháp mới nhất

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 212


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

TRON BÔ SACH THAM KHAO TOAN 8 MƠI NHÂT
Năm học 2018-2019

Bô phận ban hang:

0918.972.605

Đăt mua tai: />Xem thêm nhiều sach tai: />Hổ trợ giải đap: fb/quoctuansp

+ Bộ sach mới nhất gồm 4 quyển:
+ Phương phap giải toan từ cơ bản đến nâng cao đai số 8 tập 1
+ Phương phap giải toan từ cơ bản đến nâng cao đai số 8 tập 2
+ Phương phap giải toan từ cơ bản đến nâng cao hình học 8 tập 1
+ Phương phap giải toan từ cơ bản đến nâng cao hình học 8 tập 2
Liên hệ với chúng tôi theo các kênh liên lạc trên. Tham khảo và đọc thử tại:
/>
Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 213


Phương pháp giải toán từ cơ bản đến nâng cao Hình học 8-Chương 4: Hình lăng trụ đứng- chóp đều***Quý II-2018

Nguyễn Quốc Tuấn (Tông biên tâp cua Xuctu.com)

Trang số 214