Gui Kim Ngoc bai hinh

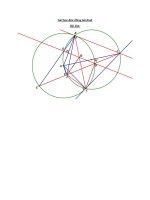
Gọi M, N là trung điểm của các cạnh BC và CD của tứ giác ABCD.
Chứng minh: (AM + AN)2 > 2.SABCD

Ta có:
S(AMC)=1/2.S(ABC)
S(ANC)=1/2S(ADC)
 S(ANCM)=S(ABCD)/2
Vì MN là đường trung bình => IC=GH S(ANCM)<2S(ANM)<= AN.AM
Suy ra
AN.AM> S(ABCD)/2
 4AN.AM> 2S(ABCD)
Mặt khác (AM+AN)^2>= 4AN.AM
Suy ra ĐPCM (ở đây ko có dấu bằng như đề bài nhé)
Nguyễn Đăng Khoa – THCS Lâm Thao – Lâm Thao – Phú Thọ