Advances in Lasers and Electro Optics Part 7 pptx

The Intersubband Approach to Si-based Lasers
287
from Si/SiGe cascade emitters at terahertz frequencies,” Applied Physics Letters 81,
(2002) 1543-1545.
[56] R. Bates, S. A. Lynch, D. J. Paul, Z. Ikonic, R. W. Kelsall, P. Harrison, S. L. Liew, D. J.
Norris, A. G. Cullis, W. R. Tribe, and D. D. Arnone, “Interwell intersubband
electroluminescence from Si/SiGe quantum cascade emitters,” Applied Physics
Letters 83, (2003) 4092-4094.
[57] J. Faist, M. Beck, T. Aellen, and E. Gini, “Quantum-cascade lasers based on a bound-to-
continuum transition,” Applied Physics Letters 78, (2001) 147-149.
[58] G. Scalar, et al “Far infrared (ߣ؆ͺ͹Ǎm) bound-to-continuum quantum-cascade lasers
operating up to 90K,” Applied Physics Letters 82, (2003) 3165-3167.
[59] L. Diehl, S. Mentese, E. Müller,, D. Grützmacher, H. Sigg, U. Gennser, I. Sagnes, Y.
Campiedelli, O. Kermarrec, D. Bensahel, and J. Faist, “Electroluminescence from
strain-compensated Si
0.2
Ge
0.8
/Si quantum cascade structures based on a bound-to-
continuum transitions,” Applied Physics Letters 81, (2002) 4700-4702.
[60] D. J. Paul, G. Matmon, L. Lever, Z. Ikoniþ, R. W. Kelsall, D. Chrastina, G. Isella, and H.
von Känel, “Si/SiGe bound-to-continuum quantum cascade terahertz emitters,”
Proceedings of SPIE 6996, (2008) 69961C.
[61] L. Lever, A. Valavanis, Z. Ikoniþ, and R. W. Kelsall, “Simulated [111] Si-SiGe THz
quantum cascade laser,” Applied Physics Letters 92, (2008) 021124.
[62] K. Driscoll and R. Paiella, “Silicon-based injection lasers using electrical intersubband
transitions in the L-valleys,” Applied Physics Letters 89, (2006) 191110.
[63] R. A. Soref and C. H. Perry, “Predicted band gap of the new semiconductor SiGeSn,”
Journal of Applied Physics 69, (1991) 539-541.
[64] D. W. Jenkins and J. D. Dow, “Electronic properties of metastable Ge
x

Sn
1-x
alloys,”
Physical Review B 36, (1987) 7994-8000.
[65] G. He and H. A. Atwater, “Interband Transitions in Sn
x
Ge
1-x
Alloys,” Physical Review
Letters 79, (1997) 1937-1940.
[66] J. Menéndez and J. Kouvetakis, “Type-I Ge/Ge
1–x–y
Si
x
Sn
y
strained-layer heterostructures
with a direct Ge bandgap,” Applied Physics Letters 85, (2004) 1175-1177.
[67] M. Bauer, C. Ritter, P. A. Crozier, J. Ren, J. Menéndez, G. Wolf, and J. Kouvetakis,
“Synthesis of ternary SiGeSn semiconductors on Si(100) via Sn
x
Ge
1–x
buffer layers,”
Applied Physics Letters 83, (2003) 2163-2165.
[68] R. Roucka, J. Tolle, C. Cook, A. V. G. Chizmeshya, J. Kouvetakis, V. D'Costa, J.
Menendez, Zhihao D. Chen, and S. Zollner, “Versatile buffer layer architectures
based on Ge
1–x
Sn

x
alloys,” Applied Physics Letters 86, (2005) 191912.
[69] P. Aella, C. Cook, J. Tolle, S. Zollner, A. V. G. Chizmeshya, and J. Kouvetakis, “Optical
and structural properties of Si
x
Sn
y
Ge
1–x–y
alloys,” Applied Physics Letters 84, (2004)
888-890.
[70] M. A. Wistey, Y Y. Fang, J. Tolle, A. V. G. Chizmeshya, and J. Kouvetakis, “Chemical
routes to Ge/Si(100) structures for low temperature Si-based semiconductor
applications,” Applied Physics Letters 90, (2007) 082108.
[71] G. Sun, H. H. Cheng, J. Menéndez, J. B. Khurgin, and R. A. Soref, “Strain-free
Ge/GeSiSn quantum cascade lasers based on L-valley intersubband transitions,”
Applied Physics Letters 90, (2007) 251105.
[72] M. Jaros, “Simple analytic model for heterojunction band offsets,” Physical Review B 37,
(1988) 7112-7114.
287
The Intersubband Approach to Si-based Lasers
Advances in Lasers and Electro Optics
288
[73] C. G. Van de Walle, “Band lineups and deformation potentials in the model-solid
theory,” Physical Review B 39, (1989) 1871-1883.
[74] V. R. D'Costa, C. S. Cook, A. G. Birdwell, C. L. Littler, M. Canonico, S. Zollner, J.
Kouvetakis, and J. Menéndez, “Optical critical points of thin-film Ge
1–y
Sn
y

alloys: A
comparative Ge
1–y
Sn
y
/Ge
1–x
Si
x
study,” Physical Review B 73, (2006) 125207.
[75] V. R. D'Costa, C. S. Cook, J. Menéndez, J. Tolle, J. Kouvetakis, and S. Zollner,
“Transferability of optical bowing parameters between binary and ternary group-
IV alloys,” Solid State Communications 138, (2006) 309-313.
[76] J. Weber and M. I. Alonso, “Near-band-gap photoluminescence of Si-Ge alloys,” Physical
Review B 40, (1989) 5683-5693.
[77] M. L. Cohen and T. K. Bergstresser, “Band Structures and Pseudopotential Form Factors
for Fourteen Semiconductors of the Diamond and Zinc-blende Structures,” Physical
Review 141, (1966) 789-796.
[78] B. K. Ridley, Electrons and Phonons in semiconductor Multiplayers (Cambridge University
Press, Cambridge, 1997), Chapter 1.
[79] B.S. Williams, S. Kumar, H. Callebaut, Q. Hu, and J.L. Reno,” Terahertz quantum
cascade laser at ߣ
~
100μm using metal waveguide for mode confinement,” Applied
Physics Letters 83, (2003) 2124-2126.
[80] K. Unterrainer, R. Colombelli, C. Gmachl, F. Capasso, H.Y. Hwang, A.M. Sergent, D.L.
Sivco, and A.Y. Cho, “Quantum cascade lasers with double metal-semiconductor
waveguide resonators,” Applied Physics Letters 80, (2002) 3060-3062.
[81] P. B. Johnson and R. W. Christy, “Optical Constants of the Noble Metals,” Physical
Review B 6, (1972) 4370-4379.

288
Advances in Lasers and Electro Optics
II Applications in Communications

14
Evolution of Optical Sampling
Gianluca Berrettini
1
, Antonella Bogoni
2
, Francesco Fresi
1
,
Gianluca Meloni
2
and Luca Potì
2

1
Scuola Superiore Sant’Anna, Pisa,
2
CNIT - Photonic Networks National Laboratory,
Via G. Moruzzi 1, 56124 Pisa,
Italy
1. Introduction
The need of direct measure and monitoring of ultra-fast signal in the time domain is rapidly
increasing, being of interest in a large number of applications such as ultra-fast
communication, biophotonics, sensing, large systems synchronization, dynamic
characterization and testing of new materials. In particular in the telecommunication field
optical sampling can been exploited for high bit rate waveform and eye diagram

measurements, time resolved state of polarization monitoring, and investigation of fiber
transmission impairments.
Microwave digital sampling techniques are evolved into powerful tools for resolving signals
up to 100 GHz (Agoston et al., 2003), but electronic bandwidth limitations still remain.
Nowadays digital sampling operations in the optical domain look like an effective
alternative solution for increasing the sampling bandwidth and resolve signals up to
640 Gb/s and beyond. In the optical sampling techniques system, the optical signal is
sampled in the optical domain by an optical sampling gate. Only then, the resulting samples
are converted to an electrical signal and detected. In this case the need for high bandwidth
electronics is circumvented and the bandwidth of the measurement instrument is only
limited by the optical sampling gate.
Up to now different kinds of optical sampling techniques have been proposed in order to
study the behavior of ultra-fast optical signals. Many solutions implement a synchronous
sampling that may enable low jitter, high resolution and high accuracy. This technique
needs a clock recovery system to synchronize the optical sampling pulses to the signal
under test; however, when the data rate or repetition rate of the analyzed signal is very
high, the development of the synchronization circuitry can be very critical and expensive. In
particular, in case of repetition rates beyond 100 GHz, some all-optical clock recovery
solutions have to be adopted (Yamamoto et al., 2001; Tong et al., 2000; Uhua et al., 2003), but
which are still far from being technologically consolidated. Other optical sampling schemes
carry out an asynchronous sampling exploiting sophisticated electronics for the generation
of a sampling gate (Shake et al., 2003a). Optical asynchronous sampling has been
successfully demonstrated for signal up to 160 Gbit/s in (Westlund et al., 2005 a,b), where
the capability of the optical sampler to estimate the Q value and the performances of the
Advances in Lasers and Electro Optics

290
exploited nonlinearity are investigated, confirming the high potentialities of an asynchronous
sampling technique.
Finally, quasi-synchronous optical sampling has been demonstrated for 640 Gb/s optical

time division multiplexing (OTDM) signals without data-post processing (Fresi et al., 2008).
Independently on the sampling technique, the optical sampling operation requires a
nonlinear interaction between the signal to be resolved and an ultra-short pulse train that
act as sampling signal. Such nonlinear process can be generated in different nonlinear
elements as highly non linear fiber (HNLF) (Malacarne et al., 2007; Watanabe et al., 2004;
Schmidt et al., 2002a), nonlinear crystals and waveguides (Nogiwa et al., 2000; Takara et al.,
1996a; Kawanishi et al., 2001) or semiconductor devices (Maguire et al., 2005; Shirane et al.,
2000). Fibers, crystals and waveguides may enable ultra-fast dynamics and high efficiency,
while semiconductor devices could reduce the power consumption.
2. Digital sampling operation
In contrast to an analog oscilloscope, a sampling oscilloscope acquires the waveform as a
series of samples, and stores these samples until it accumulates enough samples to describe
a waveform. Conventional electronic digital sampling oscilloscopes use analod to digital
convertersi (ADC) to sample the signal at discrete points in time and convert the signal’s
voltage at these points into digital values called sample points. The sample clock determines
how often the ADC takes a sample. This rate is referred to as the sample rate and is
expressed in samples per second (S/s). Although there are a number of different
implementations of sampling technology, today’s digital oscilloscopes utilize two basic
sampling methods: real-time sampling and equivalent-time sampling. Equivalent-time
sampling can be divided further, into two subcategories: random and sequential. Each
method has distinct advantages, depending on the kind of measurements being made.
Real-time sampling is ideal for signals whose frequency range is less than half the
oscilloscope’s maximum sample rate. Here, the oscilloscope can acquire more than enough
points in one “sweep” of the waveform to construct an accurate picture. Real-time sampling
is the only way to capture fast, single-shot, transient signals with a digital oscilloscope.
High-frequency transient events occur only once, and must be sampled in the same time
frame that they occur. If the sample rate isn’t fast enough, high-frequency components can
“fold down” into a lower frequency, causing aliasing in the display. In addition, real-time
sampling is further complicated by the high-speed memory required to store the waveform
once it is digitized.

Equivalent-time sampling can be used to accurately acquire signals whose frequency
exceeds half the oscilloscope’s sample rate. When measuring high-frequency signals, the
oscilloscope may not be able to collect enough samples in one sweep. Equivalent time
digitizers (samplers) take advantage of the fact that most naturally occurring and man-made
events are repetitive. Equivalent-time sampling constructs a picture of a repetitive signal by
capturing a little bit of information from each repetition. The waveform slowly builds up
like a string of lights, illuminating one-by-one. This allows the oscilloscope to accurately
capture signals whose frequency components are much higher than the oscilloscope’s
sample rate. There are two types of equivalent-time sampling methods: random and
sequential. Each one has its advantages. Random equivalent-time digitizers (samplers)
utilize an internal clock that runs asynchronously with respect to the input signal and the
Evolution of Optical Sampling

291
signal trigger. Samples are taken continuously, independent of the trigger position, and are
displayed based on the time difference between the sample and the trigger. Although
samples are taken sequentially in time, they are random with respect to the trigger – hence
the name “random” equivalent-time sampling. Sequential equivalent-time sampling
provides much greater time resolution and accuracy. It acquires one sample per trigger,
independent of the time/div setting, or sweep speed. When a trigger is detected, a sample is
taken after a very short, but well-defined, delay. When the next trigger occurs, a small time
increment “t” is added to this delay and the digitizer takes another sample. This process is
repeated many times, with “t” added to each previous acquisition, until the time window is
filled. Sample points appear from left to right in sequence along the waveform when
displayed on the oscilloscope screen. Since with sequential sampling the sample is taken
after the trigger level is detected, the trigger point cannot be displayed without a variable
delay line, which may, in turn, reduce the bandwidth of the instrument. Both require that
the input signal be repetitive (Tektronix, 2001).
3. Optical sampling
The optical sampling is a novel method to perform time-resolved measurements of optical

data signals at high bit rates with a bandwidth that cannot be reached by conventional
photodetectors and oscilloscopes (Schmidt-Langhorst & Weber, 2005). Fig. 1 explains the
principle of optical sampling. The upper part of the figure shows an optical data signal with
RZ modulation format as example. The data signal is a concatenation of optical data bits,
each within a bit slot of 6.25 ps corresponding to a bit rate of 160 Gbit/s. This optical data
signal is passed through an optical gate. The gate is closed by default, i.e. it does not
transmit the data signal for most of the time except for ultra short periods of time. The
period of time for which the gate transmits the data signal is called “gating window”. If the
width of the gating window is shorter than the bit duration, as shown in Fig. 1, only a
fraction of the optical data bit is sliced out. This fraction is called “optical sample”. The
optical sample is determined by the instantaneous amplitude of the data bit at the sampling
time. Ideally, the sampling gate should exhibit a linear transfer function making the
amplitude of the optical sample directly proportional to the instantaneous power of the data
signal at the sampling time.

Sampling Period
Pulsewidth
(i.e. 1 ps)
Slow
Photodetector
Data signal
Sampling
gate
Optical
sample
Electrical
sample
Bit slot
(i.e. 6.25 ps)

Fig. 1. Operating principle of optical digital sampling
Advances in Lasers and Electro Optics

292
In order to avoid high-speed electronic signal processing for the detection of the optical
samples, it is useful to operate the sampling gate with a modest repetition frequency, then
only equivalent-time sampling techniques are considered. At the output of the detector, the
“electrical sample” appears broadened in time due to the low bandwidth of the detector, but
still generates a photocurrent that is proportional to the instantaneous optical power of the
optical data bit at the sampling time. After a transimpedance amplifier, the peak voltage V
p

of each electrical sample is measured by an ADC. The eye diagram of the optical data signal
is obtained from the measured V
p
-values if the corresponding sampling times are known.
The optical sampling technique described in Fig. 1 allows to visualize the eye diagram of
any data signal that has been encoded by an amplitude modulation format. In the case of a
phase modulation format, this sampling technique will not distinguish between logical
mark and space levels in the eye diagram. Up to now, only few work has been reported on
the monitoring of phase modulated optical data signals. In a simple approach, a phase
demodulator was incorporated in an optical sampling system (Schmidt-Langhorst et al.,
2005). The demodulator converts the phase modulated data signal into an amplitude
modulated data signal before the sampling operation. Another approach is the
measurement of constellation diagrams of a phase modulated data signal (Dorrer et al.,
2004). Such diagrams represent the amplitude and phase information of the data signal in
the complex plane. Moreover FROG technique can be exploited to acquire signal amplitude
and phase information.
For sake of shortness we consider here optical sampling techniques for solving only the
signal amplitude.

3.1 Sampling gate generation
The generation of the sampling gate is the main subsystem of an optical sampling
oscilloscope. It can be performed exploiting nonlinear interactions between the signal to be
resolved and an ultra-short pulse train that acts as sampling signal.
The most important parameters of the sampling pulse source are the timing jitter and the
pulse width. The timing jitter of the pulse source determines the timing jitter of the whole
sampling system, whereas the pulse width limits the temporal resolution of the sampling
system. As a rough estimate, a timing jitter of less than 300 fs and a pulse width of about
1 ps are necessary to measure a 160 Gbit/s optical eye diagram. Another important
parameter is the repetition frequency of the pulse source. The required sampling rate is
typically a few hundred MHz, since the O/E detection frequency in the optical sampling
systems is limited to a few hundred MHz.
Different techniques can be considered to generate the sampling signal. Directly modulated,
gain-switched laser diodes exhibit high jitter and could require additional compression
stage (Ohta et al., 2000). Distributed FeedBack DFB lasers in continuous wave mode
cascaded by electroabsorption modulators (EAM) to carve sampling pulses generate broad
pulses due to the limited bandwidth of the available EAM’s (Otani et al., 1999). Therefore,
the pulses had to be compressed for the application as sampling pulses. Hybrid mode-
locked semiconductor laser diode offers the potential of monolithic integration but the
repetition rate has to be usually reduced using external LiNbO
3
amplitude modulator
(Schmidt et al., 2002b). Mode-locked Erbium doped fiber lasers are the most widely used
sampling pulse sources due to their very low jitter. Also in this case the pulse repetition
frequency has to be externally reduced to a few hundred MHz by gating the pulse train with
a LiNbO
3
modulator (Li et al., 2004; Li et al., 2001; Takara et al., 1996a,b).
Evolution of Optical Sampling

293
The most common techniques used to produce optical nonlinear interaction for the
generation of the sampling gate exploit optical fiber, crystals and waveguides or
semiconductor devices. A summary of all nonlinear effects used for optical sampling is
reported in Tab. 1.

SFG
SHF/DFG
Crystals and waveguides
FWM in SOA
UNI
GT-UNI
EAM
TPA
Semiconductor devices
FWM
XPM induced wavelength shifting
NOLM
Kerr gate
Optical fiber
Nonlinear effectMaterial
SFG
SHF/DFG
Crystals and waveguides
FWM in SOA
UNI
GT-UNI
EAM
TPA
Semiconductor devices

FWM
XPM induced wavelength shifting
NOLM
Kerr gate
Optical fiber
Nonlinear effectMaterial

Table 1. Summary of nonnlinear effects and nonlinear media exploited for optical sampling.
3.1.1 Optical fiber
The ultra-fast Kerr nonlinearity of the optical fiber provides short gating windows
comparable to those of the crystal based gates. The exploited nonlinear processes include
four wave mixing (FWM) (Miyazaki & Kubota, 2003), parametric amplification (Li et al.,
2001) and cross phase modulation (XPM) induced wavelength shifting (Li et al., 2004). As
the efficiency of these processes is rather small, high peak powers were needed for
switching. The operational wavelength range of FWM-based all-optical sampling is usually
limited by the phase-matching condition. Moreover, in order to cover the whole usable
signal wavelength band, the wavelength of the sampling pulses should be set far away from
that of the signal, which results in poorer temporal resolution, due to the relatively large
walkoff between the signal and sampling pulses. Compared to FWM-based schemes, XPM-
based optical sampling can place the sampling pulses just outside the usable signal
wavelength region, therefore, the whole usable signal wavelength band can be covered,
while the temporal resolution at the order of the sampling pulse width is maintained.
However, XPM-based schemes exploiting narrow filtering are more sensitive to the chirp of
the data signal, which can introduce some distortions.
Interferometric gates based on highly nonlinear fibers need less peak power of the sampling
pulses to achieve gating windows with high on-off contrast. Examples include the nonlinear
optical loop mirror (NOLM) (Schmidt et al., 2002a) and the so-called “Kerr gate” (Schmidt-
Langhorst et al, 2002). The latter was recently combined with the effect of parametric
amplification in (Watanabe et al., 2004).
3.1.2 Crystals and waveguides

For the purpose of obtaining higher sensitivity and higher temporal resolution, some
sampling systems employ sum frequency generation (SFG) in the nonlinear crystals
(Yamada et al., 2002), periodically poled Lithiumniobate (Yamada et al., 2004; Nogiwa et al.,
2000; Ohta et al., 2001) or the organic crystal (Takara et al., 1996b). While these gates provide
very short optical gating windows (<1 ps), their main drawback is the required high peak
Advances in Lasers and Electro Optics

294
power, which is necessary to generate a sufficient amplitude of the frequency converted
signal. In general, the use of periodically poled material reduces the power requirements as
long interaction lengths without loss of phase matching can be achieved. Moreover, if the
SFG process is performed with sampling pulses at about 780 nm, the generated light has a
wavelength of about 520 nm and can be easily separated from the sampling pulse light as
was shown in (Jungerman et al., 2002). In addition to the SFG process, the cascaded χ(2)
processes of second harmonic generation and difference frequency generation (SHG/DFG)
have been used as well (Kawanishi et al., 2001).
3.1.3 Nonlinear effects in semiconductor devices
The resonant nonlinearity of a semiconductor optical amplifier (SOA) requires less optical
power for the gating pulses (Shirane et al., 2000). Devices based on conventional FWM in
SOA’s suffer from the fact that the conversion efficiency and the signal-to-background ratio
drop rapidly for wavelength detunings between control and data wave larger than some
nanometers. So, for the sake of high conversion efficiency or high FWM output power (i.e.,
high optical power of the FWM signal at the SOA output), the signal has to be kept within
the gain wavelength region of the SOA. Hence, the data signal will contribute to gain
saturation in the SOA. This is unwanted in sampling applications, where a strict linearity of
the FWM output power versus the data input power is required for a quantitative
assessment of the shape of the data pulses. Additionally, there is a strong contribution of
amplified spontaneous emission (ASE) noise to the converted FWM signal, since the data is
within the spectral range of the ASE. A higher switching efficiency is obtained by XPM in an
SOA in combination with an interferometric configuration as gate. A promising gate of this

kind is the so called “ultrafast nonlinear interferometer” (UNI), which was used in (Kang &
Dreyer, 2003). However, this gate suffered from the amplified spontaneous emission (ASE)
of the SOA. An EAM with sophisticated synchronization and driving electronics was
additionally needed to suppress the ASE after the UNI gate. In a more advanced scheme, the
superior gating performance of interferometric optical gates was combined with the so
called gain-transparent operation of an SOA. In this operation of the SOA, the wavelength of
the data signal is outside the gain spectrum of the SOA. Therefore it does not suffer from
ASE degradation. Moreover, the gain-transparent SOA gate exhibits a linear transfer
function for the data signal. This is in contrast to the conventional SOA gates, which show a
strong saturation. Finally, the gain-transparent operation enables a wide wavelength
acceptance range of the gate. The gain-transparent configuration was used in the “gain-
transparent ultrafast-nonlinear interferometer” (GT-UNI) sampling gate in (Schmidt et al.,
2002b). For the sake of completeness it should be mentioned also that even EAM have been
used recently as sampling gates in optical sampling experiments. Since the width of the
gating window, which can be achieved with an EAM, is rather large (about 5 ps), these gates
could be applied only to bit rates up to 40 Gbit/s (Shake et al., 2003b). Recently though, eye
diagrams even at a bit rate of 160 Gbit/s were measured using a double-pass EAM
configuration (Kang & Dorrer, 2003).
3.1.4 Two photon absorption (TPA) in semiconductor devices:
The phenomenon of TPA is a nonlinear optical-to-electrical conversion process where two
photons are absorbed in the generation of a single electron-hole pair (Folliot, 2002). It occurs
when photons of energy E
ph
are incident on the active area of a semiconductor device with a
Evolution of Optical Sampling

295
bandgap exceeding E
ph
but less than 2E

ph
. The generated photocurrent is proportional to the
square of the intensity, and this nonlinear response enables the use of TPA for optical
sampling. As TPA is an instantaneous optical nonlinearity, it may be used for all-optical
high-speed sampling in photonic systems. The main difficulty with using TPA for high-
speed optical sampling is its inherent inefficiency, which means that such systems either
require high optical intensities or very long detectors, making them unsuitable for practical
telecommunications applications. One possible way to overcome this efficiency problem is
to employ a semiconductor microcavity (Krug et al., 2004), which should significantly
enhance the TPA response of the device, and enable the implementation of a practical
sampling element for high-speed optical systems.
3.2 Optical sampling parameters
An optical sampling system is characterized by the following main parameters:
Temporal resolution
It is typically specified by the full-width at half maximum (FWHM) of the sampling system
gating window The temporal resolution is equivalent to the bandwidth of the sampling
system.
Timing jitter
The timing jitter is typically specified as root-mean-square (RMS) jitter.
Wavelength range
It is usually specified as 3 dB bandwidth and defines the range of wavelengths, which a data
signal can have to be accepted by the sampling system.
Sensitivity
There is no common definition of this parameter with respect to optical sampling systems.
Some authors use the product of the average sampling pulse power and the peak signal
power. Another definition of the sensitivity uses the peak power of the signal pulses, which
is required to achieve a certain displayed signal-to-noise ratio (Yamada et al., 2002) or in
case of SFG the well know conversion efficiency parameter.
Dynamic range
It is the power range in which the signal under investigation must fall.

Polarization sensitivity
It describes the amount by which the amplitude of the generated samples varies, when the
polarization of the signal under investigation changes.
Applicable bit rate
It is the range of bit rate, at which a particular sampling system was able to display an open
eye diagram.
3.3 Synchronous, quasi-synchronous and asynchronous optical sampling
As reported in Fig. 2, in the synchronous sampling configuration, the sampling gate is
opened synchronous to the optical data signal but with an increasing time delay in order to
scan over the complete bit slot. Thus a technique is needed for the synchronization of the
sampling gate to the optical data signal under investigation. This function is performed by
an optical clock recovery (CR).
The quasi-synchronous scheme requires an additional subsystem to impose a frequency
mismatch between the repetition rates of the signal under test and the sampling signal. In
this way a complete scan of long signal time intervals can be directly achieved. In the
asynchronous sampling configuration, the clock processing is omitted and the sampling
Advances in Lasers and Electro Optics

296
process is performed at random times. The sampling times are derived from an arrival time
measurement of the sampling pulses themselves. As compared to the synchronous sampling
configuration, the random sampling configuration requires less components as there is no
need for a clock processing circuitry. However, it requires the use of a special O/E-detector,
which performs the arrival time measurement of the sampling pulses with high temporal
accuracy, as an error in the arrival time measurement directly translates into timing jitter of
the sampling system.

CR PLL
CR
Input signal

Sampling signal
VODL
50 Hz
Input signal
Sampling signal
Pre-scaled
f
in
+Δf
synchronous
quasi-synchronous
Input signal
~10 MHz
MLFL
asynchronous
Electrical
processing

Fig. 2. Scheme of a synchronous (top), quasi-synchronous (center), and asynchronous
(bottom) optical digital sampling.
In the following sections the implementation of synchronous, quasi-synchronous and
asynchronous optical samplers exploiting optical fiber nonlinearities is presented.
4. Synchronous optical sampler based on Kerr nonlinearities
In the synchronous sampling technique, the sampling signal has to be synchronized with the
signal to be sampled, thus requiring some kind of synchronization circuitry. The proposed
scheme is based on the nonlinear effects in a highly non linear fibre. The accuracy of this
sampling technique strongly depends on the non linear phenomenon efficiency by means of
the non linear coefficient, and the fibre length. Nowadays, HNLFs with a flat chromatic
dispersion curve and high birefringence are available, thus avoiding efficiency reduction
caused by signals walk-off and polarization fluctuations.

The principle of the implemented optical sampler is the same as for commercial electrical
sampling oscilloscopes. A schematic about the sampling principle is displayed in Fig. 3. In
an ideal sampling, the signal to be measured S(t), is multiplied in the time domain by a delta
signal
δ
(t
0
). The result of the interaction between the two signals, is the power of S(t)
measured for t = t
0
, that is S(t
0
). By continuously time shifting the delta signal over S(t), it is
Evolution of Optical Sampling

297
possible to measure the signal power at different instants t
i
. Such samples represent a replica
for the signal under measure. In Fig. 3(a), the principle scheme about the ideal signal
sampling is shown. In a real measurement, the sampling signal will have necessarily a non-
zero time duration (Fig. 3(b)); thus consisting in a unavoidable sampling error.


Fig. 3. Ideal operating sampling principle (a), and the real sampling of a periodic signal (b).
If the signal to be sampled is periodic with a period T, it is possible to sample it using
another periodic signal whose period T
S
is a multiple of T (T
S

= mT). The accuracy of the
sampling process is expressed by:

1/
00
0
() ()( )
S
f
S
St f StPt t dt
ε
=− −
∫
(4.1)
where P(t) is the sampling signal, and f
S
is the sampling frequency ( f
S
= 1/T
S
). The previous
technique, can be implemented exploiting whatever effect between S(t) and P(t), that gives a
well known function of the signal power. A non linear effect that can be exploited is the
Four Wave Mixing (FWM). The FWM non linear Kerr effect takes place when two or more
powerful signals at different wavelength propagate through a non linear medium. When
two optical signal P(t) with a wavelength
λ
i
, and S(t) with a wavelength

λ
j
, are transmitted
through a non linear device, new components (called conjugate components) are generated
with wavelengths related to the difference
Δλ
= |
λ
i
-
λ
j
|. In Fig. 4 it is displayed the FWM
effect in the frequency domain. The conjugate component at the wavelength
λ
i
-
Δλ
has a
power proportional to S(t), and then it can be filtered out and detected, measuring the
original signal. The key parameters in this technique are the non linear coefficient g of the
used non linear medium, and the power of the signals.


Fig. 4. FWM effect taking place when two powerful signals P(t) and S(t) are launched
through a non linear device.
The FWM efficiency is given by:
η =
(
γ

PL)
2
(4.2)
where L is the fibre length, and P is the peak power of the sampling signal. The temporal
resolution of the fibre based all optical sampler is determined by a combination of the
Advances in Lasers and Electro Optics

298
sampling pulse width, and the temporal walk-off due to the chromatic dispersion between
the sampling pulses and the signal during the sampling process. Afterwards, in order to
obtain a good resolution, it is necessary to sample the signal with short sampling pulses, and
to have a low value of dispersion slope. In a first implementation of the sampler, a fibre
based active mode locking source has been used in order to generate the sampling pulses,
with a repetition frequency of 10 GHz and a pulse width of about 4 ps. The laser source
output has been directly used to sample a nonreturn-to-zero (NRZ) modulated signal. As
further measure, a return to zero (RZ) signal was sampled, verifying the time resolution of
the scheme. For the RZ signal sampling, a higher time resolution was obtained compressing
the ML source pulses down to about 1 ps, and using that as sampling signal. For both the
measures, the FWM component generated during the transmission was filtered out by
means of an optical filter (dotted line in Fig. 4).


Fig. 5. Setup of the implemented synchronous optical sampler.
In Fig. 5, the setup of the implemented synchronous optical sampler is shown. In order to
validate the functioning of the scheme, a NRZ signal, obtained modulating a 1550 nm
Continuous Wave (CW), was sampled. For the experiment, a 400 m long HNLF with
γ
= 10W
-1
Km

-1
and slope S = 0.3 ps/nm
2
/Km, was used as non linear medium. The NRZ signal
was coupled together with the ML laser source output, whose wavelength was
λ
s
= 1557 nm. The power and the polarization state of both signal and pump (sampling
signal) was optimized by means of Erbium Doped Optical Amplifiers and polarization
controllers respectively. A Piezo-electric Optical Delay Line (P-ODL) driven by a 100 MHz
electric triangular waveform, was used in order to shift the sampling pulses with respect to
the signal. In such a way it is possible to visualize the behaviour of the mean power at the
output of the optical filter with a refreshing time of the order of 100 ms. A 150 MHz
photodiode (PD) and a 500 MHz oscilloscope triggered with the 100 MHz triangular
waveform, was used to display the sampling result. An alternate modulation pattern was
used, whereas the sampling signal frequency was fixed to 5 GHz in order to have the same
periodicity as the signal under test. The mean power measured by changing the sampling
pulses time position, directly gives the NRZ signal shape. In Figure 6 the results about the
sampling of the NRZ signal are reported. The signal was opportunely pre-distorted in order
to evaluate the sampler accuracy. In order to demonstrate the high resolution that can be
obtained exploiting the Kerr non linearities (i.e. FWM), the ML laser source pulses was
resolved. In this measure, the setup was slightly different from the scheme of Fig. 5. In
Evolution of Optical Sampling

299
particular, the ML pulsed signal was split, compressed and used also to generate the
sampling signal. The compression was made by means of a higher order soliton compressor,
obtaining pulses of about 350 fs. In Fig. 7 the scheme of the compressor and the obtained
compressed optical pulse autocorrelation trace are displayed.

Fig. 6. comparison between the implemented optical sampler and the commercial
oscilloscope measures.

Fig. 7. Scheme of the higher order soliton compressor (left), and autocorrelation trace of the
obtained compressed pulse (right).
In Fig. 8, the 10 GHz ML sampled pulses (left) and the comparison between the
autocorrelation trace measured by means of a commercial autocorrelator (right) are
reported.


Fig. 8. 10 GHz sampled signal (left), and comparison between the autocorrelation traces
(right).
Another experiment was made in order to evaluate the sampler resolution. The signal to be
measured was obtained time-multiplying the ML laser source output with an all optical
Advances in Lasers and Electro Optics

300
multiplexer realized with the split-and-delay technique. In Fig. 9 are reported the results of
the 80 GHz signal sampling.
Finally, in order to qualitatively estimate the maximum resolution of the implemented
optical sampler, the signal to be sampled was distorted changing the power level in the
compressor, obtaining an asymmetric and irregular optical pulse. This way, sub-picosecond
dynamics was obtained and measured by the sampler, verifying its functioning for the
measure of ultra short signals. In Fig. 10 the result about the sampling of the distorted pulse
is shown.


Fig. 9. 80 GHz sampled signal (left), and comparison between the autocorrelation traces
(right).

Fig. 10. Intensity trace of the distorted sampled pulse.
A scheme similar to the one described was implemented exploiting the non linear effect of
cross phase modulation (XPM). In particular, the exploited effect was the XPM-induced
polarization rotation. In Fig. 11 the setup of the optical sampler is reported. As in the
previous scheme, an ultra short pump with high peak power interacts with the signal while
propagating in the non linear fibre. In this optical sampler, a quasi instantaneous phase
rotation (typical response time < 50 fs) is induced by the sampling pulse on the signal
portion superimposed to the pump.
By means of a polarization controller and a polarizer at the output of the non linear element,
it is possible to extract the portion of the signal time overlapped to the pump. This power
portion can be then measured by using a narrow bandwidth photoreceiver. If the pump is
short enough, that measured power can be approximated with the instantaneous signal
power. As described before, by shifting the pump with respect to the signal its time shape

Evolution of Optical Sampling

301

Fig. 11. Experimental setup of the synchronous sampler based on XPM-induced polarization
rotation in 1 m of Bi
2
O
3
fibre.
can be measured. One difference with respect to the previous scheme, is that in this case, the
non linear medium is a Bismuth Oxide fibre (Bi
2
O
3

) with a very high non linear coefficient
γ
= 1250 W
-1
Km
-1
, a total attenuation a = 6 dB and an accumulated chromatic dispersion
D
t
= - 0.33 ps/nm at a wavelength
λ
= 1550 nm. Such a high non liner coefficient permits to
strongly decrease the fibre length down to L = 1.08 m. The use of short fibre spans reduces at
the same time the polarization fluctuation and the scheme footprint, making the system
more stable and compact. The sampling pulses was obtained by means of soliton
compression on the ML sources and the signal under test was obtained by λ-converting the
same ML laser. The wavelength conversion was made exploiting FWM in 250 m of HNLF.
Moreover, the signal was coupled with the pump with a 45°-rotated polarization state in
order to obtain maximum XPM-induced polarization rotation. Fig. 12 (left) shows the
optically sampled pulse shape, whose pulse width of 6 ps was measured. In order to verify
the accuracy of the implemented scheme, the obtained sampled trace autocorrelation was
compared with the results supplied by a commercial autocorrelator obtaining a very good
agreement between the traces, and verifying a picosecond resolution of the sampler (see
Fig. 12 (right)).


Fig. 12. 6 ps soliton pulse measured by the optical sampler (left) and comparison between
the autocorrelation traces supplied by a commercial autocorrelator and the processed data
measured by the implemented optical sampler (right).
Advances in Lasers and Electro Optics

302
5. Asynchronous optical sampling
An important issue of synchronous sampling technique is that it requires a synchronization
between the sampling signal and the signal under investigation. Unfortunately, the
synchronization of fast optical signals it is not easy and it requires complex all optical
techniques and fast electronics. For this reason, it is useful an asynchronous sampling
operation. An Asynchronous all optical Sampling Oscilloscope based on FWM in HNLF
(ASOF) has been also implemented. The asynchronous solution, based on the knowledge of
the mean frequency of the signal under test, avoids the use of a clock recovery circuit, with
strong advantages in terms of complexity and cost. This kind of sampler has not only the
advantage of not requiring synchronization circuits, but also the capability of describing
both signal eye diagram and long bit sequences (several ns), thanks to the asynchronous
operation. Moreover, a sub-ps resolution can be obtained due to the exploited ultra fast non
linear Kerr effects in fiber. A short refresh time was obtained using a commercial
oscilloscope able to directly acquire and process a large amount of data. The working
principle of the implemented asynchronous sampler is shown in Fig. 13. As in the previous
schemes, the asynchronous optical sampling oscilloscope exploits the non linear interaction
between the signal under test and the sampling signal. The signal under test was periodic
with a frequency f
S
= 1/T
S
, where T
S
is its period.


Fig. 13. ASOF working principle.
The sampling frequency f

C
is not correlated to f
S
, meaning that there is no need for any fixed
relation between the two frequencies. Every pulse of the sampling signal generates a pulsed
FWM component, whose energy is proportional to the instantaneous power of the signal
under test in the corresponding interaction time. Since the frequencies of the involved
signals are not correlated, two consecutive samples do not correspond to two consecutive
instantaneous power values of the signal; on the opposite the temporal sequence of the
samples appears as shuffled sampling of the analyzed signal. Besides, the sample sequence
can be stored through an acquisition board, and then the sampled signal can be correctly
reconstructed, if the difference of the period T
S
- T
C
is known. Therefore a post processing
can be applied to the sample sequence for re-ordering the collected points and
reconstructing the original signal shape. In more details, the position of the i-th sample, with
respect to the period of the signal under test, is defined by the following equation:

0
()
SC
i
S
TT
ttModi
T
⎡
⎤

−
=+
⎢
⎥
⎣
⎦
(5.1)
Evolution of Optical Sampling

303
where t
0
is a reference initial time that can be set to zero. The samples can not be equally
spaced depending on the relationship between T
S
and T
C
, and on the acquisition time.
Consequently a mean resolution R of the ASOF can be defined as:

T
R
N
=
(5.2)
where T is the signal time interval to be resolved, and N is the number of acquired samples.
One of the most critical issue of an asynchronous sampling technique is the phase noise that
can be introduced by the sampling process. For this reason an analytical study of the phase
noise generated in the implemented scheme was made. Due to the asynchronous behavior
of the sampling operation, the introduced phase noise strongly depends on the phase noise

of the signal under test and of the sampling pulse train. For the implemented scheme, it is
possible to neglect the phase noise of the sampling pulse since its value was verified to be
one order of magnitude lower than the phase noise of the considered signal. The analysis
was made considering a sinusoidal waveform at 39.9 GHz as signal to be resolved. In this
case, being S(t) the signal under test, it can be modelled in the time domain as the sum of
two components: the first one represents the noise-free sinusoidal signal S
nf
(t), and the
second one H(t) includes all amplitude and phase noise contributions:
() () ()
nf
St S t Ht=+ (5.3)
Considering the signal electrical spectrum P(f), the noise term can be modelled as the sum of
the sinusoidal functions that represent all the components of the sideband noise of P(f):

0
() sin(2 ( ) )
M
ilow
i
Ht a f i f i
πδ
=
=+Δ+
∑
(5.4)
where the sideband noise of the electrical spectrum has been divided in M slices with a
frequency step equal to Δ
f
, while f

low
and f
high
= ( f
low
+M
Δ
f ) are the upper and lower bounds
of the noise bandwidth to be considered; a
i
is the spectral power associated to the frequency
f
i
= (f
0
+f
low
+i
Δ
f) being f
0
the carrier frequency of the signal, and δi is a random variable
uniformly distributed in the range 0÷2π accounting for the phase of the noise spectral
components. The bandwidth f
high
- f
low
, depends on the time needed for the acquisition of all
the optical samples allowing the desired resolution of the signal under test. In the
implemented scheme, all the acquisition times are shorter than 10 ms and consequently it is

possible to neglect all the noise components at frequencies lower than f
low
= 10 KHz. The
upper limit of the bandwidth to be considered was fixed to f
high
= 1 MHz, since all higher
spectral components present negligible amplitude. H(t) includes both amplitude and phase
noise, but it can be demonstrated (Von der Linde, 1986), that for f
low
≥ 10 KHz the phase
noise is dominant. Consequently all the contribution of H(t) can be assumed as phase noise,
thus making a worst case approximation. The phase noise can be estimated in terms of
timing jitter. The jitter can be extracted from the sideband noise of the signal electrical
spectrum according to:

0
1
,
2
s
b
low high
C
P
Jf f
f
P
π
⎡⎤
=

⎣⎦
(5.5)
Advances in Lasers and Electro Optics

304
where P
C
is the mean power of the sinusoidal waveform S
nf
(t), and P
sb
in the integral of the
sideband of the electrical spectrum of S(t):

0
0
()
1.2
high
low
ff
sb
ff
Pf
Pdf
B
+
+
=
∫

(5.6)
As explained in the previous chapter, the factor 1.2 normalizes the filter response of the
electrical spectrum analyzer to a rectangular function, and B is the resolution bandwidth of
the electrical spectrum analyzer. In the analytical investigation, H(t) was obtained from the
experimental sideband noise of the electrical spectrum reported in Fig. 14 (left), concerning a
sinusoidal clock at 39.9 GHz.

Fig. 14. Frequency distance from signal carrier (left) and analytical time jitter of the sampled
signal as a function of the time jitter of the signal to be sampled (right).
The timing jitter of this signal, measured in the range 10 KHz ÷ 1 MHz, is equal to 70 fs. The
sampling signal was considered to be a train of ideal delta functions with a repetition rate of
500 MHz, the acquisition time was set to 1 ms, and the time interval to be measured was
fixed to 25 ps. The mean resolution can be estimated to be R = 50 fs. An analytical tool
extracts the sequence of the instantaneous powers of the signal S(t) corresponding to the
interaction times between the signal and the delta function train. The tool then calculates the
correct time position for each sample, with respect to the period of the signal to be
measured, exploiting eq. 5.1. The timing jitter of the signal measured by the asynchronous
sampling operation, could not be evaluated exploiting the previous equations since it was
obtained by a data post processing, and its electrical spectrum was not available. Therefore
the timing jitter was evaluated directly in the time domain, as it is for any commercial
oscilloscope, considering the sampled curve as the sum of an ideal curve and a random
variable with a gaussian time distribution. The timing jitter was then measured as the
standard deviation of this time distribution, evaluated at half maximum of the curve
displayed by the optical sampler. For the implemented scheme, a signal timing jitter of
156 fs was estimated, about two times higher then the timing jitter of the signal under test
(76 fs). Consequently, it is possible to assert that the phase noise introduced by the
asynchronous sampling operation does not compromise the measure of this 40 GHz signal
with a sub-ps resolution. In Fig. 14 (right) the estimated timing jitter of the signal as
visualized by the ASOF is plotted as a function of the timing jitter of the signal under test,
obtaining a clear parabolic behavior. The increasing timing jitter of the signal to be sampled,

Evolution of Optical Sampling

305
was obtained considering in all cases the sideband noise of the electrical spectrum reported
in Fig. 14(left), but with a decreasing mean power P
C
of S(t). For an input signal with a
timing jitter lower than 100 fs in the range 10 KHz÷1 MHz, the implemented asynchronous
sampler allows to describe the signal time evolution with a timing jitter lower than 200 fs.
For higher values up to 600 fs, the timing jitter of the sampled curve as displayed by the
ASOF does not exceed a value of 2 ps. Therefore this analysis has verified that the
asynchronous sampling technique, despite avoiding the clock recovery operation,
introduces a low amount of additional phase noise, allowing to measure ultra fast signal
with high accuracy. The experimental setup for the ASOF implementation is shown in
Fig. 15.

Fig. 15. ASOF experimental setup.
In order to generate the sampling signal, a 10 GHz active ML laser source was exploited,
producing sub-ps pulses at a tunable wavelength λ
C
. The pulse train repetition rate was then
reduced down to 500 MHz by a Mach Zehnder (MZ) intensity modulator. The choice of the
sampling rate depends on many factors: the upper value is limited by the bandwidths of the
receiver and the electrical oscilloscope used for the acquisition of all the samples. On the
other hand, low sampling rates, increase the acquisition time needed to obtain a fixed
number of samples, and then require a higher memory capacity in the acquisition board. A
sampling rate equal to 500 MHz represented the best trade off, using a 1 GHz receiver and
an acquisition board with a memory capacity of 10 MPoints at a rate of 10 GSample/s. The
sampling pulses were coupled with the signal under test in a 250 m long span of HNLF
(with

γ
= 10W
-1
Km
-1
) generating the FWM components. An optical tunable filter was then
used to extract the FWM components spectrally closer to λ
C
thus obtaining a sample power
linearly dependent on the instantaneous power of the signal under test. The optical samples
were then detected through a 1 GHz bandwidth photo-receiver and measured on a 3 GHz
bandwidth oscilloscope working at 10 Gsample/s. The oscilloscope used for the experiment
was able to directly acquire and process the data exploiting MatLab scripts. The
implemented sampler has the capability to analyze a signal for very long time intervals with
high resolution and low refresh time. Considering the measure of a 10 ns long time interval
with a desired resolution of 1 ps, the corresponding refresh frequency is about 1 Hz. The
accuracy of the sampling technique, depends on the stability of the frequencies f
S
and f
C

whose mean values have to be measured and used as parameters in the data post
processing. As described before, the phase noise was considered in the range
Advances in Lasers and Electro Optics

306
10 KHz÷1 MHz. The lower limit was due to the acquisition time (lower than 10 ms) and
assuming that the mean frequency values, which are measured at each acquisition, are not
affected by noise components lower than 10 KHz. On the other hand the phase noise
components higher than 1 MHz present negligible amplitude and then can be neglected. The

resolution of the ASOF is determined by the difference T
S
- T
C
, by the maximum number of
acquired samples, and by the length of the analyzed time interval. According to eq. 5.1, the
possibility to finely change the period of the sampling signal allows to significantly modify
the sampling resolution. For this purpose, The ML source was provided with a variable
optical delay line into the cavity, in order to vary the length of the fibre ring, thus finely
changing the repetition rate of the generated sampling pulse train in the range
500 MHz÷1.5 MHz. The previous analytical investigation about the sampler phase noise was
validated sampling a Continuous Wave (CW) signal modulated with an electrical 39.9 GHz
sine. The sideband phase noise of the electrical spectrum of the clock is reported in
Fig. 14 (left) and compared with the curve related to the sampling signal in the range of
interest. The corresponding clock timing jitter, measured according to eq. 5.5, was 70 fs,
considerably higher than the 5 fs timing jitter of the ML source used as sampling signal. This
comparison justifies the assumption of neglecting the phase noise of the sampling signal in
the analytical investigation. In Fig. 16 the curve of the optical sinusoidal waveform as
measured through the analytical tool and as visualized by the implemented sampler.
In both analytical and experimental cases, the acquisition time was 1 ms and the resolution
of 50 fs. The timing jitter, directly measured in the time domain, as described before, was
156 fs and 188 fs in the analytical and experimental cases respectively. In the analytical case,
the sampling signal was an ideal delta function train and the amplitude noise, due to the
FWM generation, was not considered. Consequently, the comparison in terms of timing
jitter of the resolved curve, shows a good agreement between analysis and experiment,
confirming the accuracy of the proposed analytical investigation. The potentialities of the
ASOF, has been investigated considering a 40 Gbit/s optical NRZ signal. In this case, the
optical CW was modulated through the Mach Zehnder modulator driven by a 40 Gbit/s
data sequence supplied by a pattern generator.

Fig. 16. 40 GHz optical sinusoidal waveform analytically and experimentally sampled.
The electrical clock, as in the previous case, was the 39.9 GHz sinusoidal waveform, whose
sideband noise is reported in Fig. 14 (left). In this experiment, the acquisition time was 2 ms.
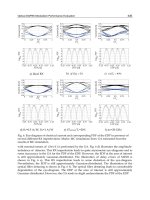
Fig. 17 shows a 32 bit-long sequence (top) and its relative eye-diagram (center), of a signal as
visualized by the proposed scheme (right) and by a commercial oscilloscope with a
Evolution of Optical Sampling

307
bandwidth of 53 GHz (left). The same comparison is reported also for the eye-diagram
modulating the signal with a (2
31
- 1)-long Pseudo Random Bit Sequence (PRBS) (bottom). In
the case of the 32 bit sequence, the time interval to be resolved was 800 ps and consequently
the mean resolution of the ASOF, was 0.8 ps. The comparison demonstrates the higher
resolution obtained with the ASOF, that can better resolve the isolated ones and zeroes. The
slight increase of the amplitude noise on the mark level in the ASOF traces, was mainly due
to the FWM term generation and amplification. For both the 32 bit sequence and the PRBS,
the higher resolution of the ASOF, allowed to obtain a good eye opening, especially close to
bit transitions. The suitability of the ASOF, to measure ultra fast signals in the whole C-
band, has been also demonstrated. Depending on the signal wavelength, the sampling pulse
train wavelength can be moved in different spectral regions, in order to optimize the FWM
generation.

Fig. 17. 40 Gbit/s NRZ signal, visualized by a 53 GHz commercial oscilloscope (left) and by
the ASOF (right); Bottom: eye-diagram of a (2
31
- 1)-long PRBS. The wavelength of the signal
under test was 1561 nm, while λ
C

= 1552.5 nm.
The tunability of the pulse train source has been obtained inserting into the ML cavity, a
tunable optical filter. The main specifications of the laser, such as the pulsewidth and the
time jitter, were independent on the selected wavelength in the whole C-band. Fig. 18 (left)
shows the optical spectrum at the output of the HNLF for three different wavelengths of the
40 Gbit/s signal under test: 1544 nm, 1556 nm, and 1561 nm. In all cases, the pulse train
wavelength was fixed at 1553 nm, corresponding to 9 nm, 3 nm, and 8 nm signal detuning
respectively. The same 32 bit-long sequence in the three different cases is reported in
Advances in Lasers and Electro Optics

308
Fig. 18 (right). It can be noticed that the quality of the resolved curves is comparable,
making the proposed scheme suitable for applications in the whole C-band. Moreover, the
detuning between the signal under test and the sampling pulse train was not a big issue for
the FWM generation, for signal spacing up to 9 nm. This value allows to process also ultra
fast signals with many frequency components.
As last measure, the high resolution of the ASOF, was demonstrated characterizing the
optical pulse generated by a second 10 GHz ML source at 1561 nm. In Fig. 19, the generated
optical pulse resolved by the ASOF, is reported. In this case, the timing jitter of the input
signal in the range 10 KHz÷1 MHz, was 10 fs. The acquisition time was 800 ns, and the time
span was 100 ps; consequently, the mean resolution was equal to about 0.25 ps. The
measured 3 dB pulsewidth was 4.2 ps, very close to the value of 4 ps given by a commercial
autocorrelator. The accuracy in the sampling of this short pulse, confirmed the high
performance of the proposed ASOF measuring signals with bandwidth up to 1 THz.


Fig. 18. Optical spectrum at the output of the HNLF (left) and corresponding 32 bit-long
sequence resolved by the ASOF (right) in the case of signal wavelength equal to 1544 nm
(top), 1556 nm (center), and 1561 nm (bottom).
Evolution of Optical Sampling

309

Fig. 19. trace of a 4 ps optical pulse generated by a 10 GHz ML laser source, as resolved by
the ASOF.
6. Quasi-Synchronous optical sampler
As shown in the previous sections, synchronous sampling methods can typically reach sub-
picosecond resolution, but they are able to analyze limited time intervals allowing to resolve
only the eye-diagram of a data signal. Asynchronous optical sampling methods can describe
long time intervals (> 1 ms), but with longer refresh time due to data post-processing.
Moreover they introduce a higher jitter, intrinsic in the asynchronous operation. A
possibility to obtain the advantages of both synchronous and asynchronous solutions is to
exploit quasi-synchronous sampling (QS). In particular, the implemented sampler was
based on the effect of Four Wave Mixing in high non linear fiber. It exploits the nonlinear
interaction between the signal to be resolved and a sampling ultra-short pulse train whose
frequencies are locked to a fixed difference. With this solution long bit sequences and eye-
diagram for a 640 Gb/s data-frame can be displayed without the need of data post-
processing and consequently with a very low refresh time (< 1.6 ms), exploiting low-
bandwidth electronics. A double PLL scheme able to maintain a fixed frequency mismatch is
described. Finally, sub-ps-resolution has been demonstrated by comparisons with a
commercial autocorrelator.
The working principle and the setup of the QS optical sampling oscilloscope are shown in
Fig. 20 (a,b). The sampling signal is an ultra-short pulse train at low repetition rate; when a
frequency mismatch is imposed between the repetition rates of the signal under test and the
sampling signal, a shift of the sampling signal on the signal under test is induced, as shown
in Fig. 20(a). If the signal under test is periodic with T=NT
s
(being T
s
the bit time) and N the

sequence bit number, the period of the sampling signal can be chosen as T
C
= NT
s
+ Δt,
where Δt is the desired temporal resolution. This way samples are collected consecutively,
and no post processing is required. Due to the low repetition rate, it is possible to
reconstruct the sampled signal using a slow PhotoDiode and a low-bandwidth oscilloscope,
acquiring just the samples sequence envelope. A piezoelectric delay line inside the optical
sampling source cavity makes the source acting as an Optical VCO (OVCO), allowing to
finely tune the sampling frequency f
C
. Through a double PLL scheme, the difference