CÁC BÀI THỰC HÀNH MÔN HỌC TÍN HIỆU VÀ HỆ THỐNG - Bài 2 pot

2
-
1

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
KHOA ĐIỆN














CÁC BÀI THỰC HÀNH
MÔN HỌC
TÍN HIỆU VÀ HỆ THỐNG
( 6 bài)



Họ và tên sinh viên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mã lớp thí nghiệm: . . . . . . . . . . Mã số sinh viên: . . . . . . . . . .

(Sinh viên phải nộp lại vào buổi bảo vệ tuần cuối cùng để chấm điểm)

















HÀ NỘI - 2010

2
-
2
BÀI 2
Khảo sát đáp ứng của hệ thống trên miền thời gian

I. Mục đích
 Làm quen với thư viện Simulink của MATLAB
 Sử dụng Simulink để xây dựng sơ đồ khối hệ thống và mô phỏng các tín hiệu trong hệ thống
 Sử dụng MATLAB để soạn thảo các chương trình tính tích chập, tính đáp ứng của hệ thống

trên miền thời gian
II. Yêu cầu đối với sinh viên
 Thực hiện trước bài 2.1 ở nhà.
 Đọc tài liệu hướng dẫn và trả lời được các câu hỏi của CBHD trước khi làm thực hành
 Hoàn thành nội dung bài thực hành (kể cả các bài về nhà) trước khi tham dự buổi tiếp theo
III. Nội dung
3.1 Làm quen với Simulink
Mục này do CBHD hướng dẫn cho SV (khoảng 10ph).
3.2 Vẽ đồ thị đáp ứng của hệ thống với MATLAB-Simulink
Bài 2.1 (tự chuẩn bị và làm ở nhà): Giải phương trình vi phân tuyến tính cấp hai
Cho mạch điện trên Hình 2.1, với các sơ kiện là
(0 ) 0
L
i


và
(0 ) 0.5V,
C
v

 điện áp nguồn là tín
hiệu bước nhảy đơn vị
( ).
u t
Hãy tính điện áp của tụ
điện
( ).
C
v t

Trong bài này,
C
L C
dv
i i i C
dt
   (2.1)
Và theo định luật điện áp của Kirchoff,
( ) ( ) ( )
L
L C
di
Ri t L v t u t
dt
   (2.2)
Thay (2.1) vào (2.2) ta được
2
2
( ) ( )
C C
C
dv d v
RC LC v t u t
dt dt
   (2.3)
Thay giá trị của các linh kiện vào và sắp xếp lại (2.3), ta có
2
2
1 4

( ) ( )
3 3
C C
C
d v dv
v t u t
dt dt
  
.
hay

2
2
4 3 3, 0.
C C
C
d v dv
v t
dt dt
   
(2.4)
 Các em hãy giải phương trình vi phân (2.4) và ghi lời giải vào phần dưới đây.

Hình 2.1 Mạch điện cho Bài 2.1

2
-
3



 Với kết quả tìm được ở trên, các em hãy sử dụng MATLAB để vẽ đồ thị của
( )
C
v t
vào Hình 2.2
dưới đây
0 1 2 3 4 5 6 7 8 9 10
0.5
0.6
0.7
0.8
0.9
1

Hình 2.2 Đồ thị cho lời giải của phương trình (2.4)

Bài 2.2 (thực hiện có hướng dẫn tại PTN): Mô tả hệ thống bằng mô hình trạng thái
Với mạch điện ở Bài 2.1, ta có:
0

( ) ( ) ( )
L
L C
di
Ri t L v t u t
dt
  
Nếu định nghĩa các biến trạng thái là
1
,
L
x i

2
C
x v

và tín hiệu ra là
2
C
y x v
 
đồng thời thay các
giá trị vào, ta sẽ thu được mô hình trạng thái như sau (sinh viên tự kiểm tra):

 
1 1
0
2 2
1

2
4 4 4
( )
3 4 0 0
0 1
x x
u t
x x
x
y
x
 
      
 
   
   
   
   
 

 
 


(2.5)
Sau đây chúng ta sẽ sử dụng Simulink để thu được và hiển thị tín hiệu ra
( ).
C
v t

Cách 1: Mở một file mới trong Simulink và đặt tên file là, ví dụ mhtt_2_5. Sử dụng các khối trong
Simulink Library Browser để tạo được sơ đồ khối như Hình 2.3.
Lưu ý: Khối Step nằm trong Source, khối State-Space trong Continuous, khối Bus Creator trong
Common Used Blocks, và khối Scope trong Sink.
.
Lời chú thích cho các khối có thể được
thực hiện bằng tay như sau: kích đúp
vào dưới mỗi khối và khi một hình chữ
nhật nhỏ xuất hiện cùng với con trỏ, ta
có thể gõ các thông tin cho khối đó. Để
bắt đầu một dòng mới, ta ấn phím
Enter.



Hình 2.3 Cách thu được
( )
C
v t
cho Bài 2.2 với khối State-Space

2
-
4
Tiếp theo, ta kích đúp vào khối State-Space, và trong cửa sổ Function Block Parameters, ta nhập
các thông số như Hình 2.4.

Hình 2.4 Các thông số cho khối chức năng trong khối State-Space
Các sơ kiện [x1 x2]’ được chỉ định trên Cửa sổ lệnh của MATLAB như sau
x1=0; x2=0.5;

Chúng ta cũng cần chỉ định thời gian mô phỏng. Điều này được thực hiện bằng cách, trên menu
chọn Simulation

Configuration Parameters rồi chọn thời gian mô phỏng là 10s. Để bắt đầu
mô phỏng, ta chọn Simulation

Start hoặc kích vào biểu tượng và để quan sát tín hiệu ra,
ta kích đúp vào khối Scope, rồi kích vào biểu tượng tự động co giãn đồ thị .
 Các em hãy vẽ lại đồ thị đó vào Hình 2.5 và so sánh với đồ thị ở Hình 2.2 trước đó.
0 1 2 3 4 5 6 7 8 9 10
0
0.2
0.4
0.6
0.8
1
u
0
(t)
v
C
(t)

Hình 2.5 Đồ thị của
( )
C
v t
cho Bài 2.2

Cách 2: Từ phương trình (2.4), ta có

2
2
4 3 ( )
C C
C
d v dv
v u t
dt dt
    (2.6)
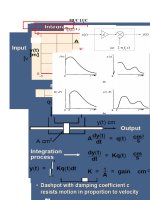
Sơ đồ khối biểu diễn quan hệ trong (2.6) được cho trên Hình 2.7.

2
-
5

Hình 2.7 Sơ đồ khối của phương trình (2.6)
 Các em hãy mở một file mới trong Simulink, đặt tên file và xây dựng sơ đồ khối tương tự như
Hình 2.7. Sau đó, hãy khai báo tham số cho các khối và thực hiện mô phỏng tín hiệu ra với thời
gian mô phỏng là 10s (CBHD kiểm tra). Vẽ lại sơ đồ Simulink đó vào khung dưới đây.
Lưu ý: Trong Simulink Library Browser, khối Add (hay Sum) và khối Gain nằm trong Math
Operations, khối Integrator nằm trong Continuous. Các sơ kiện được khai báo trong các khối
Integrator.

Bài 2.3 (thực hiện có hướng dẫn tại PTN): Tính toán và vẽ đồ thị tích chập của hai tín hiệu
Đọc chương trình MATLAB sau đây và cho biết chương trình này dùng để làm gì. Sau đó gõ
chương trình vào file soạn thảo và lưu vào với tên file conv.m.
 Các em hãy tìm hiểu và giải thích từng dòng lệnh, sau đó vẽ lại đồ thị (với chu kỳ lấy mẫu 0.01
giây) trên Hình 2.8.

% Program 2.3. Convolution of two signals

% Approximate the convolution y(t) of the signals
% x(t)=exp(-2(t-2))u(t-2) and h(t)=exp(-3(t+3))u(t+3).
% Plot the approximate convolution output.
% Plot the exact convolution output also.
% Assume that the first nonzero value of the signals start at time t=0
% and find the convolution output.
% Then, use the convolution time shift theorem to find the exact starting
% time of the convolution output.

clear; % clear variables and functions from memory

t1=2; % time of the first nonzero value of x(t)
t2=-3; % time of the first nonzero value of h(t)
t3=t1+t2; % time of the first nonzero value of convolution output

for ts=[0.2 0.1 0.01]; % sampling interval
clf; % clear current figure


2
-
6
n=0:1:4/ts; % sample index
x=exp(-2*n*ts);x(1)=0.5*x(1); % sample values of x(t)=exp(-2t)u(t)
% sample value is the average of the two limiting values at any
% discontinuity
h=exp(-3*n*ts);h(1)=0.5*h(1); % sample values of h(t)=exp(-3t)u(t)
y=ts*conv(x,h);
L=length(y);
t=ts*(0:L-1);
yf=exp(-2*t)-exp(-3*t); % exact samples of convolution
plot(t3+t,y,t3+t,yf,':') % plot with solid and dashed lines
ylabel('y(t)') % y-axis label of the graph is y(t)
xlabel('t') % x-axis label of the graph is t
legend('computed','exact')
title('convolution of e^{-2(t-2)}u(t-2) and e^{-3(t+3)}u(t+3)')
text(0.6,0.7,['sampling interval = ',num2str(ts)],'units','normalized','fontsize',10)
disp('see the graph and press any key to continue')
pause % wait until a key is pressed
end


-1 0 1 2 3 4 5 6 7
0
0.02

0.04
0.06
0.08
0.1
0.12
0.14
0.16
y(t)
t
convolution of e
-2(t-2)
u(t-2) and e
-3(t+3)
u(t+3)

Hình 2.5. Đồ thị cho Bài 2.3.

Bài 2.4 (thực hiện có hướng dẫn tại PTN): Vẽ đáp ứng của hệ thống không liên tục
Chương trình sau đây tính toán và vẽ đáp ứng của hệ thống tuyến tính không liên tục được mô tả
bởi phương trình sai phân cấp hai:













1 0.8 2 2 3 1 4 2
y n y n y n x n x n x n
        

với các sơ kiện








1 2, 2 1, 1 2 0
y y x x
        
và tín hiệu vào




0.5 .
n
x n u n

Các em hãy điền các dòng lệnh còn thiếu vào phần chấm chấm để hoàn thiện chương trình (với
gợi ý là các dòng chú thích bên cạnh) và vẽ lại đồ thị sau khi chạy mô phỏng lên Hình 2.9.

% Program 2.4. System response by iteration

% Find the response of the system, for n=0 to n=M,
% governed by second-order difference equation
% y(n)+a1 y(n-1)+a0 y(n-2)=b2 x(n)+b1 x(n-1)+b0 x(n-2)
% by iteration to the input x(n)= (0.5)^n u(n)
% with the given initial conditions, y(-1) and y(-2).
% Plot the response.

clear; % clear variables and functions from memory
clf; % clear current figure

ym1=2;ym2=-1; % initial output conditions

2
-
7
% initial input conditions
b2=2;b1=-3;b0=4; % coefficients of the input terms
% coefficients of the output terms
M=10; % iterate up to n=M
x=(0:M)*0;y=x;
for n=0:M
x(n+1)=(0.5)^n; % present input value
yc= % present output
ym2=ym1;ym1= ; % update past output values
xm2=xm1;xm1= ; % update past input values
y(n+1)=yc; % store the output values in array y
end
n=0:1:M; % discrete time base sequence

plot(n,y,'*',n,x,'o') ; % plot with '*' and 'o' symbols
grid on;
ylabel('y(n)') % y-axis label of the graph is y(n)
xlabel('n') % x-axis label of the graph is n
legend('output','input')
title('Response of a second-order system by iteration')

0 1 2 3 4 5 6 7 8 9 10
-1
0
1
2
3
4
5
y(n)
n
Response of a second-order system by iteration


output
input

Hình 2.9. Đáp ứng của hệ thống cho Bài 2.4

Bài 2.5 (về nhà tự làm)
Cho hệ thống bậc bốn được mô tả bởi mô hình trạng thái như sau:
 
0 1 0 0 0
0 0 1 0 0

0 0 0 1 0
1 0 2 0 1
1 0 0 0
x x u
y x
   
   
   
 
   
   
 
   



trong đó


1 2 3 4
T
x x x x x
 .
Các em hãy xây dựng sơ đồ khối Simulink (sử dụng khối State-space) để mô phỏng tín hiệu ra
của hệ thống ứng với sơ kiện
(0) 0,
x

tín hiệu vào
( ) sin ,

u t t

và thời gian mô phỏng là 25s. Hãy
vẽ lại tín hiệu ra đó vào Hình 2.10 dưới đây.
Lưu ý: Tín hiệu sin có thể được tạo ra từ khối Signal Generator trong Sources của Simulink
Library Browser.

2
-
8
0 5 10 15 20 25
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2

Hình 2.10. Dạng tín hiệu cho Bài 2.5


Bài 2.6 (về nhà tự làm): Tính toán và vẽ đồ thị đáp ứng của hệ thống không liên tục
Hãy sửa lại chương trình trong Bài 2.4 với các giả thiết sau đây:
ym1=1;ym2=-2; xm1=0;xm2=0; b2=3;b1=-2;b0=1;a1=0.9;a0=0.8;
x(n)=u(n).
Vẽ lại đồ thị sau khi thực hiện chương trình vào Hình 2.11.

0 1 2 3 4 5 6 7 8 9 10
-4
-3
-2
-1
0
1
2
3
y(n)
n
Response of a second-order system by iteration
output
input

Hình 2.9. Đáp ứng của hệ thống cho Bài 2.6

Bài 2.6 (về nhà tự làm) Tính toán và vẽ đồ thị đáp ứng của hệ thống liên tục
Hãy viết chương trình MATLAB để tính toán và vẽ đáp ứng
( ) ( ) ( )
y t x t h t
 
của hệ thống có đáp
ứng xung
( ) ( )
t
h t e u t

 và tín hiệu vào
( ) ( 1) ( 2).

x t u t u t
   