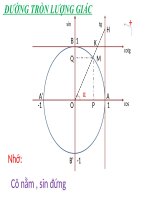
ĐƯỜNG TRÒN LƯƠNG GIÁC (hoàn chỉnh)


ĐƯNG TRN LƯNG GIC



 





















 !"
 










OP
!"#$%&'(
)*+,)#-./0123"45362$78+2+9'(
:-#;:<9)2=>?@(,*.6'(#;AB@C
D72E,!FGHIJKLFMN9)âm(,dương
#$%&
'
OP
(
OP
>
<
)
)
'
P
(
P
)
tg
α

α

OQ
OM
'
AHAH
OA
OQ

α
AH
'
OQ
=
OP
PM
OM
'
OP
'
BK
OP
OM
BK
OB
 g
α
BK
*+" !, "-&
/0 !,12"1&
/0 !,34"3&
= = =

= =
=
=
=
=
=
= =
 








 



 
















tg
α
=
PM
OP
OQ
OP


α
α
 g
α
OP
PM
OP
OQ


α
α
=
=
tg

α
= =
=
 g
α
 










OP("2+%



 
















OP
OQ
>
)
M thuc ptư I:
)
)
)
 )
α
>
)tg
α
>
)cotg
α
>
AH
BK
>
 )
α
>
>

>
)
(
π
α
< <
.5678
»
AB


 











)
M thuc ptư II:
)
)
)
 )
α

>
>
'
P
'
Q
 )
α
<
'
OP
'
OQ
<
(
π
α π
< <
'
AH
'
BK
)tg
α
<
)cotg
α
<
<
<

'
H
'
K
'
M
.5678
»
BA
′


 











>
)
M thuc ptư III:
)
)
)

)tg
α
>
)cotg
α
>
>
 )
α
<
<
(
H
(
K
(
M
(
P
(
Q
 )
α
<
(
AH
(
BK
(
OP

(
OQ
9
(
π
π α
< <
.5678
¼
A B
′ ′
<


 











.5678
)
M thuc ptư IV:
)

)
)
>
 )
α
>
<
)tg
α
<
)cotg
α
<
 )
α
<
9
H
9
K
9
Q
9
P
9
OP
9
OQ
9
AH

9
BK
9
(
(
π
α π
< <
»
B A
′
9
M
<
<
'

Q

Q

Q

R

0 1
Q

0 1
Q

OP("2+%
=
.:;<=>&
?@%- A &

Q

Q

=
R

=
'
 


OQ
2
R
 
Q
=
'
0S1
(Q28'(>0S1
Q
TU
(
(



α
α
+
(
(


α
α
=
(
'

α
(
(
'
'

tg
α
α
+ =
(Q28'(>0S1
Q
TU
(
(



α
α
(
(


α
α
(
'

α
(
(
'
'

cotg
α
α
+ =
+
=
Btg cotg
α α
=



α
α


α
α
=

   u ư ă
9 (
9
 
'

x x
tg x tg x tgx
x
+
= + + +
 a
VT
=
 

x x
x
+
(
'
 x

C' Dtgx+
(
C' Dtg x+
9 (
'tg x tg x tgx+ + +
VP
 
 
x x
x x
 
+
 ÷
 
=
=
(
C' Dtg x+
=
=
C!D
*E&!=6 :+"FG
H &
E
=
I
9 x
( I
( x x−
I J

9 (x x+ −
I I
9C  Dx x+
−
J J
(C  Dx x+
( ( ( ( ( 9 ( 9
9KC D C D L (KC D C D Lx x x x= + − +
( ( ( ( (
9KC  D (  Lx x x x= + −
( ( I I ( (
(KC  DC    DLx x x x x x− + + −
( ( (
9C' (  Dx x= −
( ( ( ( ( ( (
(B'BKC  D (    Lx x x x x x− + − −
( ( ( ( (
9 J  (C' 9  Dx x x x= − − −
( ( ( (
9 J  ( J  'x x x x= − − + =
I ( I (
 C9 ( D  C9 ( DE x x x x= − + −
=
*+5M:+"FG

)
)
)
J
π
9
π
I
π
(
π
)
9)
)
IN
)
J)
)
O)
α

α

α
tg
α
cotg
α
)

'
(
9
I
I
9
(
'
)
)
9
9
'
9
9
'
9
9
)
MV!
*E&PEGAGAGB1&
P7>Q&
9
C ( D
(
x
π
π
< <
( (

  'x x+ =
( (
 ' x x= −
(
'
'
R
 
= − −
 ÷
 
IS
IO
=
 )x >
IS IS I 9

IO R R
x = = =


x
tgx
x
=
'
R
I 9
R
−

=
' R
R
I 9
 
= −
 ÷
 
'
I 9
= −
'
cotgx
tgx
=
'
'
I 9
=
−
I 9
'
'
 
= −
 ÷
 ÷
 
I 9= −
P &

(
 x
'
'
IO
= −
D7
9
(
(
x
π
π
< <
'

R
x = −
*>!T&

WV.X""YZ[W4\./#]'(3<<,0^(:<>_
.2<4(9./#]1C

`"YWa*b*<68+.(`*]6?c
2<6?8C

UV!;W