Tính chất3 đường trung tuyến của Tam giác-Tiết 53

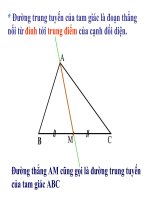
M
A
B
C
Đường thẳng AM cũng gọi là đường trung tuyến
của tam giác ABC
* Đường trung tuyến của tam giác là đoạn thẳng
nối từ đỉnh tới trung điểm của cạnh đối diện.

* Đường trung tuyến của tam giác là đoạn thẳng
nối từ đỉnh tới trung điểm của cạnh đối diện.
Cho hình vẽ:
A
B
M
C
K
1. Chọn phương án đúng trong các phương án sau:
a. CK là đường trung tuyến của tam giác ABC
b. KM là đường trung tuyến của tam giác ABC
c. AM là đường trung tuyến của tam giác ABC
2. Đoạn thẳng KM có là đường trung tuyến của tam
giác nào không? Vì sao?
Bài toán 1:

Bài toán 2:
Biết DI là đường trung tuyến của tam giác DEF.
Em hãy chọn câu trả lời đúng và đầy đủ trong các
câu sau:
a. Điểm I thuộc EF.

b. Điểm I nằm giữa hai điểm E và F.
c. Điểm I là trung điểm của cạnh EF.
?1
Hãy vẽ một tam giác với tất cả các đường
trung tuyến của nó ?

M
A
B
C
P
N
d
Mỗi tam giác có ba đường trung tuyến.

Thực hành 1:
-
Cắt một tam giác bằng giấy.
-
Gấp lại để xác định trung điểm một cạnh của nó.
-
Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện.
- Bằng cách tương tự, hãy vẽ tiếp hai đường trung
tuyến còn lại.

Thực hành 2:
-
Trên mảnh giấy kẻ ô vuông mỗi
chiều 10 ô, em hãy đếm dòng,
đánh dấu các đỉnh A, B, C rồi vẽ

tam giác ABC như hình 22.
-
Vẽ hai đường trung tuyến BE và
CF. Hai trung tuyến này cắt nhau
tại G. Tia AG cắt cạnh BC ở D.
Hình 22
.
.
.
A
B
C

Thực hành 2: Trên mảnh giấy kẻ ô
vuông mỗi chiều 10 ô, em hãy đếm
dòng, đánh dấu các đỉnh A, B, C
rồi vẽ tam giác ABC như hình 22.
Hình 22
.
.
.
A
C
B
.
A
.
B
.
C

Thực hành 2:Vẽ hai đường trung tuyến BE và CF.
Hai trung tuyến này cắt nhau tại G.
Tia AG cắt cạnh BC ở D.
.
A
.
B
.
C
.
E
.
F
.
G
D
.

.
.
.
.
.
.
A
B
C
E
F

.
G
D
Hình 22
?3
Dựa vào hình 22, hãy cho biết:
. AD có là đường trung tuyến của tam giác ABC hay không?
. Các tỉ số bằng bao nhiêu?
AG BG CG
; ;
AD BE CF

B
C
.
A
.
.
.
E
.
F
.
G
D
.
*AD là đường trung tuyến của tam giác ABC.

AG
=

AD
6
9
2
=
3
BG
=
BE
2
3
CG
=
CF
2
3
⇒ =
AG BG CG
= =
DA EB FC
2
3
GA =
Điểm G cách mỗi đỉnh một khoảng bằng độ dài
đường trung tuyến đi qua đỉnh ấy.
2
3
2 2
; GB = BE ; GC = CF
3 3

2
AD
3

nh lí:Đị
Ba đường trung tuyến của tam giác ………………………
Điểm đó cách mỗi đỉnh một khoảng bằng …. độ dài đường
trung tuyến đi qua đỉnh ấy.
G
B
C
D
E
F
A
GT ∆ABC: AD, BE, CF là ba đường
trung tuyến đồng quy tại G.
KL
AG BG CG 2
AD BE CF 3
= = =
Điểm G là trọng tâm của tam giác ABC
cùng đi qua một điểm
3
2
G

Trong tam giác ABC nếu muốn xác định trọng tâm G
ta làm như thế nào?
Cách 2:

2
3
Tìm
giao điểm
của hai
đường trung
tuyến
Vẽ một đường
trung tuyến, rồi xác
định điểm G cách đỉnh
đó bằng độ dài
đường trung tuyến ấy.
Cách 1:

Hãy điền từ hoặc cụm từ thích hợp vào chỗ trống
trong các câu sau:
3. Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng
… độ dài đường trung tuyến………………
cùng đi qua một điểm
2. Ba đường trung tuyến của tam giác……………………
điểm đó được gọi là …………………………
trọng tâm của tam giác
2
3
Bài tập 1:
1. Đường trung tuyến của tam giác là đoạn thẳng nối từ
… của tam giác tới ……………………………
đi qua đỉnh ấy.
đỉnh
trung điểm cạnh đối diện.

Bài tập 2:
D
E
H
G
F
Cho G là trọng tâm của tam giác DEF
với đường trung tuyến DH.
Trong các khẳng định sau, khẳng
định nào đúng? Khẳng định nào sai ?
.
DG 2
=
DH 3
GH 1
b. =
DH 3
a
.
GH 2
c. =
DG 3
DG
d. = 2
GH
Đ
Đ
S
Đ

* Bài 24 ( gk – 66)
a) MG = …MR
GR = …MR
b) NS = …NG
GR = …MG
NS = … GS
NG = … GS
3. Bài tập vận dụng (Hoạt động nhóm
đôi )
2
3
1
3
1
2
Cho hình 25 hãy điền số thích hợp vào
chỗ trống trong các đẳng thức sau:
3
2
3
2
E
S
R
Hình 25
G
M
P
N

Sơ đồ tư
duy

G
Có thể
em
chưa
biết
Đặt một miếng bìa hình tam giác lên giá nhọn, điểm đặt
làm cho miếng bìa đó nằm thăng bằng đó chính là trọng
tâm của tam giác.
Nếu nối 3 đỉnh của một tam giác với trọng tâm của nó thì ta
được ba tam giác nhỏ có diện tích bằng nhau.
Hãy thử xem!

-Học thuộc định lý ba đường trung tuyến của tam giác.
- Luyện vẽ trung tuyến trên giấy không kẻ ô.
- Bài tập về nhà: bài 25, 28, 29 trang 67 SGK; bài 31, 33
trang 27 SBT.
D
F
E
I
G
10cm
1
3
c
m

1
3
c
m
•
Hướng dẫn bài 28 SGK:
a) Chứng minh: ∆ DEI = ∆ DFI (xét hai tam
giác)
b)
c) Tính độ dài đường trung tuyến DI
( (tính DI theo định lí Py-ta-go
⇒DG)
DIE ; DIF là góc gì? (góc EIF là góc bẹt)

 Bài tập 25 trang 67
Biết rằng trong tam giác vuông, đường trung tuyến ứng với cạnh
huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
*Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm,
AC= 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam
giác ABC.
∆ABC vuông, theo định lí Pytago, ta có:
BC
2
= AB
2
+ AC
2
= 3
2
+ 4

2
= 25 ⇒ BC = 5 (cm)
(mà :
1
AM = BC)
2
Hướng dẫn Tính AG:
G
A
C
M
B
3cm 4cm
AM=?
BC=?