Góc có đỉnh ở bên trong, bên ngoài đường tròn

Chào mừng quý thầy cô
và các em học sinh
GV: Trần Đăng Khoa
Tổ: Tự nhiên

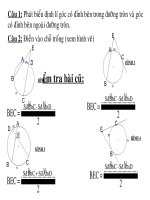
KIỂM TRA BÀI
CŨ
B =
sđ BC
2
A =
sđ BC
2
O = sđ BC
Gọi tên và nêu công thức tính số đo của các góc
được ký hiệu trong mỗi hình vẽ sau:
H1 H2
H3
Đỉnh trùng
với tâm
Đỉnh thuộc
đường tròn
Đỉnh nằm trong
đường tròn
Đỉnh nằm ngoài
đường tròn

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN

1. Góc có đỉnh ở bên trong đường tròn:
Góc AEB là góc có đỉnh ở bên trong đường tròn, chắn hai cung AB và CD.
Số đo góc AEB có
quan hệ gì với số đo
các cung AB và CD?

- Thời gian: 1 phút.
Sinh hoạt nhóm:
- Đo AEB, AB, CD.
AEB = 60
0
sđ AB = 80
0
sđ CD = 40
0
- So sánh AEB và sđ AB + sđ CD?
sđ AB + sđ CD = 80
0
+ 40
0
= 120
0
= 2.60
0
= 2.AEB
AEB =
sđ AB + sđ CD
2
Suy ra

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
1. Góc có đỉnh ở bên trong đường tròn:
Định lý: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo
hai cung bị chắn.
Góc AEB là góc có đỉnh ở bên trong đường tròn, chắn hai cung AB và CD.

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
1. Góc có đỉnh ở bên trong đường tròn:
Chứng minh
AEB =
sđ AB + sđ CD
2
AEB là góc ngoài của ∆EBD
AEB =
sđ AB
2
sđ CD
2
+
AEB =
+
EDB EBD

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN

Nhận xét quan hệ về đỉnh, cạnh của góc F với đường tròn?
Góc F có:
+ Đỉnh nằm ngoài đường tròn.
+ Hai cạnh cắt đường tròn.
Góc có đỉnh ở bên ngoài
đường tròn

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
2. Góc có đỉnh ở bên ngoài đường tròn:
m
n
Số đo góc có đỉnh bên
ngoài đường tròn có quan
hệ gì với số đo các cung bị
chắn?

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
Hình 1 Hình 2 Hình 3
2. Góc có đỉnh ở bên ngoài đường tròn:
Định lý: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số
đo hai cung bị chắn.
F =
sđ CD - sđ AB
2
m
n

F =
sđ BC – sđ AB
2
F =
sđ AmB – sđ AnB
2

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
2. Góc có đỉnh ở bên ngoài đường tròn:
F =
sđ CD - sđ AB
2
sđ CD
2
sđ AB
2
-
F =
-
F =
Chứng minh:
F =
sđ CD - sđ AB
2
CAD ADB
CAD là góc ngoài của ∆ADF
CAD = ADB
+

F

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
Hình 1 Hình 2 Hình 3
2. Góc có đỉnh ở bên ngoài đường tròn:
F =
sđ CD - sđ AB
2
F =
sđ BC – sđ AB
2
m
n
F =
sđ AmB – sđ AnB
2
x

So sánh điểm giống và khác nhau giữa góc có đỉnh ở
bên trong đường tròn và góc có đỉnh ở bên ngoài
đường tròn.

Tiết 44
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
Bài tập áp dụng:
Cho hình vẽ
Chứng minh: AD ⊥ BC.

Biết F = 50
0
, sđ AB = 40
0
. Chứng minh: AD ⊥ BC
CHD = 90
0
Tính CD
F =
sđ CD – sđ AB
2
và F = 50
0
, sđ AB = 40
0

Hướng dẫn học ở nhà:
-
Học thuộc công thức tính góc có đỉnh ở bên trong, bên
ngoài đường tròn.
-
Vẽ hình và chứng minh hai trường hợp còn lại của
định lý góc có đỉnh ở bên ngoài đường tròn.
-
Làm bài tập 36, 37, 38 trang 82 (sgk).

Bài 37/82 (sgk):
Cho đường tròn (O) và hai dây AB, AC bằng
nhau. Trên cung nhỏ AC lấy một điểm M.
Gọi S là giao điểm của AM và BC.

Chứng minh: ASC = MCA.
MCA =
sđ AM
2
ASC =
sđ AB – sđ MC
2
sđ AB – sđ MC = sđ AM
sđ AB = sđ AC
ASC = MCA
AB = AC

Xin cảm n qúy Thầy Cô ơ
và các em học sinh.