Góc có đỉnh ở bên trong và bên ngoài đường tròn

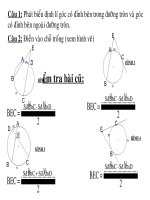
Kiểm tra bài cũ:
Câu 1: Phát biểu đònh lí góc có đỉnh bên trong đường tròn và góc
có đỉnh bên ngoài đường tròn.
Câu 2: Điền vào chỗ trống (xem hình vẽ)
·
2
...........................
BEC =
E
B
C
m
n
E
B
C
A
m
n
D
B
C
E
m
n
A
·
2
...........................
BEC =

·
2
...........................
BEC =
·
2
...........................
BEC =
E
A
B
C
m
n
D
¼
¼
SđBnC -SđAmD
¼
¼
SđBnC + SđAmD
¼
¼
SđBnC -SđAmD
¼
¼
SđBnC -SđAmD
HÌNH 1
HÌNH 2
HÌNH 3

HÌNH 4

Bài 1: Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD
lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.
Chứng minh ES = EM.
A
B
C
D
E
S
M
⊥AB CD
O
⊥EM MO
EB = EM
GT
KL
·
MSE
Chứng minh
có đỉnh S ở trong đường tròn nên:
·
»
¼
+
=
sđCA SđBM
MSE
2

·
CME
là góc tạo bởi tia tiếp tuyến và dây
cung nên:
·
¼
»
¼
+
= =
1 sđCB SđBM
CME SđCM
2 2
(1)
(2)
⊥Vì AB CD
(gt) nên

»
»
CB=CA
(3)
Từ (1),(2),(3) ta có
·
·
=MSE CME
Vậy tam giác ESM cân tại S hay ES=EM
Hình vẽ:

Bài 2: Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và

AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm trong
hình tròn. Chứng minh:
µ
A
Chứng minh
là góc có đỉnh ở ngoài đường tròn và
µ
»
¼
−
=
sđCN SđBM
A
2
·
BMS
·
»
¼
+
=
sđCN SđBM
BSM
2
(1)
(2)
(3)
Mặt khác,
·
»

=
1
CMN SđCN
2
Hình vẽ:
µ
·
·
+ =A BSM 2.CMN
chắn cung CN và cung BM nên:
là góc có đỉnh ở trong đường tròn và
chắn cung CN và cung BM nên:
Cộng (1),(2) theo từng vế, ta có:
µ
·
»
+ =A BSM SđCN
·
CMN
là góc nội tiếp nên:
(4)
Từ (1),(2),(3),(4) ta có:
µ
·
·
+ =A BSM 2.CMN

Nhóm số: . . . . . . .
Đề bài:
Xem hình vẽ, cho biết

·
»
= =
0 0
ASB 25 ;SđAB 80 .
Số đo cung CD là:
0
A.50
0
B.30
0
C.45
0
D.25
BẠN PHẢI CHỨNG MINH ĐÁP ÁN
MÀ BẠN ĐÃ CHỌN.
CHỨNG MINH