đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng

Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
VÀ ỨNG DỤNG
Trong các đề thi tuyển sinh vào Đại học và Cao đẳng thường có câu khảo sát hàm số và
các vấn đề liên quan đến đồ thị hàm số. Một nội dung thường gặp là vẽ đồ thị của hàm số có
chứa dấu giá trị tuyệt đối và ứng dụng của nó. Đây là vấn đề mà học sinh thường cảm thấy
lúng túng và khó khăn khi gặp phải.
Bài viết này cung cấp cho giáo viên một tài liệu tham khảo để hướng dẫn học sinh giải
quyết trọn vẹn và nhanh gọn khi gặp bài toán dạng này.
I. CƠ SỞ LÝ THUYẾT.
1. Các phép biến đổi đơn giản.
a. Hai điểm
( )
; M x y
và
( )
;M x y
′
−
đối xứng với nhau qua trục hoành .
b. Hai điểm
( )
; M x y
và
( )
; M x y
′
−
đối xứng với nhau qua trục tung .
c. Hai điểm

( )
; M x y
và
( )
;M x y
′
− −
đối xứng với nhau qua gốc toạ độ O .
Từ các phép biến đổi đơn giản này ta có.
2. Các phép biến đổi đồ thị.
a. Đồ thị của hai hàm số
( )
y f x=
và
( )
y f x= −
đối xứng với nhau qua trục hoành.
b. Đồ thị của hai hàm số
( )
y f x=
và
( )
y f x= −
đối xứng với nhau qua trục tung.
c. Đồ thị của hai hàm số
( )
y f x=
và
( )
y f x= − −

đối xứng với nhau qua gốc tọa độ O.
Hệ quả 1. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
Hệ quả 2. Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
Từ các kết quả trên ta có các dạng cơ bản về đồ thị của hàm số có chứa dấu giá trị tuyệt đối.
II. CÁC DẠNG CƠ BẢN.
Dạng 1. Từ đồ thị (C) của hàm số
( )
y f x=
, suy ra cách vẽ đồ thị (G) của hàm số
( )
y f x=
Lời giải. Ta có
( )
( ) ( )
( ) ( )
khi 0
khi 0
f x f x
y f x
f x f x
 ≥

= =

− <


Suy ra
( ) ( ) ( )
1 2

G C C= ∪
với
( )
1
C
là phần đồ thị (C) nằm phía trên trục hoành
( )
( )
0
C
y ≥
, còn
( )
2
C
là phần đối xứng qua trục hoành của phần đồ thị (C) nằm phía dưới trục hoành
( )
( )
0
C
y <
Ví dụ 1. Từ đồ thị (C) của hàm số
3 2
3 3y x x= − +
, vẽ đồ thị (G) của hàm số
3 2
3 3y x x= − +


Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 1

Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Dạng 2. Từ đồ thị (C) của hàm số
( )
y f x=
, suy ra cách vẽ đồ thị (H) của hàm số
( )
y f x=
Lời giải. Vì
x x− =
nên
( )
y f x=
là hàm số chẵn, suy ra đồ thị (H) nhận trục tung làm trục
đối xứng. Vì vậy
( )
( )
3 4
( )H C C= ∪
với
( )
3
C
là phần đồ thị của (C) nằm bên phải trục tung
( )
0x ≥
, còn
( )
4
C

là phần đối xứng của
( )
3
C
qua trục tung.
Ví dụ 2. Từ đồ thị (C) của hàm số
3 2
6 9 1y x x x= − + −
, vẽ đồ thị (H) của hàm số
3
2
6 9 1y x x x= − + −
.

Dạng 3. Từ đồ thị (C) của hàm số
( )
y f x=
, suy ra cách vẽ đồ thị (K) của hàm số
( )
y f x=
Lời giải. Ta có
( )
( ) ( )
( ) ( )
khi 0
khi 0
f x f x
y f x
f x f x


≥

= =

− <


Suy ra
( ) ( )
1 2
( )K H H= ∪
với
( )
1
H
là phần đồ thị của (H) của hàm số
( )
y f x=
nằm phía
trên trục hoành
( )
( )
0
H
y ≥
, còn
( )
2
H
là phần đối xứng qua trục hoành của phần đồ thị (H) ở

phía dưới trục hoành
( )
( )
0
H
y <
.
Ví dụ 3. Từ đồ thị (C) của hàm số
3 2
6 9 1y x x x= − + −
, vẽ đồ thị (K) của hàm số
3
2
6 9 1y x x x= − + −
.



Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 2
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Dạng 4. Từ đồ thị (C) của hàm số
( )
( )
u x
y
v x
=
, suy ra cách vẽ đồ thị (L) của hàm số
( )

( )
u x
y
v x
=
Lời giải.
( )
( )
( )
( )
( )
( )
( )
( )
khi 0
khi 0
u x
u x
v x
u x
y
v x
u x
u x
v x

≥


= =



− <


Suy ra
( ) ( ) ( )
1 2
L C C= ∪
với
( )
1
C
là phần của đồ thị (C) có hoành độ thỏa mãn điều kiện
( )
0u x ≥
và
( )
2
C
là phần đối xứng qua trục hoành của phần đồ thị (C) có hoành độ thỏa mãn
( )
0u x <
.
Ví dụ 4. Từ đồ thị (C) của hàm số
2 4
3
x
y
x

−
=
−
, vẽ đồ thị (L) của hàm số
2 4
3
x
y
x
−
=
−
.
Ta có
2 4
khi 2
2 4
3
2 4
3
khi 2
3
x
x
x
x
y
x
x
x

x
−

≥

−

−
= =

−
−

− <

−



Dạng 5. Từ đồ thị (C) của hàm số
( )
( )
u x
y
v x
=
, suy ra cách vẽ đồ thị (M) của hàm số
( )
( )
u x

y
v x
=
.
Lời giải.
( )
( )
( )
( )
( )
( )
( )
( )
khi 0
khi 0
u x
v x
v x
u x
y
v x
u x
v x
v x

>


= =



− <


Suy ra
( )
( )
( )
3 4
M C C= ∪
với
( )
3
C
là phần của đồ thị (C) có hoành độ thỏa mãn điều kiện
( )
0v x >
và
( )
4
C
là phần đối xứng qua trục hoành của phần đồ thị (C) có hoành độ thỏa mãn
( )
0v x <
.

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 3
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Ví dụ 5. Từ đồ thị (C) của hàm số

2 4
3
x
y
x
−
=
−
, vẽ đồ thị (M) của hàm số
2 4
3
x
y
x
−
=
−
.
Ta có
2 4
khi 3
2 4
3
2 4
3
khi 3
3
x
x
x

x
y
x
x
x
x
−

>

−

−
= =

−
−

− <

−


Dạng 6. Từ đồ thị (C) của hàm số
( )
( )
u x
y
v x
=

, suy ra cách vẽ đồ thị (N) của hàm số
( )
( )
u x
y
v x
=
.
Lời giải.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
khi 0
khi 0
u x u x
v x v x
u x
y
v x
u x u x
v x v x

≥



= =


− <


Suy ra
( )
( )
( )
5
6
N C C= ∪
với
( )
5
C
là phần của đồ thị (C) nằm phía trên trục hoành
( )
( )
0
C
y ≥

và
( )
6
C

là phần đối xứng qua trục hoành của phần đồ thị (C) nằm phía dưới trục hoành
( )
( )
0
C
y <
.
Ví dụ 6. Từ đồ thị (C) của hàm số
2 4
3
x
y
x
−
=
−
, vẽ đồ thị (N) của hàm số
2 4
3
x
y
x
−
=
−
.
Ta có
2 4 2 4
khi 0
2 4

3 3
2 4 2 4
3
khi 0
3 3
x x
x
x x
y
x x
x
x x
− −

≥

−

− −
= =

− −
−

− <

− −


Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 4

Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.


Dạng 7. Từ đồ thị (C) của hàm số
( )
( )
u x
y
v x
=
, suy ra cách vẽ đồ thị (Q) của hàm số
( )
( )
u x
y
v x
=
.
Lời giải. Vì
x x− =
nên
( )
( )
u x
y
v x
=
là hàm số chẵn, suy ra đồ thị (Q) nhận trục tung làm trục
đối xứng. Vì vậy
( )

( )
7
8
( )Q C C= ∪
với
( )
7
C
là phần đồ thị của (C) nằm bên phải trục tung
( )
0x ≥
, còn
( )
8
C
là phần đối xứng của
( )
7
C
qua trục tung.
Ví dụ 7. Từ đồ thị (C) của hàm số
2 4
3
x
y
x
−
=
−
, vẽ đồ thị (Q) của hàm số

2 4
3
x
y
x
−
=
−
.


Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 5
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Dạng 8. Từ đồ thị (C) của hàm số
( )
( )
u x
y
v x
=
, suy ra cách vẽ đồ thị (R) của hàm số
( )
( )
u x
y
v x
=
Lời giải.
( )

( )
( )
( )
( )
( )
( )
( )
( )
( )
khi 0
khi 0
u x u x
v x v x
u x
y
v x
u x u x
v x v x

≥


= =


− <


Suy ra
( )

( ) ( )
1 2
R Q Q= ∪
với
( )
1
Q
là phần đồ thị (Q) của hàm số
( )
( )
u x
y
v x
=
nằm phía trên
trục hoành
( )
( )
0
Q
y ≥
, còn
( )
2
Q
là phần đối xứng qua trục hoành của phần đồ thị (Q) ở phía
dưới trục hoành
( )
( )
0

Q
y <
.
Ví dụ 8. Từ đồ thị (C) của hàm số
2 4
3
x
y
x
−
=
−
, vẽ đồ thị (R) của hàm số
2 4
3
x
y
x
−
=
−
Ta có
( )
( )
2 4 2 4
khi 0
3 3
2 4
3
2 4 2 4

khi 0
3 3
x x
f x
x x
x
y
x
x x
f x
x x

− −
= ≥

− −
−

= =

−
− −

− = <

− −

Suy ra
( ) ( )
1 2

( )K H H= ∪
với
( )
1
H
là phần đồ thị của (H) của hàm số
( )
y f x=
nằm phía
trên trục hoành
( )
( )
0
H
y ≥
, còn
( )
2
H
là phần đối xứng qua trục hoành của phần đồ thị (H) ở
phía dưới trục hoành
( )
( )
0
H
y <
.
III. ỨNG DỤNG.
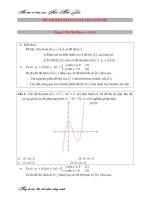
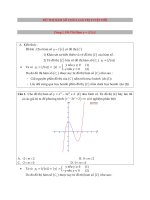
Bài tập 1. (Đề TSĐH khối A năm 2006)
1) Khảo sát sự biến thiên và vẽ đồ thị hàm số

3 2
2 9 12 4y x x x= − + −
.
2) Tìm m để phương trình sau có 6 nghiệm phân biệt
3
2
2 9 12x x x m− + =
.

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 6
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Lời giải.
1) Đồ thị (C) của hàm số
3 2
2 9 12 4y x x x= − + −
như hình vẽ

2) Áp dụng dạng 2, từ đồ thị (C) của hàm số
3 2
2 9 12 4y x x x= − + −
ta vẽ được đồ thị
( )
1
C
của hàm số
3
2
2 9 12 4y x x x= − + −
.

Từ đó suy ra phương trình
3
2
2 9 12x x x m− + =
có 6 nghiệm phân biệt khi và chỉ khi phương
trình
3
2
2 9 12 4 4x x x m− + − = −
có 6 nghiệm phân biệt
⇔
Đường thẳng
4y m= −
cắt đồ thị
( )
1
C
tại 6 điểm phân biệt
0 4 1 4 5m m⇔ < − < ⇔ < <
.
Bài tập 2. (Đề TSĐH khối B năm 2009)
Cho hàm số
4 2
2 4y x x= −
(1)
1) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1).
2) Với các giá trị nào của m, phương trình
2 2
2x x m− =
có đúng 6 nghiệm thực phân biệt ?

Lời giải.
1) Đồ thị (C) của hàm số
4 2
2 4y x x= −
như hình vẽ.


Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 7
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

2) Áp dụng dạng 1, từ đồ thị (C) của hàm số
4 2
2 4y x x= −
ta vẽ được đồ thị
( )
2
C
của
hàm số
4 2
2 4y x x= −
.
Từ đó suy ra phương trình
2 2
2x x m− =
có đúng 6 nghiệm thực phân biệt khi và chỉ khi
phương trình
4 2
2 4 2x x m− =
có đúng 6 nghiệm thực phân biệt

⇔
Đường thẳng
2y m=
cắt
đồ thị
( )
2
C
tại 6 điểm phân biệt
0 2 2 0 1m m
⇔ < < ⇔ < <
.
Bài tập 3. Cho hàm số
3
3y x x= −
.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình
( )
sin cos2 5 2t t m− =
có 4 nghiệm phân biệt
[
)
0; 2t
π
∈
.
Lời giải.
1) Đồ thị (C) của hàm số
3

3y x x= −
như hình vẽ.


2) Ta có phương trình
( )
sin cos2 5 2t t m+ =
( )
2
sin 1 2sin 5 2t t m⇔ − + =

( )
2
sin 3 sint t m⇔ − =
3
sin 3sint t m⇔ − =
(1)
Đặt
sinx t=
, vì
[
)
0; 2t
π
∈
nên
[ ]
1; 1x∈ −
và mỗi giá trị
( )

1; 1x ∈ −
cho hai giá trị
[
)
3
0; 2 \ ;
2 2
t
π π
π
 
∈
 
 
. Còn khi
1x
=
thì
2
t
π
=
; khi
1x
= −
thì
3
2
t
π

=
.
Khi đó phương trình (1) trở thành
3
3x x m− =
(2)
Phương trình (1) có bốn nghiệm phân biệt
[
)
0; 2t
π
∈
khi và chỉ khi phương trình (2) có hai
nghiệm phân biệt
( )
1; 1x ∈ −
⇔
Đường thẳng
y m=
cắt đồ thị (G) của hàm số
3
3y x x= −
tại
hai điểm phân biệt có hoành độ thuộc
( )
1; 1−
.
Áp dụng dạng 1, từ đồ thị (C) của hàm số
3
3y x x= −

ta vẽ được đồ thị (G) của hàm số
3
3y x x= −
như hình vẽ.
Dựa vào đồ thị (G) ta có đường thẳng
y m=
cắt đồ thị (G) của hàm số
3
3y x x= −
tại hai
điểm phân biệt có hoành độ thuộc
( )
1; 1−
khi và chỉ khi
0 2m
< <
.

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 8
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Bài tập 4. Cho hàm số
4 2
2 2y x x= − −
.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm m để phương trình
4
2
2

tan
cos
t m
t
− =
có 6 nghiệm phân biệt
;
2 2
t
π π
 
∈ −
 ÷
 
.
Lời giải.
1) Đồ thị (C) của hàm số
4 2
2 2y x x= − −
như hình vẽ.


2) Ta có phương trình
4
2
2
tan
cos
t m
t

− =
4 2
tan 2tan 2t t m⇔ − − =
(1)
Đặt
tanx t=
, vì
;
2 2
t
π π
 
∈ −
 ÷
 
nên
x ∈¡
. Hàm số
tanx t=
là đồng biến trên khoảng
;
2 2
π π
 
−
 ÷
 
nên mỗi giá trị x cho tương ứng một giá trị t.
Khi đó phương trình (1) trở thành
4 2

2 2x x m⇔ − − =
(2)
Suy ra phương trình (1) có 6 nghiệm t phân biệt thuộc
;
2 2
π π
 
−
 ÷
 
khi và chỉ khi phương trình
(2) có 6 nghiệm x phân biệt thuộc
¡
⇔
Đường thẳng
y m=
cắt đồ thị
2
( )C
của hàm số
4 2
2 2y x x= − −
tại 6 điểm phân biệt.
Áp dụng dạng 1, từ đồ thị (C) của hàm số
4 2
2 2y x x= − −
, suy ra đồ thị
2
( )C
của hàm số

4 2
2 2y x x= − −
như hình vẽ.
Dựa vào đồ thị
2
( )C
, suy ra đường thẳng
y m=
cắt đồ thị
2
( )C
của hàm số
4 2
2 2y x x= − −

tại 6 điểm phân biệt khi và chỉ khi
2 3m
< <
.
Bài tập 5. Cho hàm số
2
1
x
y
x
=
−
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2) Biện luận theo tham số m số nghiệm
[ ]

1; 2x ∈ −
của phương trình sau
( )
2 0m x m− − =

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 9
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

3) Tìm m để phương trình sau có 4 nghiệm t phân biệt :
( )
1
2 0m t m
t
− + − =
.
Lời giải.
1) Đồ thị (C) của hàm số
2
1
x
y
x
=
−
như hình vẽ


2) Ta có phương trình
( )
2 0m x m− − =

( )
1 2m x x⇔ − =
(1)
Ta có
1x
≠ ±
, vì nếu
1x
= ±
thì phương trình (1) trở thành
0 2
=
(vô lý).
Khi đó phương trình (1)
2
1
x
m
x
⇔ =
−
, với
( ) (
]
1; 1 1; 2x ∈ − ∪
.
Số nghiệm
[ ]
1; 2x ∈ −
của phương trình (1) bằng số giao điểm của đồ thị

( )
3
C
của hàm số
2
1
x
y
x
=
−
và đường thẳng
y m=
trên khoảng
( )
1; 1−
hoặc nửa khoảng
(
]
1; 2
.
Áp dụng dạng 2, từ đồ thị (C) của hàm số
2
1
x
y
x
=
−
suy ra đồ thị

( )
3
C
của hàm số
2
1
x
y
x
=
−

như hình vẽ. Dựa vào đồ thị
( )
3
C
ta có:
+
0m
<
: phương trình (1) có 2 nghiệm
( )
1; 1x ∈ −
.
+
0m =
: phương trình (1) có 1 nghiệm
0x =
.
+

0 4m
< <
: phương trình (1) vô nghiệm .
+
4m =
: phương trình (1) có 1 nghiệm
2x =
.
+
4m >
: phương trình (1) có 1 nghiệm
( )
1; 2x∈
.
3) Điều kiện
0t ≠
. Ta có
( )
1
2 0m t m
t
− + − =

1 1
1 2m t t
t t
 
⇔ + − = +
 ÷
 

(2)
Đặt
1
x t
t
= +
1 1
2x t t
t t
⇒ = + = + ≥
(khi
2 1x t= ⇔ =
hoặc
2 1x t= − ⇔ = −
)

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 10
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Khi đó phương trình (2) trở thành
( )
1 2m x x− =

2
1
x
m
x
⇔ =
−

(3)
Chú ý rằng
1
x t
t
= +

2
1 0t xt⇔ − + =
(
)
2
1
4
2
t x x⇔ = ± −
nên mỗi giá trị
( ) ( )
; 2 2;x ∈ −∞ − ∪ +∞
tương ứng với hai
giá trị
{ }
\ 0t ∈¡
. Suy ra:
Phương trình (2) có 4 nghiệm phân biệt
0t
≠
khi và chỉ khi phương trình (3) có
2 nghiệm
( ) ( )

; 2 2;x ∈ −∞ − ∪ +∞
⇔
Đồ thị
( )
3
C
của hàm số
2
1
x
y
x
=
−

cắt đường thẳng
y m=
tại 2 điểm phân
biệt có hoành độ
( ) ( )
; 2 2;x ∈ −∞ − ∪ +∞
2 4m
⇔ < <
.
Bài tập 6. Cho hàm số
2 1
1
x
y
x

+
=
−
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2) Tìm m để phương trình
2 2
log 1 2log 1 0t m t− − − =
có hai nghiệm t phân biệt.
Lời giải.
1) Đồ thị (C) của hàm số
2 1
1
x
y
x
+
=
−
như hình vẽ


2) Điều kiện
0t
>
. Đặt
2
logx t=
thì
x
t e=

, suy ra mỗi giá trị
x
∈
¡
tương ứng với một
giá trị
0t
>
. Khi đó phương trình đã cho trở thành
1 2 1 0x m x− − − =
(1)
Nếu
1x =
thì phương trình (1)
1 0⇔ − =
(vô lý).

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 11
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Do đó
1x
≠
. Khi đó (1)
2 1
1
x
m
x
+

⇔ =
−
(2)
Áp dụng dạng 5, từ đồ thị (C) của hàm số
2 1
1
x
y
x
+
=
−
suy ra đồ thị
( )
4
C
của hàm số
2 1
1
x
y
x
+
=
−

như hình vẽ. Dựa vào đồ thị
( )
4
C

ta có
Phương trình đã cho có hai nghiệm phân biệt
0t >
khi và chỉ khi phương trình (2) có hai
nghiệm
x ∈¡
⇔
Đồ thị
( )
4
C
của hàm số
2 1
1
x
y
x
+
=
−
cắt đường thẳng
y m=
tại hai điểm phân
biệt
2m
⇔ >
.
Bài tập 7. Cho hàm số
1
2

x
y
x
−
=
−
.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2) Tìm m để phương trình
2
sin 2 2sin 2 sin 2 2 0
4
t t m t m
π
 
− + + − =
 ÷
 
có hai nghiệm t
phân biệt thuộc đoạn
3
;
8 8
π π
 
−
 
 
.
Lời giải.

1) Đồ thị (C) của hàm số
1
2
x
y
x
−
=
−
như hình vẽ
2) Ta có phương trình
2
sin 2 2sin 2 sin 2 2 0
4
t t m t m
π
 
− + + − =
 ÷
 

( )
sin 2 1 cos2 2 sin 2 2 0
4
t x m t m
π
 
⇔ − − + + − =
 ÷
 

sin 2 cos2 1 2 sin 2 2 0
4
t x m t m
π
 
⇔ + − + + − =
 ÷
 

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 12
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

2 sin 2 1 2 sin 2 2 0
4 4
t m t m
π π
   
⇔ + − + + − =
 ÷  ÷
   
(1)
Đặt
2 sin 2
4
x t
π
 
= +
 ÷
 

. Vì
3
8 8
t
π π
− ≤ ≤
3
2
4 4
t
π π
⇔ − ≤ ≤
2
2 4 2
t
π π π
⇔ − ≤ + ≤
Suy ra
1 sin 2 1
4
t
π
 
− ≤ + ≤
 ÷
 
2 2 sin 2 2
4
t
π

 
⇔ − ≤ + ≤
 ÷
 
2 2x⇒ − ≤ ≤
.
Do đó mỗi giá trị
2; 2x
 
∈ −
 
tương
ứng với một giá trị
3
;
8 8
t
π π
 
∈ −
 
 
.
Khi đó phương trình (1) trở thành

1 2 0x mx m− + − =

( )
1 2x m x⇔ − = −
(2)

Nếu
2x =
thì (2)
1 0⇔ =
(vô lý).
Vậy
2x ≠
, do đó (2)
1
2
x
m
x
−
⇔ =
−
(3)
Áp dụng dạng 4, từ đồ thị (C) của hàm số
1
2
x
y
x
−
=
−
, suy ra đồ thị
( )
5
C

của hàm số
1
2
x
y
x
−
=
−

như hình vẽ. Từ đồ thị
( )
5
C
suy ra:
Phương trình đã cho có hai nghiệm phân biệt
3
;
8 8
t
π π
 
∈ −
 
 
khi và chỉ khi phương trình (3) có
hai nghiệm phân biệt
2; 2x
 
∈ −

 
⇔
Đồ thị
( )
5
C
của hàm số
1
2
x
y
x
−
=
−
cắt đường thẳng
y m=
tại hai điểm phân biệt có hoành độ thuộc đoạn
2; 2
 
−
 
2
0
2
m⇔ < ≤
.
Bài tập 8. Cho hàm số
3 3
2

x
y
x
−
=
−
.
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2) Tìm m để phương trình
2 2
3 9 1 9 2 0t m t− − − − − =
có 4 nghiệm t phân biệt.
Lời giải.
1) Đồ thị (C) của hàm số
3 3
2
x
y
x
−
=
−
như hình vẽ.
2) Ta có phương trình
2 2
3 9 1 9 2 0t m t− − − − − =
(1)
Điều kiện
3 3t− ≤ ≤
. Đặt

2
9x t= −
thì
2
0 9 3x t≤ = − ≤
suy ra
2
9t x= ± −
.
Do đó với mỗi giá trị
[ ]
0; 3x∈
tương ứng với hai giá trị
[ ]
3; 3t ∈ −
.

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 13
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

Khi đó phương trình (1) trở thành
3 1 2 0x m x− − − =
(2)
Nếu
2x =
thì phương trình (2)
3 0⇔ =
(vô lý) nên
2x ≠
. Do đó (2)

3 3
2
x
m
x
−
⇔ =
−
(3)
Phương trình (1) có 4 nghiệm t phân biệt thuộc
[ ]
3; 3−
khi và chỉ khi phương trình (2) có 2
nghiệm x phân biệt thuộc
[ ]
0; 3
⇔
Đường thẳng
y m=
cắt đồ thị
( )
6
C
của hàm số
3 3
2
x
y
x
−

=
−
tại 2 điểm phân biệt có hoành độ thuộc
[
) (
]
0; 2 2; 3∪
.
Áp dụng dạng 6, từ đồ thị (C) của hàm số
3 3
2
x
y
x
−
=
−
suy ra đồ thị
( )
6
C
của hàm số
3 3
2
x
y
x
−
=
−

như hình vẽ.
Từ đồ thị
( )
6
C
suy ra đường thẳng
y m=
cắt đồ thị
( )
6
C
của hàm số
3 3
2
x
y
x
−
=
−
tại 2 điểm
phân biệt có hoành độ thuộc
[
) (
]
0; 2 2; 3∪
khi và chỉ khi
3
0
2

m< ≤
hoặc
6m ≥
.
Bài tập 9. Cho hàm số
2
1
x
y
x
=
−
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
2) Tìm m để phương trình sau có hai nghiệm phân biệt
;
2 2
t
π π
 
∈ −
 ÷
 
:
( )
2
cos sin 1 0t m t m+ − + =
.
Lời giải.
1) Đồ thị (C) của hàm số
2

1
x
y
x
=
−
như hình vẽ.
2) Phương trình đã cho tương đương với
( )
2
1 sin sin 1 0t m t m− + − + =

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 14
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.


( )
2
sin 1 sinm t t⇔ − =
(1)
Đặt
sinx t=
,
;
2 2
t
π π
 
∈ −
 ÷

 
( )
1; 1x⇒ ∈ −
.
Khi đó (1) trở thành
( )
2
1m x x− =
2
1
x
m
x
⇔ =
−
(2), với mọi
( )
1; 1x ∈ −
.
Áp dụng dạng 7, từ đồ thị (C) của hàm số
2
1
x
y
x
=
−
, suy ra đồ thị
( )
7

C
của hàm số
2
1
x
y
x
=
−

như hình vẽ. Từ đó suy ra:
Phương trình (1) có hai nghiệm phân biệt
;
2 2
t
π π
 
∈ −
 ÷
 
khi và chỉ khi phương trình (2) có hai
nghiệm phân biệt
( )
1; 1x ∈ −
⇔
Đồ thị
( )
7
C
của hàm số

2
1
x
y
x
=
−
cắt đường thẳng
y m=
tại
hai điểm phân biệt có hoành độ thuộc khoảng
( )
1; 1−
0m⇔ <
.



Trên đây là một số dạng thường gặp về đồ thị của hàm số chứa dấu giá trị tuyệt đối và
một số bài toán ứng dụng của nó. Mong rằng bài viết này góp phần cung cấp tài liệu cho giáo
viên để giảng dạy học sinh ôn thi vào đại học và cao đẳng có hiệu quả.
Cuối cùng, kính chúc quý thầy cô sức khỏe, hạnh phúc và thành đạt.


Nguyễn Văn Thiết

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 15
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.

MỤC LỤC

Lời mở đầu ……………………………………… trang 1
I. CƠ SỞ LÝ THUYẾT ……………………………………………… 1
1. Các phép biến đổi đơn giản
2. Các phép biến đổi đồ thị
Hệ quả 1
Hệ quả 2
II. CÁC DẠNG CƠ BẢN …………………………………………… 1
Dạng 1. Đồ thị hàm số
( )
y f x=
. ……………………………… 1
Dạng 2. Đồ thị hàm số
( )
y f x=
…………………………………2
Dạng 3. Đồ thị hàm số
( )
y f x=
……………………………… 2
Dạng 4. Đồ thị hàm số
( )
( )
u x
y
v x
=
……………………………… 3
Dạng 5. Đồ thị hàm số
( )

( )
u x
y
v x
=
……………………………… 3
Dạng 6. Đồ thị hàm số
( )
( )
u x
y
v x
=
……………………………… 4
Dạng 7. Đồ thị hàm số
( )
( )
u x
y
v x
=
……………………………… 5
Dạng 8. Đồ thị hàm số
( )
( )
u x
y
v x
=
……………………………… 6

III. ỨNG DỤNG …………………………………………………… 6
Bài tập 1. …………………………………………………… 6
Bài tập 2. …………………………………………………… 7
Bài tập 3. …………………………………………………… 8
Bài tập 4. …………………………………………………… 9
Bài tập 5. …………………………………………………… 9
Bài tập 6. ………………………………………………… 11
Bài tập 7. ………………………………………………… 12
Bài tập 8. ………………………………………………… 13
Bài tập 9. ………………………………………………… 14
Kết luận ………………………………………………… 15
Mục lục ………………………………………………… 16

Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 16
Đồ thị hàm số chứa dấu giá trị tuyệt đối và ứng dụng.



Thầy giáo Nguyễn Văn Thiết, trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 17