Đường trung bình của hình thang (bgdt T8)

Bài giảng
TRƯỜNG THCS NGUYỄN HUỆ THÀNH PHỐ QUY NHƠN
Năm học 2008 - 2009

Kiểm tra kiến thức cũ
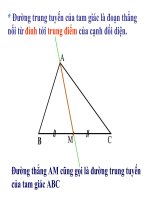
Đònh nghóa : Đường trung bình của tam giác là đoạn
thẳng nối trung điểm hai cạnh của tam giác.
Tính chất : Đường trung bình của tam giác thì song
song với cạnh thứ ba và bằng nửa cạnh ấy.
2) Cho hình thang ABCD (AB // CD) nh hìnhư v . ẽ
Tính x, y.
1) Phát biểu đònh nghóa, tính chất về đường trung bình của
tam giác.
2 cm 1 cm
M
y
E
x
F
D
C
B
A
1
EM DC
2
⇒ =
∆ ACB có MF là đường trung bình
∆ ACD có EM là đường trung bình
1

MF AB
2
⇒ =
⇒ y = DC = 2EM = 2.2 = 4 (cm)
⇒ x = AB = 2MF = 2.1 = 2 (cm)

D
C
BA
2. Đường trung bình của hình thang
4?
Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường
thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F.
Có nhận xét gì về vò trí của điểm I trên AC, điểm F trên BC ?
E
I
F
Nhận xét : I là trung điểm của AC, F là trung
điểm của BC
Đònh lí 3 : Đường thẳng đi qua trung điểm một cạnh bên của hình thang
và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
GT
KL
ABCD là hình thang (AB // CD)
AE = ED, EF // AB, EF // CD
BF = FC
∆ADC có :
ED = EA (gt)
EI // CD (gt)
⇒ I là trung điểm của AC

∆ABC có :
IA = IC (c/m trên)
IF // AB (gt)
⇒ F là trung điểm của BC
Chứng minh : Gọi I là giao điểm của AC và EF

Đònh nghóa : Đường trung bình của hình thang
là đoạn thẳng nối trung điểm hai cạnh bên của
hÌnh thang.
FE
D C
BA
Tiết 6
§4. ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC,
CỦA HÌNH THANG (tt)

Đònh lí 4. Đường trung bình của hình thang thì song song với hai đáy và
bằng nửa tổng hai đáy.
A
B
C
D
F
E
K
1
2
1
GT
KL

Hình thang ABCD (AB // CD)
AE = ED ; BF = FC
EF // AB ; EF // CD
AB+CD
EF =
2
Gợi ý chứng minh :
Tạo ra một tam giác có EF là đường trung bình và cạnh thứ ba
chứa một trong hai cạnh AB hoặc CD và có tổng là AB + CD.
Kéo dài AF cắt đường thẳng CD tại K.
Chứng minh EF là đường trung bình của tam giác ADK
Cần có : FA = FK
⇑
∆FBA = ∆FCK
⇐
FA = FB (gt)
$ $
1 2
F F=
(đối đỉnh)
µ µ
1
B C=
(so le trong do AB // DK)
Từ đó chứng minh được đònh lí
Chứng minh :
Xét , chúng có :
⇒
∆FBA = ∆FCK (g.c.g)
⇒

FA = FK và AB = CK (hai cạnh tương ứng)

A
B
C
D
F
E
K
1
2
1
∆ADK có :
E là trung điểm của AD,
F là trung điểm của AK.
⇒
⇒ EF là đường trung bình của ∆ADK
1
EF = DK
2
⇒
EF // DK (tức là EF // CD và EF // AB
Mặt khác KK = DC + CK = DC + AB, do đó :
DC+AB
EF =
2
Đònh lí trên có thể chứng minh cách khác(dựa vào bài kiểm tra đầu giờ) :
A
B
D C

E
F
M
Nối AC gọi M là trung điểm của AC
∆ACD có EM là đường trung bình
⇒ EM // DC và EM =
DC
2
∆ACB có MF là đường trung bình
⇒ MF // AB và MF =
AB
2
Qua M có ME // DC (c/m trên)
MF // AB (c/m trên)
mà AB // DC (gt)
⇒
E, M, F thẳng hàng (Tiên đề Ơclit)