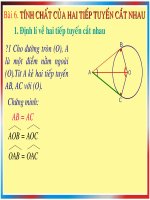Tính chất hai tiếp tuyên cắt nhau

A
B
C
O
Gi¸o viªn so¹n : Vò ThÞ Minh HuÖ
Gi¸o viªn d¹y : Vò ThÞ Minh HuÖ
Tr­êng THCS Xu©n Khª


A B
C
D
Th­íc ch÷ T
Th­íc ch÷ T
Th­íc ph©n gi¸c
Th­íc ph©n gi¸c






1.§Þnh lý vÒ hai tiÕp tuyÕn c¾t nhau
1.§Þnh lý vÒ hai tiÕp tuyÕn c¾t nhau
A
B
C
O
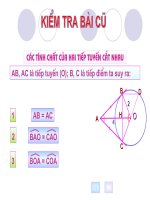
NÕu hai tiÕp tuyÕn AB vµ AC cña ®­êng trßn t©m O

c¾t nhau t¹i ®iÓm A th× :
+ §iÓm A c¸ch ®Òu hai tiÕp ®iÓm B vµ C.
+ Tia AO lµ tia ph©n gi¸c cña gãc t¹o bëi hai tiÕp
tuyÕn AB vµ AC.
+ Tia OA lµ tia ph©n gi¸c cña gãc t¹o bëi hai b¸n
kÝnh OB vµ OC .




§Þnh lý:
§Þnh lý:
NÕu hai tiÕp tuyÕn cña mét ®­êng trßn c¾t nhau t¹i mét ®iÓm th×:
NÕu hai tiÕp tuyÕn cña mét ®­êng trßn c¾t nhau t¹i mét ®iÓm th×:


+ §iÓm ®ã c¸ch ®Òu hai tiÕp ®iÓm.
+ §iÓm ®ã c¸ch ®Òu hai tiÕp ®iÓm.


+Tia kÎ tõ ®iÓm ®ã ®i qua t©m lµ tia ph©n gi¸c cña gãc t¹o bëi hai
+Tia kÎ tõ ®iÓm ®ã ®i qua t©m lµ tia ph©n gi¸c cña gãc t¹o bëi hai
tiÕp tuyÕn.
tiÕp tuyÕn.


+Tia kÎ tõ t©m ®i qua ®iÓm ®ã lµ tia ph©n gi¸c cña gãc t¹o bëi hai
+Tia kÎ tõ t©m ®i qua ®iÓm ®ã lµ tia ph©n gi¸c cña gãc t¹o bëi hai
b¸n kÝnh ®i qua c¸c tiÕp ®iÓm .
b¸n kÝnh ®i qua c¸c tiÕp ®iÓm .

A
A
B
B
C
C
O
O
O
O
’
’




Chứng minh
Chứng minh
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:


AC = CM
AC = CM


DM = DB
DM = DB

Mà CD = CM + MD
Mà CD = CM + MD






CD = AC + DB
CD = AC + DB
Cho nửa đường tròn tâm O, đường kính AB . Kẻ các tiếp tuyến Ax, By. Điểm M thuộc
Cho nửa đường tròn tâm O, đường kính AB . Kẻ các tiếp tuyến Ax, By. Điểm M thuộc
nửa đường tròn, tiếp tuyến tại M cắt Ax, By lần lượt tại C và D
nửa đường tròn, tiếp tuyến tại M cắt Ax, By lần lượt tại C và D
( hình vẽ ).
( hình vẽ ).


Chứng minh rằng : CD = AC + BD
Chứng minh rằng : CD = AC + BD
Bài tập1
Bài tập1
A
A
B
B
C
C

D
D
O
O
M
M
x
x
y
y