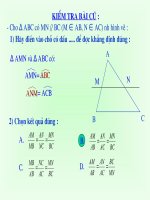khái niệm tam giác đồng dạng

PHÒNG GIÁO DỤC & ĐÀO TẠO ĐẠI LỘC
TRƯỜNG THCS NGUYỄN DU
HÂN HẠNH CHÀO ĐÓN QUÝ THẦY CÔ VÀ
CÁC EM HỌC SINH
Giáo viên thực hiện : Dương vũ Tường Vi

A
B
C
Kiểm tra:
a
M
N
ΔABC, MN// BC
(M AB, N AC )
∈
∈
AB
AM
AC
AN
BC
MN
==
GT
KL
AB
AM
AC
AN

BC
MN
==
Cho ΔABC, MN // BC
Hệ quả định lí Talet

Tiết 41: KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

Bài tập ?1: Cho tam giác ABC và A’B’C’
Ta có
Tính các tỉ số
;
''
AB
BA
;
''
BC
CB
CA
AC ''
A’ = A;
B’ = B;
C’ = C
AB
BA ''
BC
CB ''
)
2

1
(
''
=
CA
AC
=
=
So sánh các tỉ số
Tiết 41 KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
2
1
4
2''
==
AB
BA
2
1
6
3''
==
BC
CB
2
1
5
5.2''
==
CA

AC
⇒
A
B
C
4
6
5
A’
B’
C’
2
3
2.5

BC
CB ''
AB
BA ''
=
=
AC
CA ''
a/ Định nghĩa
Tiết 41 :KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
Δ A’B’C’ đồng dạng với Δ ABC nếu :
A’ = A;
B’ = B;
C’ = C
BC

CB ''
AB
BA ''
=
=
AC
CA ''
= k gọi là tỉ số đồng dạng
1/ Tam giác đồng dạng
Kí hiệu : ΔA’B’C’ ΔABC
S
~
A’
B’
C’
A
B
C

ΔA’B’C’ = ΔABC thì ΔA’B’C’ có đồng dạng với ΔABC không?
Tỉ số đồng dạng là bao nhiêu ?
A’
B’
C’
A
B
C
Em có nhận xét gì về quan hệ giữa ΔA’B’C’ , ΔABC ?
ΔA’B’C’ = ΔABC (c.c.c)
Bài tập 1 : Cho hai tam giác

ΔA’B’C’ = ΔABC suy ra
BC
CB ''
AB
BA ''
=
=
AC
CA ''
Suy ra : ΔA’B’C’ ΔABC
S
A’ = A ; B’ = B ; C’ = C
= 1
Tỉ số đồng dạng bằng 1

* Mỗi tam giác thì đồng dạng với chính nó
Tiết 41: KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
1/ Tam giác đồng dạng:
BC
CB ''
AB
BA ''
=
=
AC
CA ''
a/ Định nghĩa:
Δ A’B’C’ đồng dạng với ΔABC nếu :
A’ = A;
B’ = B;

C’ = C
Kí hiệu : ΔA’B’C’ ΔABC
BC
CB ''
AB
BA ''
=
=
AC
CA ''
= k gọi là tỉ số đồng dạng
b/ Tính chất:
S
B’
C’
A’
A
B
C