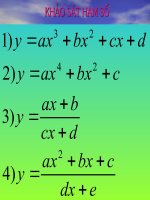Giáo án Giải tích 12 chương 1 bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số

GIÁO ÁN TOÁN 12

2013

§5 KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

I.

MỤC TIÊU:

1/ Về kiến thức:
- Biết sơ đồ khảo sát hàm số( Tìm TXĐ; xét sự biến thiên: chiều biến thiên, tìm cực
trị, tìm tiệm cận, lập bảng biến thiên; vẽ đồ thị )
- Biết vận dụng sơ đồ khảo sát hs để tiến hành khảo sát các hàm số dạng bậc 3; bậc
4( trùng phương); phân thức hữu tỉ dạng bậc nhất trên bậc nhất
- Biết cách phân loại các dạng đồ thị hàm bậc 3, bậc 4 trùng phương, hàm phân thức
dạng: y =

ax + b
. Qua đó có thể phát hiện được những sai sót khivẽ đồ thị hàm số ở từng
cx + d

loại
- Biết cách tìm toạ độ giao điểm hai đồ thị hàm số, biết giải toán biện luận số
nghiệm của pt bằng đồ thị
2/ Về kĩ năng:
3/ Về thái độ:
II.
CHUẨN BỊ :
1/ Giáo viên: Giáo án, các slides trình chiếu, phấn mầu
2/ Học sinh: Soạn trước bài , ôn tập lại cách tìm cực trị, tìm tiệm cận,

III. PHƯƠNG PHÁP:
IV.
CÁC HOẠT ĐỘNG VÀ TIẾN TRÌNH:
1/ Các hoạt động:
-

HĐ1: I.Sơ đồ khảo sát hàm số
HĐ2: II. Khảo sát hàm đa thức. Khảo sát hàm phân thức hữu tỉ dạng bậc nhất
trên bậc nhất
- HĐ3: III. Sự tương giao của các đồ thị.
2/ Thời lượng:( 6 tiết) Tiết 12 : sơ đồ khảo hàm số; khảo sát hàm số bậc 3
- Tiết 13 : Khảo sát hàm trùng phương


GIO N TON 12

2013

- Tit 14: Kho sỏt hm phõn thc hu t dng bc nht trờn bc nht
- Tit 15 : S tng giao gia cỏc th .
- Tit 16; 17 Bi tp

3/ Tin trỡnh: Tit 12
Hot ng1:
Hot ng ca thy

Hot ng ca
trũ

Ghi bng

+ GV t chc cho HS c sgk
+ HS c sgk
s kho sỏt hm s trang 31 ghi nh cỏc
bc lm toỏn
kho sỏt v v
th hm s

I. S kho sỏt hm s

+ GV cho HS lm H1

+ HS lm H1
theo hng dn
ca GV

II. KHO ST MT S HM
A THC V HM PHN
THC

- HS tr li cõu
hi, nhn xột
cõu tr li ca
bn

- Chiếu kết quả về tính biến thiên
và đồ thị của hs y = ax+b và đồ thị
hs y = ax2+bx+c

- Nờu s bin thiờn v th ca

hai hm s ó hc y = ax+b v y
= ax2+bx+c
- GV chiu kt qu tớnh bin
thiờn v th hai hs trờn
- Kim tra kt qu trờn bng
kho sỏt theo s va hc

- HS:
* Hm s y=
ax+b
- TX: R
- S bin
thiờn:
. Chiu bin
thiờn : y =a

Sgk - 31


GIÁO ÁN TOÁN 12
- Với a>0
; hs luôn đồng
biến
- Với
a<0: hs luôn
nghịch biến;
- Với a
=0 : hs luôn
không đổi bằng
b với mọi x

- Đồ thị:
( đồ thị 3
trường hợp)
* Hàm số y =
ax2+bx+c
-TXĐ: R
- Sự biến
thiên:
. Chiều biến
thiên:
- Với a
=0 b≠ 0 hàm số
là hs bậc nhất
- Với a ≠
0 ; y’ = 2ax +b
+ a>0 (
bảng BT, đồ
thị)
+ a<0 (

2013


GIÁO ÁN TOÁN 12

2013

bảng BT, đồ
thị)

+ Cho HS đọc sgk vd1

+ HS đọc vd 1
1. Hàm số y = ax3+bx2+cx+d
sgk; theo dõi
VD1: (sgk)
trình tự các
bước làm, kiểm
tra lại theo trình
tự của sơ đồ ks

+ Cho HS làm HĐ2

+ HS khảo sát
và vẽ đồ thị
hàm số trong
HĐ2

- GV đi kiểm tra uốn nắn các
bước giải của hs
- Nhận xét HĐ của HS
- Chiếu kết quả HĐ2

+ Nêu nhận xét:
Đồ thị hai hs
đối xứng qua
oy

+ Cho HS đọc sgk VD2

+ HS đọc sgk
VD2

+ Cho HS làm HĐ3:

+ HS làm HĐ3

- Gọi 1 HS lên bảng trình bày,
HS cả lớp cùng làm

- Nhận xét lời
giải của bạn,
sửa chữa theo ý
chủ quan của
mình

- GV theo dõi kiểm tra
- Chiếu lời giải HĐ3

- Chiếu kết quả khảo sát và vẽ đồ
thị hs y = - x3+3x2-4

- So sánh lời
giải của mình
với lời giải của
GV để sửa chữa

VD2: ( sgk)

+ Chiếu lời giải HĐ3

GIÁO ÁN TOÁN 12
Củng cố: Cách khảo sát và vẽ
đồ thị hàm số
3

2013

+ HS nghe ghi
+ Chiếu bảng tóm tắt đồ thị hàm
bậc 3

2

y = ax +bx +cx+d. Nêu các
trường hợp có thể xảy ra và
chiếu bảng tóm tắt dạng của đồ
thị ( như sgk trang 35)

* Hướng dẫn học ở nhà:
- Học thuộc sơ đồ khảo sát, xem
kĩ sgk về các vd khảo sát hs bậc
3, bảng tóm tắt
- Làm BT 1sgk- 43
- Đọc và chuẩn bị trước mục 2
Đ5

Tiết13
+ Kiểm tra sĩ số

+ Kiểm tra bài cũ:
* Câu hỏi: Nêu sơ đồ khảo sát
hs

+ HS lên bảng
trả lời câu hỏi;

* Bài tập: 2 HS lên bảng làm
bài ;1a; 1b

+ 2 HS làm bài
tập

-Gọi HS nhận xét; chữa bài

+ HS nhận xét
2. Hàm số y= ax4+bx2+c (a≠ 0)

+ GV cho HS đọc vd3 trong sgk

+ HS đọc vd3
sgk


GIÁO ÁN TOÁN 12

+ GV cho HS làm HĐ4
- Khảo sát và vẽ đồ thị hsố
y= - x4+2x2+3
- Gọi 1 HS lên khảo sát

- GV kiểm tra, giúp HS
thực hiện khảo sát hs trùng
phương, sửa cho HS những kĩ
năng trong khảo sát
- Chiếu kết quả khảo sát
- Dùng đồ thị biện luận số
nghiệm pt - x4+2x2+3 = m

+ HS thực hiện
HĐ4:
- HS khảo sát
hs
y= - x4+2x2+3
- 1HS lên bảng
trình bày

- Chiếu kết quả khảo sát hàm số y=
- x4+2x2+3

- So sánh với
kết quả khảo sát
của thày để rút
kinh nghiệm

? Câu hỏi: Nêu cách vẽ đồ thị
hs: y = m ( m là hằng số )
- GV: Chiếu đồ thị bằng phần
mềm Geoskepab yêu cầu Hs
nhận xét số giao điểm của đồ thị
hs : y= - x4+2x2+3

- Chiếu tương giao đồ thị

Và đường thẳng y= m . Rút ra
kết quả biện luận pt
* GV : Nêu kết luận cách giải
bài toán “ biện luận số nghiệm
pt bằng đồ thị”

2013

- HS quan sát
đồ thị
- Trình bày lời
giải biện luận
nghiệm của pt


GIÁO ÁN TOÁN 12

+ Hs nghe, ghi
nhớ
+ GV cho HS đọc vd4 sgk

+ HS làm vd 4

+ GV cho HS làm bài tập:

+ HS làm bài
tập

- Chiếu kết quả bài tập

- Khảo sát và vẽ đồ thị hàm số: y
= -x4- 2x2
- 1HS lên bảng
trình bày
- Gọi Hs lên bảng trình bày
- HS nhận xét
- Yêu cầu cả lớp làm bt
chữabài
- Nhận xét bài làm của học sinh
- Chiếu kết quả

Củng cố:

+ HS nghe

- GV củng cố lại sơ đồ khảo sát
hàm trùng phương:
- Lưu ý khi xét dấu y’ là hàm
bậc 3
- Kết luận về dạng của đồ thị
hàm số y= ax4+ bx2+c ( a≠0)
- Chiếu kết luận đồ thị

Hướng dẫn học ở nhà:
- Đọc cách khảo sát hàm số dạng

2013

GIÁO ÁN TOÁN 12

y=

2013

ax + b
cx + d

- Làm bài tập 2sgk -43
Tiết: 14
+ Kiểm tra sĩ số
+ Kiểm tra bài cũ:
- gọi 2 HS lên bảng làm bài tập
2a; 2b

+ 2 HS lên
bảng làm bài
tập 2a; 2b

- GV kiểm tra vở bài tập của một
số HS
+ Hs dưới lớp
theo dõi cho
- Gọi HS nêu sơ đồ khảo sát hs
nhận xét kết
quả
3. Hàm số y =
+ Gv cho HS đọc vd 5; 6

- Tổ chức cho học sinh đọc,
nghiên cứu ví dụ 5;6 theo nhóm.

+ HS đọc ví dụ
5; 6

- Đọc, nghiên
cứu ví dụ 5; 6
- Định hướng: Khảo sát vẽ đồ thị
theo nhóm
của hàm theo sơ đồ khảo sát hàm
được phân
số.
công.
- Phát vấn kiểm tra sự đọc hiểu
của hs

- Phát biểu nêu
khúc mắc cần
giải quyết.
- Trả lời câu hỏi
của giáo viên.

+ Khảo sát hàm số y = f(x) =

≠ 0)

ax + b
( c≠0; ad- bc
cx + d

GIÁO ÁN TOÁN 12

2013

x −1
. Sử dụng đồ thị để biện
x +1
luận theo k số nghiệm của
phương trình:

x −1
= k.
x +1

Củng cố :

+ Hs nghe ghi

y=

+ Giáo viên chiếu bảng tổng kết
các dạng của đồ thị hàm số
y=

+ Chiếu slides dạng đồ thị hàm số
ax + b
(c≠0; ad- bc ≠ 0)
cx + d

ax + b
( c≠0; ad- bc ≠ 0)
cx + d

Bài tập:
+ GV cho HS làm bài tập 3sgk
trang 43 ( Chia làm hai nhóm :
nhóm 1 làm bài 3a; nhóm hai
làm bài 3b)
+ Gọi đại diện hai nhóm lên
bảng trình bày;
+ GV chữa bài
Hướng dẫn học ở nhà:
- Đọc kĩ vd trong sgk
- Làm bài tập còn lại trong sgk
- Làm bài tập 1.24; 1.25 SBT

Tiết: 15

Bài làm của HS trên bảng
+ Hs làm bài
tập 3a; 3b theo
nhóm
+ Đại diện
nhóm lên bảng
+ Nhận xét


GIÁO ÁN TOÁN 12

2013

+ Kiểm tra sĩ số
+ Kiểmtra bài cũ:
+ GV gọi 2HS lên bảng khảo sát + 2HS lên bảng
và vẽ đồ thị hs :
làmbài tập
a) y= -x3+3x+1
x−2
b) y =
x +1

+ HS cả lớp
cùng làm

+ GV kiểm tra vở bài tập của HS + HS nhận xét
chữa bài

+ GVnêu vấn đề: ở lớp 9 ta đã
biết cách tìm toạ độ giao điểm
của hai đường thẳng ax+by=c và
a’x+b’y= c’ là đi giải hệ pt

III/ Sự tương giao của các đồ thị

 ax + by = c
. nghiệm của hệ

a ' x + b ' y = c '

Hàm số y=f(x) có đồ thị (C1); hàm
số y= g(x) có đồ thị (C2) .

chính là toạ độ giao điểm của hai
đường thẳng. Lớp 10 ta cũng
biết cách tìm hoành độ giao
điểm của đường thẳng y =ax+b
và parabol y = px2+qx+r là tìm
nghiệm của pt :

+ Để tìm toạ độ giao điểm của (C1);
(C2) ta đi giải pt: f(x)= g(x) . giả sử
pt có các nghiệm x1; x2;... khi đó toạ
độ giao điểm của (C1); (C2) là (x1;
f(x1)); (x2;f(x2))...

px2+qx+r = ax+b
+ Hãy áp dụng cách giải đã biết
để tìm hoành độ giao điểm của
hai đường y =x2+2x-3 và y=-x2x+2
+ GV khẳng định cách làm đó
vẫn đúng đối với đồ thị hai hàm
số bất kì y =f(x) và y= g(x)
+ HS làm hoạt


2013

GIÁO ÁN TOÁN 12

động 6

+ Cho HS đọc vd 7; 8
GV giải thích những thắc mắc
của HS

+ HS đọc vd 7;
vd8 đưa ra câu
hỏi thắc mắc
nếu có

+ GV chiếu quan hệ hai hàm số
y=x3+3x-2 và y=m bằng phần
mềm skeppab

+ Cho học sinh làm bài tập 4 sgk + HS làm bài
theo hai nhóm
tập 4a; 4b theo
nhóm
+ HD a) Cách 1: khảo sát và vẽ
đồ thị của hàm số y= x3-3x2+5
rồi suy ra số giao điểm với trục
Ox
- Cách 2: khảo sát và vẽ đồ thị
hàm số y= x3-3x2 , sau đó tìm
giao điểm của đồ thị với đường
thẳng y =5

+ Chiếu slides quan hệ đồ thị hai
hàm số y=x3+3x-2 và y=m

10

8

6

4

f ( x) = ( x3-3⋅x2) +5
2

-5

5

10

đồ thị hàm số y= x3-3x2+5
6

4

Tương tự với câu b)

2

-5

5

-2

-4

Đồ thị hàm số y=x3-3x2 và đường
thẳng y=5


GIÁO ÁN TOÁN 12
+ GV cho HS làm bài tập 5 sgk

+ HS làm bài
tập 5 a

4

- Gọi HS lên bảng làm câu a) Gv
kiểm tra, hướng dẫn HS yếu
- 1 HS lên bảng

2

-5

- GV HD câu b)

- nhận xét lời
giải, chữa bài

- Đưa pt đã cho thành

-4

- Khảo sát và vẽ đồ thị (C)
hàm số y = -x3+3x+1
- Tìm số giao điểm của
(C)với đường thẳng y =m+1

Củng cố: cách tìm toạ độ giao
điểm hai đường

+ HS nghe ghi

- Cách giải bài toán tìm tham số
liên quan đén số nghiệm của pt
bằng đồ thị
Hướng dẫn học ở nhà:
- Làm bài tập 6;7;8;9 sgk

Tiết 16; 17:
Hoạt động của thày
+ Kiểm tra sĩ số:
+ Kiểm tra: GV Kiểm
tra vở bài tập của HS

Bài tập

Hoạt động của trò

5

-2

- HS đứng tại
chỗ giải câu b

- x3+3x+1= m+1

2013

Ghi bảng


GIÁO ÁN TOÁN 12
1. Bài tập 6:
+ GV chiếu đề bài
+ Gọi HS đọc đề bài
Câu hỏi:Nêu cách giải
câu a) của bài toán

+ Học sinh đọc đề bài

2013

Bài 6:

+ Hs trả lời câu hỏicủa
 m
a) TXĐ: R\ − 
GV

 2
- TXĐ

y’=

- Tính y’

m2 + 2
m
⇒ y ' > 0 ∀m ∈ R, ∀x ≠ −
2
(2 x + m)
2

+ HS đứng tại chỗ giải,
GV trình bày

- CM y’ > 0 trên các
khoảng xác định với
mọi m

vậy hàm số luôn đồng biến trên các
khoảng xác dịnh với mọi m

+ Gọi HS nêu cách giải
câub)

+ Tìm tiệm cận đứng

b) Giải :

+ Gọi 1HS đứng tại
chỗ giải

+ Thay toạ độ của
điểm A vào pt của
tiệm cận đứng để tìm
m

limm

x →−

2

mx − 1
= +∞ ⇒ x = − m là tiệm
2x + m
2

cận đứng
- Để tiệm cận đứng đi qua điểm
A(-1; 2 ) thì −

+ Gọi 1Hs lên giải câu
c).HS cả lớp cùng giải

m
= −1 ⇔ m = 2
2

+ 1HS lên bảng giải
câu c)
+ HS cả lớp giải

1. Bài tập 7
+ Gọi Hs đọc đề bài
+ Gọi Hs nêu cách giải

+ 1HS đọc đề bài

a) TXĐ:R

+ HS nêu cách giải

+ Đồ thị của hs đi qua điểm (-1;1) nên

- TXĐ

ta có 1=

+ Gọi 1Hs đứng giải tại
- Thay toạ độ của
chỗ
điểm vào pt của hàm
số để tìm m

1 1
1
+ +m ⇒m=

4 2
4


GIÁO ÁN TOÁN 12

2013

+ HS đứng giải

+ Gọi Hs lên khảo sát
và vẽ đồ thị của hs với
m=1

+ HS lên bảng giải
+ HS dưới lớp làm

- cho Hs dưới lớp làm
GV chấm bài cho
những Hs làm nhanh
nhất

+ Gọi HS Nêu cách giải
bài toán

+ HS nêu cách giải
- Tìm hoành độ tiếp
điểm; toạ độ tiếp điểm
M

+ ĐiểmM thuộc đồ thị có tung độ là
có hoành độ là nghiệm của pt :
1 4 1 2
7
x + x +1 =
4
2
4

- Viết pt tiếp tuyến với
Giải ta được x=-1 và x=1
đồ thị tại M
Vậy ta có hai điểm thuộc đồthị có
tungđộ bằng

7
7
là M(-1; ) vàM’ (1;
4
4

7
)
4

Ta có y’(-1)=-2; y’(1)=2
Suy ra pt tiếp tuyến cần tìm là :
7
4

y- =y’(-1)(x+1)⇔ y=-2xvà y-

2. Bài tập 8

+ 1HS đọc đề bài

1
4

7
1
= y’(1)(x-1)⇔ y= 2x4
4

a) TXĐ:R

7
4


2013

GIÁO ÁN TOÁN 12
Gọi HS đọc đề bài

+HS nêu cách giải

? Nêu cách giải câu a)

- TXĐ

y’= 3x2+2(m+3)x

- Tính y’, cho y’=0
tìm x

x = 0
y’=0⇔ 
 x = − 2m + 6
3


- Lập bảng biến thiên

Gv Lưu ý: Tuy cách
giải trên là tổng quát
nhưng hàm số có cực
đại tại x=-1 nên điểm
cực đại phải chứa tham
số m và ta có bảng BT
như trên. cách giải 2
ngắn gọn hơn nhiều

Từ bảng biến thiên
cho điểm cực đại bằng
-1 tìm m
- Hoặc dùng điều kiện:
Để hs có cực đại tại
 y '(−1) = 0
 y ''(−1) < 0

x=-1 thì 

+ Bảng biến thiên:
x

-∞

−

2m + 6
3

0

+∞
y’

+

0

-

0

y
+∞

-∞

Hàm số đạt cực đại tại x=-1 ⇔
−

+ gọi Hs nêu cách giải

+ HS nêu cách giải:

+ gọi HS lên bảng làm
câu b)

- hs cắt trục hoành tại
x=-2 khi pt: x3+
(m+3)x2+1-m =0 có
ngiệm bằng -2
- Thay x=-2 vào pt
giải tìm m
+ HS làm câu b)
ĐS: m= −

5
3

2m + 6
3
=-1 ⇔ m= −
3
2

+

GIÁO ÁN TOÁN 12
3. Bài tập9
+ Gọi HS lên bảng giải;
HS cả lớp cùng làm

+ HS giải Bt 9.
+ HS lên bảng giải bài
tập
a) ĐS: m=0
b) Khảo sát hàm số
y=

x +1
x −1

c) Giao với trục tung
là M(0;-1)
y’(0)=-2, PT tt là
y+1=-2x hay y=-2x- 1

2013