25 câu hỏi trắc nghiệm ôn tập đồ thị của hàm số bậc 4 file word có lời giải chi tiết

Câu 1.

[2D1-2] Bảng biến thiên sau của hàm
số nào?
y = x 4 − 3x 2 − 3.
A.
1
y = − x 4 + 3 x 2 − 3.
4
B.
y = x 4 − 2 x 2 − 3.
C.
y = x 4 + 2 x 2 − 3.
D.
Lời giải
Chọn C.

y′ = 4 x − 4 x
Ta có:
, cho
Bảng biến thiên:
3

Câu 2.

x = 0
y′ = 0 ⇒ 4 x3 − 4 x = 0 ⇔ 
 x = ±1

[2D1-2] Bảng biến thiên ở bên là của hàm số nào?
y = x 4 − 3 x 2 + 1.

A.
y = − x 4 + 3x 2 + 1.
B.
y = x 4 + 3x 2 − 1.
C.
y = − x 4 − 3x 2 + 1.
D.

Lời giải
Chọn C.

– Website chuyên đề thi – tài liệu file word mới nhất


y′ = 4 x3 + 6 x
Ta có:
Bảng biến thiên:

Câu 3.

y′ = 0 ⇒ 4 x3 + 6 x = 0 ⇔ x = 0
, cho

[2D1-2] Bảng biến thiên ở bên là của
hàm số nào?
y = − x 4 − 3 x 2 − 3.
A.
y = x 4 − x 2 − 3.
B.
y = x 4 − 2 x 2 − 3.

C.
y = x 4 + 2 x 2 − 3.
D.
Lời giải
Chọn C.

y′ = 4 x3 − 4 x
Ta có:
Bảng biến thiên:

Câu 4.

, cho

[2D1-2] Cho hàm số

x = 0
y′ = 0 ⇒ 4 x3 − 4 x = 0 ⇔ 
 x = ±1

y = f ( x)

liên tục trênvà có bảng biến thiên như hình vẽ.

Khẳng định nào sau đây là sai?

– Website chuyên đề thi – tài liệu file word mới nhất


A. Hàm số có hai điểm cực tiểu, một điểm cực đại.

B. Hàm số có giá trị nhỏ nhất bằng −4.
C. Hàm số đồng biến trên khoảng (1; 2).
D. Hàm số có giá trị lớn nhất bằng −3.
Lời giải
Chọn A.
Dựa vào bảng biến thiên hàm số không có giá trị lớn nhất.
Câu 5.

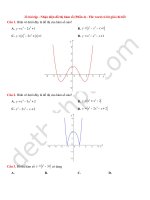
[2D1-2] Đồ thị hình bên là của hàm số nào?
y = − x 4 + 3x 2 + 1.
A.
y = x 4 − 2 x 2 + 1.
B.
y = − x 4 + 2 x 2 + 1.
C.
y = x 4 + 3x 2 + 1.
D.

Lời giải
Chọn C.

Đồ thị hàm số có

a<0

, có 3 điểm cực trị nên

b>0

( 1; 2 )

và có điểm cực đại

nên chọn đáp án

C.
Câu 6.

[2D1-2] Đồ thị hình bên là của hàm số nào?

y = x4 + 2 x2 .
A.

y = x4 − 2x2.
B.

y = − x4 + 2x2 .
C.

y = − x4 − 2x2.
D.

– Website chuyên đề thi – tài liệu file word mới nhất


Lời giải
Chọn B.
Đồ thì hàm số quay lên nên

a>0

.

Đồ thị hàm số có ba điểm cực trị nên

b<0

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ

bằng

0

nên

c=0
Câu 7.

[2D1-2] Đồ thị hình bên là của hàm số nào?
y = − x 4 + 4 x 2 − 1.
A.
y = x 4 − 2 x 2 − 1.
B.
y = x 4 − 2 x 2 + 1.
C.
y = x 4 − 4 x 2 − 1.
D.

Lời giải

Chọn B.
Đồ thì hàm số quay lên nên

a>0

.

Đồ thị hàm số có ba điểm cực trị nên

b<0

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ

bằng

c = −1

Câu 8.

nên
[2D1-2] Đồ thị hình bên là của hàm số nào?
y = x 4 + 2 x 2 − 1.
A.

– Website chuyên đề thi – tài liệu file word mới nhất

−1

y = − x 4 − 2 x 2 − 1.
B.

y = x 4 + 2 x 2 + 1.
C.

y = − x 4 + 2 x 2 − 1.
D.

Lời giải
Chọn A.
Đồ thì hàm số quay xuống nên

a<0

Đồ thị hàm số có ba điểm cực trị nên
Câu 9.

.

b>0

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
[2D1-2] Đồ thị hình bên là của hàm số nào?
y = x 4 − 3x 2 − 3.
A.
1

y = − x 4 + 3 x 2 − 3.
4
B.
y = x 4 − 2 x 2 − 3.
C.
y = x 4 + 2 x 2 − 3.
D.

−1

nên

c = −1

Lời giải

– Website chuyên đề thi – tài liệu file word mới nhất


Chọn C.
Đồ thì hàm số quay lên nên

a>0

.

b<0

Đồ thị hàm số có ba điểm cực trị nên
Câu 10.

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
[2D1-2] Đồ thị hình bên là của hàm số nào?
y = x 4 − 3x 2 .
A.
1
y = − x 4 + 3x 2 .
4
B.
y = − x4 − 2x2 .
C.
y = − x4 + 4 x2.
D.

−3

nên

c = −3

Lời giải
Chọn D.
Đồ thì hàm số quay xuống nên

a<0

Đồ thị hàm số có ba điểm cực trị nên

.

b>0

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
Câu 11.

0

nên

c=0

[2D1-2] Đồ thị hình bên là của hàm số nào?
y = x 4 − 3 x 2 − 1.
A.
1
y = − x 4 + 3x 2 − 1.
4
B.
y = x 4 + 2 x 2 − 1.
C.
y = x 4 − 2 x 2 − 1.
D.

– Website chuyên đề thi – tài liệu file word mới nhất

Lời giải
Chọn A.
Đồ thì hàm số quay lên nên

a>0

.

Đồ thị hàm số có một điểm cực trị nên

b≥0

.
−1

Câu 12.

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
nên
y = ax 4 + bx 2 + c
[2D1-4] Đồ thị hàm số
cắt trục hoành

c = −1

A, B, C , D

tại bốn điểm
rằng

AB = BC = CD

phân biệt như hình vẽ bên. Biết
, mệnh đề nào sau đây là đúng?

a > 0, b < 0, c > 0, 100b2 = 9ac
A.

.

a > 0, b > 0, c > 0, 9b 2 = 100ac
B.

.

a > 0, b < 0, c > 0, 9b 2 = 100ac
C.

.

a > 0, b > 0, c > 0, 100b 2 = 9ac
D.

.

Lời giải
Chọn A.
Đồ thì hàm số quay lên nên

a>0

.

Đồ thị hàm số có ba điểm cực trị nên

b<0

.

Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên

(

A − x1 ; 0
Đồ thị hàm số cắt trục hoành tại 4 điểm

) B( −
,

c>0
x2 ; 0

.

) C(
,

x2 ; 0

)

A
và

(

x1 ; 0

– Website chuyên đề thi – tài liệu file word mới nhất

)

.


Mà

AB = BC = CD ⇔ − x1 + x2 = 2 x1 ⇔ x2 = 3 x1 ⇔ x2 = 9 x1

Khi đó:

.

b
b


 x1 + x2 = − a
 x1 = − 10a



c
9b


⇔  x2 = −
 x1 x2 =
a
10a


 x2 = 9 x1
 x1 x2 = c
b 9b
⇔
.
= c ⇔ 9b 2 = 100ac




10a 10a
y = f ( x) = ax 4 + bx 2 + c

Câu 13.

[2D1-3] Biết rằng hàm số

có đồ thị là đường cong như hình vẽ bên.

f ( a + b + c)

Tính giá trị

.

B A. f (a + b + c ) = −1 .

B.
C.

D.

f (a + b + c) = 2

.

f ( a + b + c ) = −2

f ( a + b + c) = 1

.

.

Lời giải
Chọn A.
Dựa vào đồ thị hàm số ta có: điểm cực tiểu và cực đại của đồ thị hàm số là

Ta có:

A ( 1; −1) B ( 0;1)
,
.

y′ = 4ax 3 + 2bx

– Website chuyên đề thi – tài liệu file word mới nhất


a + b + c = −1 a = 2


c =1
⇔ b = −4 ⇒ y = 2 x 4 − 4 x 2 + 1
Do đó: 
4a + 2b = 0
c = 1



Mà

a + b + c = −1 ⇒ f ( a + b + c ) = f ( −1) = −1

y = ax 4 + bx 2 + c
Câu 14.

[2D1-3] Cho hàm số

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là

đúng?
a > 0, b < 0, c > 0
A.
.
a < 0, b > 0, c < 0
B.
.
a > 0, b > 0, c > 0
C.
.
a > 0, b < 0, c < 0
D.
.

Lời giải.
Chọn B.

Câu 15.

a < 0, b > 0

c<0
Dựa vào đồ thi hàm số ta có:
(do hàm số có 3 cực trị ) và
.
4
2
y = ax + bx + c

[2D1-3] Cho hàm số
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là
đúng?
a > 0, b < 0, c < 0
A.
.
a < 0, b > 0, c > 0
B.
.

– Website chuyên đề thi – tài liệu file word mới nhất


a > 0, b > 0, c > 0

C.

a > 0, b < 0, c > 0

D.

.
.

Lời giải.
Chọn D.

Câu 16.

a > 0, b < 0

c>0
Dựa vào đồ thi hàm số ta có:
(do hàm số có 3 cực trị ) và
.
4
2
y = ax + bx + c
Cho hàm số
có đồ thị như hình vẽ bên. Kết luận nào sau đây là đúng?
a < 0, b ≤ 0, c > 0
A.
.
a < 0, b < 0, c < 0
B.
.
a > 0, b > 0, c > 0
C.
.
a < 0, b > 0, c ≥ 0
D.
.

Lời giải.
Chọn A.

a < 0, b ≤ 0

c>0
(do hàm số có 1 cực trị ) và
.

y = f ( x)
¡
[2D1-3] Cho hàm số
liên tục trên có đồ thị (C) như hình vẽ bên. Khẳng định nào
Dựa vào đồ thi hàm số ta có:

Câu 17.

sau đây là đúng?
A. Đồ thị (C) có ba điểm cực trị tạo thành một tam giác cân.
B. Giá trị lớn nhất của hàm số là 4.

– Website chuyên đề thi – tài liệu file word mới nhất


C. Tổng các giá trị cực trị của hàm số bằng 7.
D. Đồ thị (C) không có điểm cực đại nhưng có hai điểm cực
( −1;3) ( 1;3)
tiểu là
và
.

Lời giải.
Chọn A.
Dựa vào đồ thị hàm số ta thấy:
+ 3 điểm cực trị của đồ thị hàm số tạo thành 1 tam giác cân.
+ Hàm số không có giá trị lớn nhất.
+Tổng các giá trị cực trị của hàm số là 10.
+ Hàm số có 1 cực đại và 2 cực tiểu.
y = f ( x)

Câu 18.

[2D1-2] Cho hàm số

m

tham số
để phương trình
−4 < m < −3
A.
.
−4 ≤ m ≤ −3
B.
.
−6 ≤ m ≤ −5
C.
.
−6 < m < −5
D.
.

có đồ thị (C) như hình vẽ bên. Tìm tất cả các giá trị thực của
f ( x) = m + 2

có bốn nghiệm phân biệt.

Lời giải.
Chọn D.

– Website chuyên đề thi – tài liệu file word mới nhất


y = f ( x)

f ( x) = m + 2

Số nghiệm của phương trình

là số nghiệm của hai đồ thị hàm số

và

y = m + 2.

đường thẳng
Dựa vào đồ thị hàm số, ta thấy 2 đồ thị hàm số có 4 giao điểm

⇔ −4 < m + 2 < −3 ⇔ −6 < m < −5

f ( x) = ax 4 + bx 2 + c
Câu 19.

[2D1-2] Cho hàm số

có đồ thị của hàm số như hình vẽ bên. Kết luận nào

sau đây là đúng?
a > 0, b < 0, c > 0
A.

.
a < 0, b < 0, c > 0
B.
.
a < 0, b > 0, c > 0
C.
.
a < 0, b > 0, c < 0

D.

.

Lời giải.
Chọn C.

Câu 20.

a < 0, b > 0, c > 0

Dựa vào đồ thị hàm số ta có:
y = f ( x ) = ax 4 + bx2 + c
[2D1-1] Cho hàm số
có bảng biến thiên như hình vẽ dưới đây.

Khẳng định nào sau đây sai?

¡
4
A. Giá trị lớn nhất của hàm số trên

bằng .
B. Hàm số có hai điểm cực đại và một điểm cực tiểu.

– Website chuyên đề thi – tài liệu file word mới nhất


Oy

C. Đồ thị hàm số nhận trục
là trục đối xứng.
ab ( c + 1)
D. Biểu thức
nhận giá trị dương.
Lời giải.
Chọn D.
⇒ ab < 0
Dựa vào BBT, ta thấy hàm số có 3 cực trị
.
O ( 0;0 ) ⇒ c = 0
Đồ thị hàm số đi qua gốc tọa độ
.
ab ( c + 1) = ab < 0 ⇒
Vậy
Khẳng định D sai.
y = f ( x ) = ax 4 + bx 2 + c
[2D1-3] Đồ thị hàm số
như hình vẽ dưới đây. Khẳng định nào sau đây

Câu 21.

là đúng ?
a > 0; b > 0; c > 0; b2 = 4ac
A.

.
a > 0; b < 0; c > 0; b = 4ac
2

B.

.
a > 0; b > 0; c > 0; b > 4ac
2

C.

.
a > 0; b > 0; c > 0; b < 4ac
2

D.

.
Lời giải.

Chọn B.
Dựa vào đồ thị hàm số, ta nhận xét
Dựa vào 4 đáp án, ta chọn B.

a>0

và

ab < 0 ⇒ b < 0

(Do hàm số có 3 cực trị)

y = ax 4 + bx2 + c
Câu 22.

[2D1-4] Hình vẽ bên là đồ thị của hàm số
A = a 2 + b2 + c 2

A.
B.
C.
D.

A = 24
A = 20

A = 18
A=6
.

. Giá trị của biểu thức

có thể nhận giá trị nào trong các giá trị sau?

.

.
.

Lời giải.

– Website chuyên đề thi – tài liệu file word mới nhất


Chọn C.
x = 0
y = ax + bx + c ⇒ y ' = 4ax + 2bx; y ' = 0 ⇔  2
x = − b
2a

4

Ta có

2

3

a < 0; b > 0

Dựa vào đồ thị hàm số, ta có

.

.

( C)

Gọi đồ thị hàm số đã cho là
. Dựa vào đồ thị hàm số ta có:
4
2
+ I ( 0; −1) ∈ ( C ) ⇒ a.0 + b.0 + c = −1 ⇒ c = −1
.
c =−1
4
2
A ( 1; 2 ) ∈ ( C ) ⇒ a.1 + b.1 + c = 2 ⇔ a + b + c = 2 ¬ 
→a + b = 3 ⇔ a = 3−b
+
.
+ Giá trị cực đại của hàm số bằng 3 nên ta có:
2

 b 
 b 
c =−1
a.  − ÷ + b.  − ÷+ c = 3 ¬ 
→ b 2 = −16a ( *)
 2a 
 2a 

Thế

( *)

vào
b = 4 ⇒ a = −1

ta được:

b = 4
b 2 − 16b + 48 = 0 ⇔ 
b = 12

.
A = a 2 + b2 + c2 = 18 ⇒

a<0
(thỏa mãn điều kiện
). Khi đó
Chọn C.
4
2
y = f ( x ) = ax + bx + c
[2D1-4] Hàm số
có bảng biến thiên như hình vẽ dưới đây.
Với

Câu 23.

a = 3−b

.

P = 2+ 2b + 3c
Tính giá trị của biểu thức
P = −15
P = 15
A.
.
B.
.

P = −8
C.
.
Lời giải.

D.

P=8

.

Chọn A.
y = ax 4 + bx2 + c ⇒ y ' = 4ax 3 + 2bx;
Ta có
.

– Website chuyên đề thi – tài liệu file word mới nhất


( C)

Câu 24.

Gọi đồ thị hàm số đã cho là
. Dựa vào BBT ta có:
4
2
+ I ( 0; −3) ∈ ( C ) ⇒ a.0 + b.0 + c = −3 ⇒ c = −3 ( 1)
.
x = ±1 ⇒ y ' ( 1) = 0 ⇔ 4 a + 2b = 0 ( 2 )
+ Hàm số đạt cực tiểu tại
.
yCD = −5 ⇒ a + b + c = −5 ( 3)
+ Hàm số có cực đại
.
( 1) , ( 2 ) , ( 3)
a = 2, b = −4, c = −3
P = 2+ 2b + 3c = −15
Giải hệ
ta được:
. Vậy
.
y = f ( x)
¡
[2D1-3] Cho hàm số
liên tục và xác định trên
và có đồ thị như hình vẽ dưới đây.

( 0;1)
(I). Hàm số nghịch biến trên

.

(II). Hàm số đồng biến trên
(III). Hàm số có ba điểm cực trị.

.

( −1; 2)

2
(IV). Hàm số có giá trị lớn nhất bằng .
Số mệnh đề đúng trong các mệnh đề trên là
1
A. .
2
B. .
3
C. .
4
D. .

Câu 25.

Lời giải.
Chọn B.
Dựa vào đồ thị hàm số, ta thấy:
( −∞; −1)
( 0;1) ⇒
+ Hàm số nghịch biến trên
và

(I) đúng.
( −1;0 )
( 1; +∞ ) ⇒
+ Hàm số đồng biến trên
và
(II) sai.
⇒
+ Hàm số có 3 điểm cực trị
(III) đúng.
⇒
+ Hàm số không có giá trị lớn nhất
(IV) sai
Vậy số các mệnh đề đúng là 2.
y = f ( x)
¡
[2D1-2] Cho hàm số
liên tục trên
và có bảng biến thiên như hình vẽ. Tìm tất cả

các giá trị thực của

m

f ( x ) = 2m
để phương trình

có đúng hai nghiệm phân biệt.

– Website chuyên đề thi – tài liệu file word mới nhất

x
y'
y

A.

m = 0
 m < −3


−1
0
0

−∞

+

.

B.

m < −3

Chọn C.

.

-

00

10
0

+

m = 0

m < − 3

2

C.
Lời giải.

+∞
-

m<−

.

D.

3
2

f ( x ) = 2m

Số nghiệm của phương trình

y = f ( x)
chính la số giao điểm của hai đồ thị hàm số

y = 2m

và đường thẳng

.

Dựa vào BBT, ta thấy hai đồ thị hàm số giao nhau tại 2 điểm

m = 0
 2m = 0
⇔
⇔
m < − 3
2
m
<
−
3


2

.

– Website chuyên đề thi – tài liệu file word mới nhất