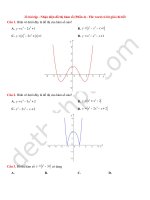
30 bài tập nhận diện đồ thị hàm số (phần 1) file word có lời giải chi tiết

30 bài tập - Nhận diện đồ thị hàm số (Phần 1) - File word có lời giải chi tiết
Câu 1. Bảng biến thiên ở bên là của hàm số nào?
�

x

�

1

y'

+

0

+

y

�
1
�

A. y  x3  3x 2  3x

B. y   x3  3x 2  3x

C. y  x3  3x 2  3x

D. y   x3  3x 2  3x

Câu 2. Bảng biến thiên ở bên là của hàm số nào?
�

x
y'

0
−

y

0

�

2
+

0

�

−

3
�

−1
A. y  x3  3x 2  1

B. y   x 3  3x 2  1

C. y  x3  3x 2  1

D. y   x 3  3x 2  1

Câu 3. Cho hàm số y  f  x  xác định, liên tục trên � và có bảng biến thiên dưới đây. KHẲNG ĐỊNH
nào sau đây là đúng?
x

�

y'

0
+

y

�

1
−

0

�

0

�

−1

A. Hàm số có đúng một cực trị
B. Hàm số có giá trị cực tiểu bằng 1
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1
D. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1

+


Câu 4. Cho hàm số y  ax 3  bx 2  cx  1 có bảng biến thiên dưới đây:
x

�

y'

x1

0
−

−

0

�

x2
+

0

−

y

Mệnh đề nào dưới đây đúng?
A. b  0, c  0

B. b  0, c  0

Câu 5. Đồ thị hình bên là của hàm số nào?
A. y  x3  3x
B. y  x3  3x
C. y   x 3  2 x
D. y   x 3  2 x

Câu 6. Đồ thị hình bên là của hàm số nào?
A. y   x 3  1
B. y  2 x3  x 2
C. y  3x 2  1
D. y  4 x 3  1

C. b  0, c  0

D. b  0, c  0

Câu 7. Đồ thị hình bên là của hàm số nào?
A. y  2 x 3  3x 2  1
B. y  2 x 3  3x 2  1
C. y  2 x 3  3x 2  1
D. y  2 x 3  3x 2  1

Câu 8. Đồ thị hình bên là của hàm số nào?
A. y  x 3  3x
B. y   x 3  3x
C. y   x 3  3x  1
D. y  x3  3x  1

Câu 9. Đồ thị hình bên là của hàm số nào?
1
A. y  x 3  x 2  x
3
1
B. y  x3  x 2  x  1
3
C. y   x 3  3x 2  3x
D. y  x 3  3x 2  3x  2


Câu 10. Đồ thị hình bên là của hàm số nào?
A. y  x 3  3x 2  3x  1
B. y   x 3  3x 2  1
C. y  x3  3x  1
D. y   x 3  3x 2  1
Câu 11. Đồ thị hàm số y   x 3  3x 2  2 có dạng

A.

B.

C.

D.

Câu 12. Đồ thị hàm số y  x 3  3x  2 có dạng

A.

B.


C.

D.

Câu 13. Đồ thị hàm số y  ax 3  bx 2  cx  d có đồ thị như hình vẽ sau.
Mệnh đề nào sau đây đúng?
A. a  0; b  0; c  0; d  0
B. a  0; b  0; c  0; d  0
C. a  0; b  0; c  0; d  0
D. a  0; b  0; c  0; d  0
Câu 14. Cho hàm số y  ax3  bx 2  cx  d có đồ thị như hình vẽ sau.
Khẳng định nào sau đây đúng?
A. a, b, c  0; d  0
B. a, b, d  0; c  0

C. a, c, d  0; b  0
D. a, d  0; b, c  0

Câu 15. Cho hàm số y  f  x  có đồ thị hàm số y  f '  x  cắt trục Ox
tại ba điểm có hồnh độ như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. f  c   f  a   f  b 
B. f  c   f  b   f  a 
C. f  a   f  b   f  c 
D. f  b   f  a   f  c 


Câu 16. Cho hàm số y  ax 3  bx 2  cx  d có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A. b  0; cd  0
B. b  0; cd  0
C. b  0; cd  0
D. b  0; cd  0

Câu 17. Cho hàm số y  ax 3  bx 2  cx  d có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0
B. a  0, b  0, c  0, d  0
C. a  0, b  0, c  0, d  0
D. a  0, b  0, c  0, d  0

Câu 18. Cho hàm số y  ax3  bx 2  cx  d có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0
B. a  0, b  0, c  0, d  0
C. a  0, b  0, c  0, d  0

D. a  0, b  0, c  0, d  0
Câu 19. Cho hàm số y  ax3  bx 2  cx  d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0
B. a  0, b  0, c  0, d  0
C. a  0, b  0, c  0, d  0
D. a  0, b  0, c  0, d  0


Câu 20. Cho hàm số y  ax 3  bx 2  cx  d có đồ thị như hình bên.
Khẳng định nào sau đây đúng?
A. a, d  0; b, c  0
B. a, b, c  0; d  0
C. a, c, d  0; b  0
D. a, b, d  0; c  0

Câu 21. Cho hàm số y  ax 3  bx 2  cx  d có đồ thị như hình bên.
Hỏi phương trình ax 3  bx 2  cx  d  1  0 có bao nhiêu nghiệm?
A. Phương trình khơng có nghiệm
B. Phương trình có đúng một nghiệm
C. Phương trình có đúng hai nghiệm
D. Phương trình có đúng ba nghiệm

Câu 22. Cho hàm số y  ax3  bx 2  cx  d có bảng biến thiên như hình vẽ dưới đây:
x

�

y'

0
+

y

0

−

0

Khẳng định nào sau đây là sai.
A. Hàm số có 2 điểm cực trị tại x  0 và x  2
B. Giá trị lớn nhất của hàm số bằng 4
C. Giá trị cực tiểu của hàm số là yCT  0
D. Hàm số có a  0; c  0

+
�

4
�

�

2

0

Câu 23. Cho đồ thị hàm số y  ax 3  bx 2  cx  d như hình vẽ bên.
Khẳng định nào sau đây là đúng.
A. a  0; b  0; c  0; d  0
B. a  0; b  0; c  0; d  0
C. a  0; b  0; c  0; d  0
D. a  0; b  0; c  0; d  0
Câu 24. Cho đồ thị hàm số y  ax 3  bx 2  cx  d như hình
vẽ bên. Khẳng định nào sau đây là đúng.
A. a  0; b  0; c  0; d  0
B. a  0; b  0; c  0; d  0
C. a  0; b  0; c  0; d  0
D. a  0; b  0; c  0; d  0

Câu 25. Cho hàm số y  ax 3  bx 2  cx  d có đồ thị của
hàm số f '  x  như hình vẽ bên. Khẳng định nào sau đây là
sai.
A. Hàm số đã cho đạt cực đại tại x  1
B. Hàm số đã cho có 2 điểm cực trị
C. f  0   f  1  f  2 
D. Hàm số đã cho nghịch biến trên khoảng  1;2 


Câu 26. Cho đồ thị hàm số y   x 3  ax 2  bx  c  a, b, c �� có đồ thị là
đường cong như hình vẽ. Tìm khẳng định sai?
A. a 2  b 2  c 2  2bac  117
B. b10  abc �0
C. c 2  100bc  1
D. a 2  4b �0
Câu
27.

Cho
đồ
thị
hàm
số
3
2
y  ax  bx  cx  d  a , b, c �� có đồ thị là đường cong
như hình vẽ. Tìm khẳng định đúng?
A. Hàm số nghịch biến trên khoảng  0;2  và  4; �
B. Hàm số đạt cực tiểu tại x  2, x  2
C. Với c � 1;2 thì f  1  f  c   f  2 
y  max y  0 .
D. xmin
� 0;2
x� 1;2
Câu 28. Đường cong ở hình bên là đồ thị của hàm số y  f  x  .
Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị của hàm số y  f  x  có trục đối xứng là trục hồnh.
B. Phương trình f  x   m có đúng hai nghiệm phân biệt khi
m  2 hoặc m  2 .
C. Hàm số y  f  x  đồng biến trên khoảng  0;2 
D. Đồ thị của hàm số có hai điểm cực trị


Câu 29. Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
�

x
y'

−2
+

0

y

�

0
−

0

+
�

2
�

−1

A. Hàm số đạt cực tiểu tại x  1 và đạt cực đại tại x  3
B. Giá trị cực đại của hàm số là −2
C. Giá trị cực tiểu của hàm số là 0
D. Hàm số đạt cực đại tại x  2 và đạt cực tiểu tại x  0
3
2
Câu 30. Cho hàm số y  f  x    x  ax  bx  c xác định, liên tục trên � và bảng biến thiên như hình

vẽ
x

�

y'
y

−3
−

0

�

1
+

�

0

−

9
�

−23
Tính giá trị của biểu thức T  f  2   2. f  0 

A. 6

B. 10

C. 12

D. 8


HƯỚNG DẪN GIẢI
Câu 1. Chọn đáp án A
Hàm số luôn đồng biến nên loại B, C, D.
Câu 2. Chọn đáp án A
Đồ thị hàm số có đạt cực trị tại 2 điểm x  0; x  2 nên loại C, D. Mà nhìn vào dạng biến thiên của đồ
thị hàm số nên ta loại B.
Câu 3. Chọn đáp án D
Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1
Câu 4. Chọn đáp án C
Đầu tiên nhìn vào bảng biến thiên ta suy ra a  0 . Ta có y '  3ax 2  2bx  c có 2 nghiệm dương nên ta
2b
�
x

x


0
1
2
�

�
3a
� b  0; c  0 .
có �
c
�x x 
0
�1 2 3a
Câu 5. Chọn đáp án B
Hàm số đạt cực trị tại x  1; x  1 .
Câu 6. Chọn đáp án A
Hàm số đi qua điểm  1;2  nên A đúng.
Câu 7. Chọn đáp án D
Hàm số đạt cực trị tại x  0; x  1 và dạng của đồ thị nên D đúng.
Câu 8. Chọn đáp án A
Hàm số đạt cực trị tại x  1; x  1 và qua điểm  0;0  .
Câu 9. Chọn đáp án A
�1�
1; �.
Đồ thị hàm số qua  0;0  và �
� 3�
Câu 10. Chọn đáp án A
Đồ thị cắt trục tung tại y  1 � Loại D
Có dạng từ dưới đi lên � Loại B
Đi qua điểm  1;2  .
Câu 11. Chọn đáp án C
Đồ thị cắt trục tung tại y  2 � Loại A, D.
Có hình dạng hướng xuống khi x � �. Loại B.
Câu 12. Chọn đáp án D

Đồ thị cắt trục tung tại y  2 .
Câu 13. Chọn đáp án A
lim y  �, lim y  �� a  0

x ��

x��

Đồ thị cắt trục tung tại điểm có tung độ dương � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành
độ 2 điểm cực trị của đồ thị hàm số có tổng dương � 

b
c
 0 � b  0 và tích âm �  0 � c  0 .
a
a

Câu 14. Chọn đáp án D
lim y  �, lim y  �� a  0

x ��

x��

Đồ thị cắt trục tung tại điểm có tung độ dương � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành
độ 2 điểm cực trị của đồ thị hàm số có tổng dương � 

b
c

 0 � b  0 và tích âm �  0 � c  0 .
a
a

Câu 15. Chọn đáp án A
Ta có f '  x   0 với x � a, b  � f  a   f  b 
Mà f '  x   0 với x � b, c  � f  b   f  c  .
Câu 16. Chọn đáp án D
lim y  �, lim y  �� a  0

x ��

x ��

Đồ thị cắt trục tung tại điểm có tung độ âm � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành độ 2
điểm cực trị của đồ thị hàm số có tổng âm � 

b
c
 0 � b  0 và tích âm �  0 � c  0 .
a
a

Câu 17. Chọn đáp án A
lim y  �, lim y  �� a  0

x ��

x��

Đồ thị cắt trục tung tại điểm có tung độ dương � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành
độ 2 điểm cực trị của đồ thị hàm số có tổng dương � 

b
 0 � b  0 và tích bằng 0 � c  0 .
a

Câu 18. Chọn đáp án A
lim y  �, lim y  �� a  0

x ��

x��

Đồ thị cắt trục tung tại điểm có tung độ âm � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành độ 2
điểm cực trị của đồ thị hàm số có tổng âm � 
Câu 19. Chọn đáp án D
lim y  �, lim y  �� a  0

x ��

x��

b
 0 � b  0 và tích bằng 0 � c  0 .
a


Đồ thị cắt trục tung tại điểm có tung độ dương � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành
độ 2 điểm cực trị của đồ thị hàm số có tổng dương � 

b
 0 � b  0 và tích bằng 0 � c  0 .
a

Câu 20. Chọn đáp án D
lim y  �, lim y  �� a  0

x ��

x��

Đồ thị cắt trục tung tại điểm có tung độ dương � d  0 . Ta có: y '  3ax 2  2bx  c , nhận thấy hoành
độ 2 điểm cực trị của đồ thị hàm số có tổng âm � 

b
c
 0 � b  0 và tích âm �  0 � c  0 .
a
a

Câu 21. Chọn đáp án C
Tịnh tiến đồ thị hàm số xuống dưới 1 đơn vị theo phương song song trục Oy, dễ thấy đồ thị lúc này chỉ
cắt Ox tại đúng 2 điểm.
Câu 22. Chọn đáp án B
Dựa vào bảng biến thiên suy ra hàm số đã cho có 2 điểm cực trị tại x  0; x  2 .
Giá trị cực đại là 4, giá trị cực tiểu là 0
y  �� a  0 , mặt khác xCT .xCD  c  0 � c  0 .
Do xlim
��

3a
Câu 23. Chọn đáp án B
y  � nên a  0 ; đồ thị hàm số cắt trục Oy tại điểm  0; d  � d  0 .
Ta có xlim
��
�xCD  xCT  0
; y '  3ax 2  2bx  c
Đồ thị hàm số có 2 điểm cực trị và ta thấy �
�xCD .xCT  0
�
�
 '  b 2  3ac  0
�
�2b
Khi đó �  0 � b  0 (do a  0 ).
�3a
�c
0�c 0
�
�3a
Câu 24. Chọn đáp án B
y  � nên a  0 ; đồ thị hàm số cắt trục Oy tại điểm  0; d  � d  0 .
Ta có: xlim
��
Đồ thị hàm số có 2 điểm cực trị và 2 điểm này đều nằm bên phải trục Oy.
Khi đó y '  3ax 2  2bx  c  0 có 2 nghiệm phân biệt cùng dương


�
�

 '  b 2  3ac  0
�
�2b
� b  0; c  0 .
Suy ra �  0
3
a
�
�c
0
�
�3a
Câu 25. Chọn đáp án C
Dựa vào đồ thị của f '  x  ta thấy hàm số đồng biến trên khoảng  �;1 và  2; � và nghịch biến
trên khoảng  1;2  . Hàm số đạt cực đại tại x  1 và cực tiểu tại x  2
Khi đó f  1  f  0  và f  1  f  2  suy ra đáp án C sai.
Câu 26. Chọn đáp án C
�
a6
�
�y '  1  3  2a  b  0
2
��
��
Đạo hàm y '  3 x  2ax  b ��
b  9
�y '  3  27  6a  b  0 �
x  1, y  4 ��
� y  1  1  6  9  c  4 � c  0 .
Xét các đáp án ta thấy C sai.

Câu 27. Chọn đáp án D
Quan sát đồ thị ta có:
A sai vì hàm số không nghịch biến trên khoảng  4; �
B sai vì hàm số chỉ đạt cực tiểu tại x  2
C sai vì trên đoạn  1;2 hàm số vừa có khoảng đồng biến, vừa có khoảng nghịch biến
y  max y  2  2  0 .
D đúng vì xmin
� 0;2
x� 1;2
Câu 28. Chọn đáp án A
Đồ thị hàm số y  f  x  không nhận trục hoành làm trục đối xứng.
Câu 29. Chọn đáp án D
Dựa vào bảng biến thiên, ta có các nhận xét sau
 Hàm số đạt cực tiểu tại x  0 và đạt cực đại tại x  2
 Giá trị cực tiểu của hàm số là −1
 Giá trị cực đại của hàm số là 2.
Câu 30. Chọn đáp án B
Gọi hàm số bậc ba có dạng y   x3  ax 2  bx  c , ta có y '  3 x 2  2ax  b; y ''  6 x  2a .
Dựa và bảng biến thiên, ta thấy đồ thị hàm số y  f  x  có hai điểm cực trị là A  1;9  , B  3; 23 .


�
2a  b  3  0
�
�y '  1  0
��
 1 .
 Điểm A  1;9  là điểm cực đại � �
1  a  b  c  9
�

�y  1  9
�
6a  b  27  0
�
�y '  3  0
��
 2 .
 Điểm B  3; 23 là điểm cực tiểu � �
27  9a  3b  c  23
�
�y  3  23
�
�f  2   2
3
2
Từ (1), (2) suy ra a  3, b  9 và c  4 . Vậy f  x    x  3x  9 x  4 � �
.
�f  0   4