ba duong conic hay

Đ
4. Ba đường conic
4. Ba đường conic
Tiết 40: elip
Đường elip là loại đường thường gặp
trong thực tế, ví dụ:
- Bóng của một đường tròn trên mặt đất
bằng phẳng dưới ánh sáng mặt trời là
một đường elip.
- Ta đổ một ít nước màu vào một
cốc thuỷ tinh hình trụ. Nếu ta
nghiêng cốc nước đi thì mặt
thoáng của nước được giới hạn
bởi một đường elip
elip
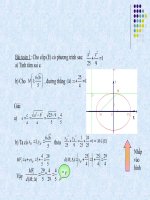
1) Định nghĩa: Cho F
1
, F
2
cố định, F
1
F
2
= 2c.
elip (E) = M(x;y) / F
1
M + F
2
M = 2a ,(0 < c < a)
+ F
1

, F
2
gọi là hai tiêu điểm của elip;
+ Khoảng cách F
1
F
2
= 2c gọi là tiêu cự;
+ e = c/a gọi là tâm sai của elip.
2) Phương trình chính tắc của elip:
M
y
0
Với cách chọn hệ trục toạ độ
như vậy, toạ độ 2 tiêu điểm F
1
, F
2
là bao nhiêu ?
x
F
1
F
2
. .
elip
2) Ph­¬ng tr×nh chÝnh t¾c cña elip:
* F
1
(- c; 0), F

2
(c; 0)
Cho ®iÓm M(x;y) tuú ý,
TÝnh F
1
M
2
, F
2
M
2

?
1) §Þnh nghÜa: Cho F
1
, F
2
cè ®Þnh, F
1
F
2
= 2c.
elip (E) = M(x;y) / F
1
M + F
2
M = 2a ,(0 < c < a)
M
y
0

x
F
1
F
2
. .
elip
2) Ph­¬ng tr×nh chÝnh t¾c cña elip:
* F
1
(- c; 0), F
2
(c; 0)
M(x;y)  F
1
M
2
= (x + c)
2
+ y
2

F
2
M
2
= (x - c)
2
+ y
2

 F
1
M
2
-

F
2
M
2
=
F
1
M
2
+

F
2
M
2
=
4cx
2(x
2
+ c
2
+ y
2
)

Víi mäi ®iÓm M(x,y), xÐt MF
1
F
2
ta lu«n cã:
F
1
M -F
2
M F1F2
 (F
1
M - F
2
M)
2
- 4a
2

= 2c < 2a
 0
1) §Þnh nghÜa: Cho F
1
F
2
= 2c, F
1
, F
2
cè ®Þnh

elip (E) = M(x;y) / F
1
M + F
2
M = 2a ,(0 < c < a)
M
y
0
x
F
1
F
2
. .
eli p (E) = M(x;y) / F
1
M + F
2
M = 2a ,(0 < c < a)
F
1
M
2
-

F
2
M
2
= 4cx ; F

1
M
2
+

F
2
M
2
= 2(x
2
+ c
2
+ y
2
); (F
1
M F–
2
M)
2
4a–
2
 0
M(x;y)  (E) 
F
1
M + F
2
M = 2a 

(F
1
M + F
2
M)
2
- 4a
2
= 0
 (F
1
M + F
2
M)
2
- 4a
2
 (F
1
M - F
2
M)
2
- 4a
2
 = 0
 (F
1
M
2

- F
2
M
2
)
2


- 8a
2
(F
1
M
2
+ F
2
M
2
) + 16a
4
= 0
16 c
2
x
2
 c
2
x
2
– a

2
x
2
- a
2
c
2
- a
2
y
2
+ a
4
= 0
 x
2
(a
2
– c
2
) + a
2
y
2
= a
2
(a
2
– c
2

)
 x
2
b
2
+ a
2
y
2
= a
2
b
2
( víi b
2
= a
2
– c
2
)
2 2
2 2
x y
1
a b
+ =

– 16a
2
(x

2
+ c
2
+ y
2
)
+ 16a
4
= 0

( để ý rằng a > b >0 ).
2 2
2 2
x y
1
a b
+ =
Với b
2
= a
2
c
2
(1)
2) Phương trình chính tắc của elip:
x
F
1
F
2

y
0
M
a) Định lý:

Trong mặt phẳng Oxy, cho 2 điểm
F
1
(-c;0) và F
2
(c;0).
Xét elip (E) = M(x;y) / F
1
M + F
2
M = 2a ,(0 < c < a)
Điều kiện cần và đủ để điểm M(x;y) thuộc (E) là:
b) Định nghĩa: Phương trình (1) được gọi là phương trình
chính tắc của e líp (E)
elip