Ba đường Cônic

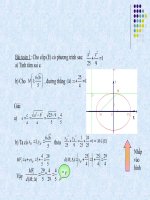
Bài toán 1: Cho elip (E) có phương trình sau:
a) Tính tâm sai e.
b) Cho , đường thẳng , tính tỉ số
2 2
1
25 9
x y
+ =
25
( ) : 0
4
x∆ + =
1
( ; )
MF
d M ∆
6 6
1;
5
M
 
 ÷
 ÷
 
2 2
25 9 4
5 5
c a b
e
a a

− −
= = = =
Giải
a)
1
4 29
5
5 5
M
MF a ex= + = + =
25 25 29
( ; ) 1
4 4 4
M
d M x∆ = + = + =
6 6
1,
5
M M
x y= =
2 2
1 24
1 ( )
25 9 25 25
M M
x y
M E+ = + = ⇒ ∈
b) Ta có thỏa

1

29 4 4
*
( ; ) 5 29 5
MF
d M
= =
∆
Vậy
x
= e

Nhấp
vào
hình

2 2
1
9 16
x y
− =
9
: 0
5
x∆ − =
4
10;
3
M
 
−

 ÷
 
Bài toán 2: Cho Hyperbol (H) có phương trình sau:
a) Tính tâm sai e.
b) Cho , đường thẳng , tính tỉ số
2
( ; )
MF
d M ∆
Giải
a)
2 2
9 16 5
3 3
c a b
e
a a
+ +
= = = =
2
5 5 10 9
3 10
3 3
M
c
MF a x
a
−
= − = − =
9 9 5 10 9

( ; ) 10
5 5 5
M
d M x
−
∆ = − = − =
4
10,
3
M M
x y= = −
b) Ta có thoả

2 2
10 1
1 ( )
9 16 9 9
M M
x y
M H− = − = ⇒ ∈
2
5
( ; ) 3
MF
d M
=
∆
Vậy
= e
Nhấp vào

hình

Nhắc lại định nghĩa
Parabol.
2 2
1
25 9
x y
+ =
25
( ) : 0
4
x∆ + =
Phải chăng đường thẳng là đường chuẩn của elip
( theo như định nghĩa đường chuẩn của Parabol)
2 2
1
9 16
x y
− =
9
: 0
5
x∆ − =
Phải chăng đường thẳng là đường chuẩn của hyperbol
( theo như định nghĩa đường chuẩn của Parabol)

Người soạn: Nguyễn Ngọc Khang
Đối tượng: Lớp 10A1
Ban nâng cao

BA ĐƯỜNG CONIC
Bài toán
Cho elip có phương trình chính tắc:
Đường thẳng:
Với điểm M bất kì thuộc elip, tính tỉ số
1 2
: 0 ; : 0
a a
x x
e e
∆ + = ∆ − =
2 2
2 2
1 ( 0)
x y
a b
a b
+ = > >
1 2
1 2
;
( ; ) ( ; )
MF MF
d M d M∆ ∆