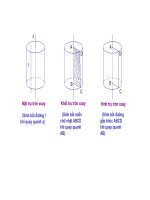
Mat tron xoay

P
O
M
M
C
1. KHÁI NIỆM MẶT TRÒN XOAY
∆
Trong không gian cho một đường thẳng và một
điểm M,
O
O là hình chiếu của M trên .
∆
∆
Đường tròn C
M

được gọi là đường tròn
sinh bởi điểm M khi M
quay quanh
∆


Định nghĩa
Trong mặt phẳng (Q) cho một
đường thẳng và một đường l nào đó.
∆
M
M
l gọi là đường sinh của
mặt tròn xoay (T)

∆
gọi là trục của mặt tròn
xoay (T)
Hình (T) gồm tất cả các
đường tròn C
M
được gọi là
mặt tròn xoay sinh bởi khi quay
quanh
( )
lM
∈
l
∆


∆
l


Ví dụ
ll
∆

2.MẶT TRỤ TRÒN XOAY
∆
Gọi là
Gọi là
trục
trục

của mặt trụ
của mặt trụ


Định nghĩa: Cho hai đường thẳng song song và
cách nhau một khỏang R.
∆
l

Gọi là
Gọi là
đường sinh
đường sinh
của mặt trụ
của mặt trụ
l
R
R
M t tròn xoay sinh ặ
b i đ ng th ng khi quay ở ườ ẳ
quanh g i là ọ
m t tr ặ ụ
m t tr ặ ụ
tròn xoay (M t tr )ặ ụ
tròn xoay (M t tr )ặ ụ
l
∆
l
∆

R
R
Nhận xét
R
R

Nếu cắt mặt trụ bởi một
Nếu cắt mặt trụ bởi một
mp tùy ý vuông góc với thì
mp tùy ý vuông góc với thì
thiết diện nhận được là một
thiết diện nhận được là một
đường tròn
đường tròn
.
.
∆∈
OROC ),,(
∆

{ }
)(),()( constRMdMT
=∆=
∆

Mặt trụ có vô số đường sinh
Mặt trụ có vô số đường sinh


'M

'l