Bài toán dịch chuyển hệ vân giao thoa

TT luyện thi chất lượng cao GV: Nguyễn Tuấn
TRƯỜNG THPT CẦM BÁ THƯỚC BỒI DƯỠNG VẬT LÝ 12
TT ÔN LUYỆN CHẤT LƯỢNG CAO
Giao thoa sóng ánh sáng - Bài toán dịch chuyển hệ vân
Các em thân mến! Phần giao thoa sóng ánh sáng là một phần nói chung không khó lắm trong
chương trình vật lý phổ thông tuy nhiên bài toán dịch chuyển hệ vân giao thoa thì có thể với
nhiều em còn cảm thấy khó giải và hiểu một cách trọn vẹn. Bài viết này sẽ giúp các em làm tốt
dạng bài tập đó.
Phương pháp giải bài toán dịch chuyển hệ vân giao thoa trong giao thoa sóng ánh sáng
Có hai bài toán:
Bài toán 1. Dịch chuyển hệ vân do dịch chuỷen nguồn sáng
Bài toán 2. Dịch chuyển hệ vân do đặt bản mỏng chắn trước một khe sáng.
Bài toán 1
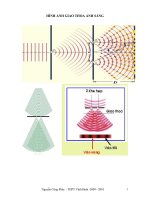
Trong thí nghiệm giao thoa sóng ánh sáng với khe Yang người ta đặt nguồn sáng S trên trung trực
của hai khe S1,S2 cách mặt phắc S1S2 một đoạn (d) tại hai khe S1,S2 sẽ phát ra hai chùm sóng ánh
sáng thoả mãn sóng kết hợp (Cùng tần sô, cùng pha hoặc có độ lệch pha không đổi theo thời gian).
Trên màn quan sát E đặt cách S1S2 một đoạn là D và vuông góc với trung trực của S1,S2 ta quan sát
được một hệ vân giao thoa đối xứng qua vân trung tâm nằm chính giữ tại giao điểm của trung trực
với E(HV1)
Bây giờ nếu dích nguồn S theo phương song song với S1,S2 lên trên(Hoặc xuống dưới) một đoạn là
(Y) thì vân trung tâm sẽ dịch chuyển về phía nào từ đó suy ra sự dịch chuyển của hệ vân?(HV2)
TT luyện thi chất lượng cao GV: Nguyễn Tuấn
Bài giải.
Cơ sở lý luận của dạng toán
Sau khi dịch chuyển S như giả thiết xét sóng tổng hợp tại điểm M bất kỳ trên màn E.
Gọi d1, d2 lần lượt là khoảng cách từ S tới S1, S2. Gọi D1 và D2 lần lượt là khoảng cách từ S1, S2
đến M.
Ta có: Hiệu quang trình của sóng ánh sáng từ S tới M là:
Theo sách giáo khoa vật lý 12NC ta chứng minh được:
Cách chứng minh tương tự cho ta biểu thức liên hệ giữa y, d1, d2, và a,d như sau:
Thay (2) và (3) vào (1) ta được:

Nhận xét:
Điểm M Là điểm sáng thì ta có:
với K là số nguyên (5)
Điểm M Là điểm sáng thì ta có:
với K là số nguyên(6)
Giải quyết vấn đề bài toán đưa ra!
Với vân trung tâm ta có: k = 0 vậy từ (4) và (5) ta có:
suy ra ta được:
dễ thấy tọa độ vân trung tâm là
(6)
Từ (6) suy ra vân trung tâm(Và do đó là hệ vân) dịch chuyển ngược chiều với chiều dịch chuyển của
nguồn S. Và dịch đi một đoạn đúng bằng :
Mở rộng bài toán
Ngoài bài toán này ra ta còn có một số bài toán liên quan như:
Xác định vị trí vân sáng thứ bậc n hay vân tối bậc n sau khi đã dịch chuyển S.
Nếu là tìm vị trí vân sáng:
Từ (4) và (5) ta tìm được biểu thức xác định Xs. Chú ý vân sáng bậc n ứng với K = |n|
Nếu tìm vị trí vân tối:
Từ (4) và (6) ta tìm được biểu thức xác định Xt. Chú ý:
Ở phần dương(K>0) vân tối thứ n ứng với K = n+1
Ở phần âm(K<0) vân tối thứ n ứng với K = n
Câu hỏi sáng tạo:
Hệ vân dịch chuyển vậy khoảng vân i biến đổi thế nào?

TT luyện thi chất lượng cao GV: Nguyễn Tuấn
Bài toán 2
Thí nghiệm Young có bản mặt mỏng song song được làm bởi chất có chiết suất n và độ dày e:
Do phải đi qua bản mỏng nên quang lộ từ S1 đến M sẽ thay đổi:
Quang lộ từ S2 đến M không đổi:
Hiệu quang hình:

Vị trí vân sáng:
Hệ văn dịch chuyển một đoạn về phía có đặt bản mặt song song: