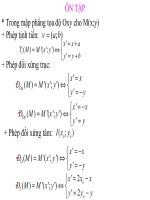tai lieu on tap chuong 1 hinh hoc 11

Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng

CHƯƠNG I

PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG
MẶT PHẲNG
 Bài 1. Phép biến hình
 Kiến thức cơ bản
Định nghĩa: Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất

M ′ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
Nếu kí hiệu phép biến hình là F thì ta viết F ( M ) = M ′ và gọi M ′ là ảnh của điểm M qua phép
biến hình F
Phép biến hình biến mỗi điểm M của mặt phẳng thành chính nó được gọi là phép đồng nhất.

 Bài 2. Phép tịnh tiến
 Kiến thức cơ bản
1. Định nghĩa
Trong mặt phẳng cho vectơ

v

. Phép biến hình biến mỗi điểm M thành điểm M ′ sao

cho ................. được gọi là phép tịnh tiến theo vectơ

v

. Kí hiệu là

T

v

,(

v

được gọi là

vectơ tịnh tiến ).
Như vậy: Tv ( M ) = M ′ ⇔     
Phép tịnh tiến theo vectơ – khơng là ................................................
2. Tính chất
Tính chất 1: Nếu Tv ( M ) = M ′, Tv ( N ) = N ′ thì ........................ và từ đó suy ra.........................
Ta cịn nói phép tịnh tiến ......................... khoảng cách giữa hai điểm bất kì.
Tính chất 2: Phép tịnh tiến
• Biến đường thẳng thành...........................................................................................................
• Biến đoạn thẳng thành .............................................................................................................
• Biến tam giác thành .................................................................................................................
• Biến đường trịn thành .............................................................................................................
3. Biểu thức tọa độ

Biên soạn: Tăng Văn Thi

Trang 1


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
Trong mặt phẳng Oxy cho điểm

M ( x; y ), v =(a; b ) .

Gọi điểm M ′( x′; y′) = Tv ( M ) . Khi đó ta

có biểu thức tọa độ:....................................................................................................................
Ví dụ 1. Cho hình bình hành ABCD. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo
vectơ AD .
Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho điểm A(3;5) và

v =( − ;2 )
1

và đường thẳng d có

phương trình 2 x − 3 y + 5 = 0 . Tìm ảnh của điểm A và đường thẳng d qua phép tịnh tiến theo
vectơ

v

.

Ví dụ 3. Trong mặt phẳng tọa độ Oxy cho đường trịn (C) có phương trình
x 2 + y 2 − 4 x + 6 y −12 = 0 .

Tìm ảnh của (C) qua phép tịnh tiến theo vectơ

v =( −2;3)

 Bài tập thực hành
1. Trong mặt phẳng tọa độ Oxy cho

v =(2;− ) ,
1

điểm A( −3;5) . Tìm tạo độ các điểm B sao

cho:
a. Tv ( A) = B

b.

2. Trong mặt phẳng tọa độ Oxy cho
2 x − 3 y + 3 = 0 , đường thẳng d1

Tv ( B ) = A

v =( −2;1) ,

đường thẳng d có phương trình

có phương trình 2 x − 3 y − 5 = 0 .

a. Viết phương trình của đường thẳng d ′ là ảnh của d qua Tv .
b. Tìm tọa độ của

w

có giá vng góc với đường thẳng d để d1 là ảnh của d qua Tw

3. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3 x − y − 9 = 0 . Tìm phép tịnh

tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d ′ đi qua gốc
tọa độ và viết phương trình đường thẳng d ′ .
4. Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình
Tìm ảnh của (C) qua phép tịnh tiến theo vectơ

x2 + y 2 − 2x + 4 y − 4 = 0 .

v =(1;− )
3

5. Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến
theo vectơ AG . Xác định điểm D sao cho phép tịnh tiến theo vectơ AG biến điểm D thành
điểm A.

 Bài 3. Phép đối xứng trục
 Kiến thức cơ bản
1. Định nghĩa
Cho đường thẳng d . Phép biến hình biến mỗi điểm M thuộc d thành ........................, biến
mỗi điểm M không thuộc d thành M’ sao cho d là ............................................. của đoạn
Biên soạn: Tăng Văn Thi

Trang 2


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
thẳng MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d . Kí
hiệu Đd ( đường thẳng d được gọi là trục đối xứng )
Vậy: Đd ( M ) = M ′ ⇔  , trong đó M0 là hình chiếu vng góc của M lên đường
thẳng d .
2. Biểu thức tọa độ

Trong mặt phẳng tọa độ Oxy , với mỗi điểm M ( x; y ) , gọi M ′( x′; y ′ ) = Đd ( M )

 Nếu chọn d

 x′ = .........
là trục Ox thì ta có: 
 y′ = .........

 Nếu chọn d là trục Oy thì ta có:

 x′ = .........

 y′ = .........

3. Tính chất của phép đối xứng trục
Phép đối xứng trục
 .............................khoảng cách giữa hai điểm bất kì
 Biến đường thẳng thành..........................................................................................................
 Biến đoạn thẳng thành ...........................................................................................................
 Biến tam giác thành ...............................................................................................................
 Biến đường tròn thành ...........................................................................................................
4. Trục đối xứng của một hình
Đường thẳng d được gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến H
thành chính nó. Khi đó ta nói H là hình có trục đối xứng.
Ví dụ: Trong mặt phẳng tọa độ Oxy , cho điểm M (1;5) , đường thẳng d có phương trình
x −2y + 4 = 0

và đường trịn (C) có phương trình

x2 + y 2 − 2x + 4 y − 4 = 0

a. Tìm ảnh của M , d và (C) qua phép đối xứng trục Ox
b. Tìm ảnh của M qua phép đối xứng qua đường thẳng d

 Bài tập thực hành
5
1. Trong mặt phẳng tọa độ Oxy , cho điểm M ( 3;− ) , đường thẳng d có phương trình
3x + 2 y − 6 = 0

và đường trịn (C) có phương trình

Biên soạn: Tăng Văn Thi

Trang 3

x2 + y2 + 4x − 6 y − 3 = 0 .


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
a. Tìm ảnh của M , d và (C) qua phép đối xứng trục Ox
b. Tìm ảnh của M , d và (C) qua phép đối xứng trục Oy
2. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x − 5 y + 7 = 0 và đường

thẳng d ′ có phương trình 5 x − y −13 = 0 . Tìm phép đối xứng biến d thành d ′ .

 Bài 4. Phép đối xứng tâm
 Kiến thức cơ bản
1. Định nghĩa
Cho điểm I. Phép biến hình biến mỗi điểm I thành ........................, biến mỗi điểm M khác I
thành M’ sao cho I là ............................. của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.

Kí hiệu ĐI ( I là tâm đối xứng )
Vậy ĐI ( M ) = M ′ ⇔ 
2. Biếu thức tọa độ
Trong mặt phẳng tọa độ Oxy cho M ( x; y ), M ′( x ′; y ′) .
 Nếu ĐO ( M ) = M ′ , O là gốc tọa độ thì ta có:

 x′ = .........

 y′ = .........

 x′ = .........
 Nếu Đ ( M ) = M ′ , I ( a; b ) thì ta có: 
 y′ = .........
I

3. Tính chất
Tính chất 1: Nếu ĐI ( M ) = M ′, ĐI ( N ) = N ′ thì ........................ và từ đó suy ra.........................
Ta cịn nói phép đối xứng tâm ......................... khoảng cách giữa hai điểm bất kì.
Tính chất 2:
Phép đối xứng tâm
 Biến đường thẳng thành..........................................................................................................
 Biến đoạn thẳng thành ...........................................................................................................
 Biến tam giác thành ...............................................................................................................
 Biến đường tròn thành ...........................................................................................................
4. Tâm đối xứng của một hình

Biên soạn: Tăng Văn Thi

Trang 4

Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến H thành chính nó.
Ví dụ 1. Các hình có tâm đối xứng là.......................................................................................
Ví dụ 2. Trong mặt phẳng tọa độ Oxy , cho điểm M (1;5) , đường thẳng d có phương trình
x −2y + 4 = 0

và đường trịn (C) có phương trình

x2 + y 2 − 2x + 4 y − 4 = 0 .

Tìm ảnh của

M , d , ( C ) qua phép đối xứng tâm O.

 Bài tập thực hành
5
1. Trong mặt phẳng tọa độ Oxy , cho điểm M (3;− ) , đường thẳng d có phương trình
3x + 2 y − 6 = 0

và đường trịn (C) có phương trình

x2 + y2 + 4x − 6 y − 3 = 0 .

Tìm ảnh của

M , d , ( C ) qua phép đối xứng tâm O.

2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng

d : x −2y +2 = 0

và d ′ : x − 2 y − 8 = 0 . Tìm

phép đối xứng tâm biến d thành d ′ và biến trục Ox thành chính nó.
3. Trong mặt phẳng tọa độ Oxy , cho hai điểm M ( −2;3), I (1;2 ) , đường thẳng d có phương
trình 3 x − y + 9 = 0 và đường tròn (C) có phương trình

x 2 + y 2 + 2x − 6 y + 6 = 0 .

a. Tìm ảnh của M , d , ( C ) qua phép đối xứng tâm O.
b. Tìm ảnh của M , d , ( C ) qua phép đối xứng tâm I.

 Bài 5. Phép quay
 Kiến thức cơ bản
1. Định nghĩa
Cho điểm O và góc lượng giác α . Phép biến hình biến O thành chính nó, biến mỗi điểm M
khác O thành điểm M ′ sao cho ...................... và góc lượng giác ( OM ; OM ′) = ........ được
gọi là phép quay tâm O góc α . Kí hiệu Q( O ,α ) ( O là tâm quay, α là góc quay )

      
Vậy Q ( M ) = M ′ ⇔ 
( O;α )
      
Nhận xét:
 Quy ước: chiều dương của đường tròn lượng giác là chiều ngược chiều quay của kim đồng
hồ.
 Với k là số nguyên ta ln có:
• Phép quay Q( O , 2 kπ ) là .....................................

Biên soạn: Tăng Văn Thi

Trang 5


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
• Phép quay Q( O , ( 2 k +1) π ) là ..........................................

Ví dụ 1. Cho lục giác đều ABCDEF tâm O. Tìm ảnh của ∆ABC qua phép quay tâm O một
góc

60 0 ,120 0 ,− 0
60

2. Tính chất
Phép quay
 .............................khoảng cách giữa hai điểm bất kì
 Biến đường thẳng thành..........................................................................................................
 Biến đoạn thẳng thành ...........................................................................................................
 Biến tam giác thành ...............................................................................................................
 Biến đường tròn thành ...........................................................................................................
Chú ý:
π
 Q( O ,α ) ( d ) → d ′ thì ( d, d ′ ) = α nếu 0 < α ≤

2

π
 Q( O ,α ) ( d ) → d ′ thì ( d, d ′ ) = π − α nếu < α < π
2

3. Biểu thức tọa độ của phép quay đặc biệt
Trong mặt phẳng tọa độ Oxy cho M ( x; y ), M ′( x′; y′)



M ′( x′; y′) = Q



M ′( x′; y ′) = Q

0
 O , 90 




( M ) khi đó ta có biểu thức tọa độ:

0
 O , −90 




 x′ = − y

 y′ = x

( M ) khi đó ta có biểu thức tọa độ:

 x′ = y

 y′ = − x

Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho điểm A(3;5) , B ( − 2;7 )
a. Tìm ảnh của A, B qua phép quay tâm O một góc 90 0
b. Tìm ảnh của A, B qua phép quay tâm O một góc − 90 0

 Bài tập thực hành
1. Cho hình vng ABCD tâm O. M là trụng điểm của AB, N là trung điểm của OA. Tìm ảnh
của tam giác AMN qua phép quay tâm O góc 900.
2. Cho hình lục giác đều ABCDEF , O là tâm đối xứng của nó, I là trung điểm của AB.

a. Tìm ảnh của tam giác AIF qua phép quay tâm O góc 1200.
Biên soạn: Tăng Văn Thi

Trang 6


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
b. Tìm ảnh của tam giác AOF qua phép quay tâm E góc 600.
3. Trong mặt phẳng tọa độ Oxy cho điểm A(3;4 ) . Hãy tìm tọa độ điểm A′ là ảnh của A

qua phép quay tâm O góc 900.
4. Trong mặt phẳng tọa độ Oxy cho các điểm A(3;3), B ( 0;5), C (1;1) và đường thẳng d có

phương trình 5 x − 3 y + 15 = 0 . Hãy xác định tạo độ các đỉnh của tam giác A′B′C ′ và
phương trình đường thẳng d ′ theo thứ tự là ảnh của tam giác ABC và đường thẳng d

qua phép quay tâm O, góc quay 900.

 Bài 6. Khái niệm phép dời hình và hai hình bằng nhau
 Kiến thức cơ bản
1. Khái niệm phép dời hình
Định nghĩa: Phép dời hình là phép biến hình.......................... khoảng cách giữa hai điểm bất kì.
Nhận xét:
 Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những
phép dời hình.
 Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép
dời hình.
2. Tính chất
Phép dời hình
 Biến ba điểm thẳng hàng thành...............................................................................................
.....................................................................................................................................................
 Biến đường thẳng thành.................................., biến tia thành...............................................
 Biến đoạn thẳng thành ..........................................................................................................
 Biến tam giác thành ..............................................................................................................
 Biến góc thành.......................................................................................................................
 Biến đường trịn thành ..........................................................................................................
Chú ý: ( SGK )
Ví dụ 1. Cho lục giác đều ABCDEF, O là tâm đường tròn ngoại tiếp của nó. Tìm ảnh của tam
giác OAF qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng trục EB và
phép quay tâm O góc -600.
Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho A( −1;3), B ( 2;5) .

Biên soạn: Tăng Văn Thi

Trang 7

Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
a. Tìm ảnh A′ của A qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối

xứng trục Ox và phép tịnh tiến theo vectơ

v =(3;2 )

b. Tìm ảnh B ′ của B qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay
3
tâm O góc 900 và phép đối xứng tâm I ( 4;− )

Ví dụ 3. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 3x − y − 3 = 0 .
Viết phương trình đường thẳng d ′ là ảnh của d qua phép dời hình có được bằng cách thực
hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ

v =( −2;1) .

3. Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia
Ví dụ. ( SGK )

 Bài tập thực hành
1. Trong mặt phẳng tọa độ Oxy , cho

v =(3;− )
1

và điểm M ( − 2;4 )

a. Tìm tọa độ của điểm M ′ là ảnh của M qua phép dời hình có được bằng cách thực hiện

liên tiếp phép đối xứng qua trục Ox và phép tịnh tiến theo vectơ

v

b. Tìm toa độ của điểm M ′′ là ảnh của M qua phép dời hình có được bằng cách thực hiện

liên tiếp phép tịnh tiến theo vectơ

v

và phép đối xứng qua trục Oy

2. Trong mặt phẳng tọa độ Oxy , cho
2x − y = 0 .

v =(3;1)

và đường thẳng d có phương trình

Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép

quay tâm O góc 90 0 và phép tịnh tiến theo vectơ

v

.

 Bài 7. Phép vị tự

 Kiến thức cơ bản
1. Định nghĩa
Cho điểm O và số k ≠ 0 . Phép phép biến hình biến mỗi điểm M thành điểm M ′ sao
cho ........................... được gọi là phép vị tự tâm O, tỉ số k. Kí hiệu V( O ,k ) ( O là tâm vị tự )
Như vậy, V( O,k ) ( M ) = M ′ ⇔ 
Nhận xét:
 Phép vị tự biến tâm vị tự thành chính nó
 Khi k =1 , phép vị tự là..........................................................................................................
 Khi k = −1 , phép vị tự là.......................................................................................................
 V( O,k ) ( M ) = M ′ ⇔ 
Biên soạn: Tăng Văn Thi

Trang 8


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
2. Tính chất
Tính chất 1: Nếu V( O ,k ) ( M ) = M ′,V( O ,k ) ( N ) = N ′ thì ........................ và ...................................
Tính chất 2:
Phép vị tự tỉ số k
 Biến ba điểm thẳng hàng thành.............................................................................................
.....................................................................................................................................................
 Biến đường thẳng thành......................................................................................., biến tia
thành tia, biến đoạn thẳng thành đoạn thẳng.
 Biến tam giác thành ............................................................,biến góc thành..........................
 Biến đường trịn thành ..........................................................................................................
3. Tâm vị tự của hai đường trịn
Định lí: Với hai đường trịn bất kì ln có một phép vị tự biến đường trịn này thành đường
trịn kia.
Cách tìm tâm vị tự của hai đường trịn ( SGK ).

4
Ví dụ 1. Trong mặt phẳng tọa độ Oxy , cho điểm A(1;3), B ( 2;− ) .

a. Tìm ảnh của A qua V( B ,−2 )
b. Tìm tọa độ tâm I sao cho V( I ,3 ) ( A) = B

Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho hai điểm A( 2;1), B (8;4 ) . Tìm phép vị tự biến
đường tròn ( A;2 ) thành đường tròn ( B;4 )

 Bài tập thực hành
1. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 3x + 2 y − 6 = 0 . Hãy

viết phương trình của đường thẳng d ′ là ảnh của d phép vị tự tâm O tỉ số k = −2 .
2. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 2 x + y − 4 = 0 .
a. Hãy viết phương trình của đường thẳng d1 là ảnh của d phép vị tự tâm O tỉ số k = 3 .
b. Hãy viết phương trình của đường thẳng d 2 là ảnh của d phép vị tự tâm I ( −1;2 ) tỉ số
k = −2 .

3. Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình ( x − 3) 2 + ( y + 1) 2 = 9 . Hãy
viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I (1;2 ) tỉ số k = −2

 Bài 8. Phép đồng dạng
 Kiến thức cơ bản
Biên soạn: Tăng Văn Thi

Trang 9


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
1. Định nghĩa

Phép biến hình F được gọi là phép đồng dạng tỉ số k ( k > 0) , nếu với hai điểm M , N bất kì
và ảnh M ′, N ′ tương ứng của chúng ta ln có ...........................................
Nhận xét:
• Phép dời hình là ...................................... tỉ số ......
• Phép vị tự tỉ số k là ....................................... tỉ số .....
• Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được

phép đồng dạng tỉ số .......
2. Tính chất
Phép đồng dạng tỉ số k :
 Biến ba điểm thẳng hàng thành.............................................................................................
.....................................................................................................................................................
 Biến đường thẳng thành......................................................................................., biến tia
thành tia, biến đoạn thẳng thành đoạn thẳng.
 Biến tam giác thành ............................................................,biến góc thành..........................
 Biến đường trịn thành ..........................................................................................................
Ví dụ 1. Trong mặt phẳng tọa độ Oxy , cho điểm M ( 2;4 ) . Tìm ảnh của M qua phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k =

1
2

và phép đối xứng qua

trục Oy.
Ví dụ 2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình 2 x − y = 0 . Tìm
ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (1;2 )
tỉ số k = −2 và phép đối xứng qua trục Ox.
Ví dụ 3. Trong mặt phẳng tọa độ Oxy , cho đường trịn (C) có phương trình

( x − 2) 2 + ( y − 4) 2 = 4 . Tìm ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên
tiếp phép vị tự tâm O tỉ số k =

1
2

và phép quay tâm O góc -900.

3. Hai hình đồng dạng
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình
kia.

 Bài tập thực hành
Biên soạn: Tăng Văn Thi

Trang 10


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
1. Trong mặt phẳng tọa độ Oxy , cho điểm A( −3;4 ) . Tìm ảnh của A qua phép đồng dạng có
1
được bằng cách thực hiện liên tiếp phép vị tự tâm I (1;2 ) tỉ số k = − và phép đối xứng
2

qua trục Ox.
2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình 2 x − y + 3 = 0 . Tìm ảnh

của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
v =(2;3)

và phép vị tự tâm I ( −1;4 ) tỉ số k = 2 .

3. Trong mặt phẳng tọa độ Oxy , cho đường trịn (C) có phương trình ( x −1) 2 + ( y + 2) 2 = 4 . Tìm
ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (3;5)
tỉ số k = −3 và phép đối xứng tâm O.

BÀI TẬP TRẮC NGHIỆM CHƯƠNG I
Câu 1: Trong mp Oxy cho đường thẳng d có pt 3x-2y-1=0. Ảnh của đt d qua phép đối xứng tâm
O có pt là:
a. .3x + 2y + 1=0

b. -3x + 2y - 1=0

c. 3x + 2y - 1=0

d. 3x - 2y - 1=0
r

r

Câu 2: Trong mp Oxy cho v = (2; −1) và điểm (-3;2). Ảnh của điểm M qua phép tịnh tiến v là:
a. (1;-1)

b.(-1;1)

c.(5;3)

d.(1;1)

Câu 3: Trong mp Oxy cho đường thẳng d có pt 2x + 3y – 3 = 0. Ảnh của đt d qua phép vị tự tâm

O tỉ số k = 2 biến đường thẳng d thành đường thẳng có pt là:
a. 2x + y – 6 = 0

b. 4x + 2y – 5 = 0

c. 2x + y + 3 = 0

d .4x - 2y – 3 = 0

Câu 4: Trong mp Oxy, cho điểm M ( 2 ; 4). Hỏi phép đồng dạng có được bằng cách thực hiện
liên tiếp phép vị tự tâm O tỉ số k =

1
2

và phép đối xứng trục Oy sẽ biến điểm M thành điểm nào

sau đây?
a.(-2;4)

b.(-1;2)

c.(1;2)

d.(1;-2)

Câu 5: Trong mp Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O,
góc 450:
Biên soạn: Tăng Văn Thi

Trang 11


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
a. (0; 2)

b.(-1;1)

c.(1;0)

d.( 2 ;0)

Câu 6: Có bao nhiêu phép tịnh tiến biến hình vng thành chính nó:
a. 0

b. 1

c. 2

d. 3

Câu 7:Có bao nhiêu phép quay tâm O góc α , 0 ≤ α ≤ 2π , biến tam giác đều tâm O thành chính nó
a. 4

b.1

c. 2

d. 3

Câu 8: Trong mp Oxy choM(-2;4). Ảnh của điểm M qua phép vị tự tâm O tỉ số k = -2 là:
a.(4;8)

b.(-8;4)

c.(4;-8)

d.(-4;-8)

Câu 9: Trong các phép biến hình sau, phép nào khơng phải là phép dời hình
a. Phép chiếu vng góc lên một đường thẳng
b. Phép đối xứng trục
c. Phép đồng nhất
d. Phép vị tự tỉ số -1
Câu 10: Trong các hình sau, hình nào có vơ số tâm đối xứng ?
a .Đường elip

b. Hai đường thẳng song song

c. Hình lục giác đều

d. Hai đường thẳng cắt nhau

r
r
Câu 11: Trong mp Oxy cho v = (1; 2) và điểm (2;5). Ảnh của điểm M qua phép tịnh tiến v là:

a. (1;6)

b.(3;1)

c.(3;7)

d.(4;7)

Câu 12: Trong mp Oxy cho điểm M (2;3). Hỏi M là ảnh của điểm nào sau đây qua phép đối xứng
trục Ox:
a. (3;-2)

b.(2;-3)

c.(-2;3)

d.(3;2)

Câu 13: Trong mp Oxy, cho đường thẳng d:2x – y = 0. Hỏi phép đồng dạng có được bằng cách
thực hiện liên tiếp phép vị tự tâm O tỉ số k = - 2 và phép đối xứng trục Oy sẽ biến đường thẳng d
thành đường thẳng nào sau đây:
a. 2x + y - 2=0

c. 2x + y = 0

c. 2x – y = 0

d. 4x – y = 0

Câu 14: Trong mp Oxy cho đường trịn (C) có pt ( x − 1) 2 + ( y − 2) 2 = 4 . Hỏi phép vị tự tâm O tỉ số
k = - 2 biến (C) thành đường tròn nào sau đây:
a. ( x − 4) 2 + ( y − 2) 2 = 4

b. ( x − 4) 2 + ( y − 2) 2 = 16

c. ( x + 2) 2 + ( y + 4) 2 = 16

d. ( x − 2) 2 + ( y − 4) 2 = 16

Biên soạn: Tăng Văn Thi

Trang 12


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
r

Câu 15: Trong mp Oxy cho đường thẳng d có pt 2x – y + 1 = 0. Để phép tịnh tiến theo v biến đt
r

d thành chính nó thì v phải là vectơ nào sau đây:
a.

v =(2;1)

b.

v =(1;2 )

c.

v =( − ;2 )
1

d.

v =( 2;− )
1

Câu 16: Hình gồm hai đường trịn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng:
a. 0

b.1

c. 2

d. vơ số

Câu 17: Hình gồm hai đường trịn có cùng bán kính có bao nhiêu tâm đối xứng:
a. 0

b.1

c.2

d.vơ số

Câu 18: Trong mp Oxy cho đường thẳng d có phương trình 3x-2y+1=0. Ảnh của đt d qua phép
đối xứng trục Oy có pt là:
a. 3x + 2y + 1 = 0

b. -3x + 2y – 1 = 0

c. 3x + 2y – 1 = 0

d. 3x - 2y + 1 = 0

Câu 19: Trong mp Oxy, cho điểm M(2;1). Hỏi dời hìnhcó được bằng cách thực hiện liên tiếp
r

phép đối xứng tâm O và phép tịnh tiến v = (2;3) sẽ biến điểm M thành điểm nào sau đây:
a. (2;0)

b. (4;4)

c. (1;3)

d. (0;2)

r
Câu 20: Trong mp Oxy cho v = (2;1) và điểm A(4;5). Hỏi A là ảnh của điểm nào trong các điểm
r
sau đây qua phép tịnh tiến v :

a. (1;6)

b. (2;4)

c. (4;7)

d. (3;1)

Câu 21: Trong các mệnh đề sau , mệnh đề nào sai:

a. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
b. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
c. Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
d. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Câu 22: Trong mp Oxy cho điểm M(2;3). Điểm nào sau đây là ảnh của M qua phép đối xứng qua
đường thẳng x – y = 0:
a. ( 3; 2)

b.(-2;3)

c.(2;-3)

Câu 23: Trong các mệnh đề sau , mệnh đề nào sai:
a. Hai đường thẳng bất kì ln đồng dạng
b. Hai hình vng bất kì ln đồng dạng
c. Hai hình chữ nhật bất kì luôn đồng dạng
Biên soạn: Tăng Văn Thi

Trang 13

d.(3;-2)


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
d. Hai đường trịn bất kì ln đồng dạng
Câu 24: Có bao nhiêu phép tịnh tiến biến một đường trịn cho trước thành chính nó:
a. 0

b. 1

c. 2

d. vơ số

c. 2

d. vơ số

Câu 25: Hình vng có mấy trục đối xứng:
a. 4

b. 1

Câu 26: Trong các mệnh đề sau , mệnh đề nào sai:
a. Có một phép vị tự biến mọi điểm thành chính nó
b. Có một phép đối xứng trục biến mọi điểm thành chính nó.
c. Có một phép tịnh tiến biến mọi điểm thành chính nó.
d. Có một phép quay biến mọi điểm thành chính nó.
Câu 27: Trong mp Oxy cho đường thẳng d: x – y + 4=0. Hỏi trong 4 đường thẳng cho bởi các pt
sau đt nào có thể biến thành d qua phép đối xứng tâm
a. 2x + y – 4 = 0

b. 2x + 2y – 3 = 0

c. x + y – 1 = 0

d. 2x - 2y + 1 = 0

Câu 28: Trong mp cho đường tròn (C): ( x − 1) 2 + ( y + 2) 2 = 4 . Hỏi phép dời hình có được bằng
r

cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến v = (2;3) biến (C) thành
đường tròn nào trong các đường tròn sau
a. ( x −1) 2 + ( y −1) 2 = 4

b. ( x − 2) 2 + ( y − 3) 2 = 4

c. ( x − 2) 2 + ( y − 6) 2 = 4

d.

x2 + y2 = 4

Câu 29: trong các mệnh đề sau, mệnh đề nào đúng:
a. Một hình có vơ số trục đối xứng thì hình đó phải là đường trịn
b. Một hình có vơ số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vng góc
c. Đường trịn là hình có vơ số trục đối xứng.
d. Một hình có vơ số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm
Câu 30: trong các mệnh đề sau, mệnh đề nào đúng:
a. Có một phép đối xứng trục biến mọi điểm thành chính nó
b. Có một phép tịnh tiến theo vecto khác khơng biến mọi điểm thành chính nó
c. Có một phép quay biến mọi điểm thành chính nó
d. Có một phép đối xứng tâm biến mọi điểm thành chính nó

Biên soạn: Tăng Văn Thi

Trang 14


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng

Câu 31: Trong mp Oxy cho đường thẳng d: x + y – 2 = 0. Hỏi phép vị tự tâm O tỉ số k = -2 biến d
thành đt nào trong các đt sau:
a. 2x + 2y – 4 = 0

b. x + y + 4 = 0

c. x + y – 4 = 0

d. 2x + 2y = 0

Câu 32: Trong các mệnh đề sau, mệnh đề nào đúng:
a. Phép đối xứng tâm khơng có điểm nào biến thành chính nó
b. Có phép đối xứng tâm có hai điểm biến thành chính nó
c. Có phép đối xứng tâm có vơ số điềm biến thành chính nó.
d. Phép đối xứng tâm có đúng một điểm biến thành chính nó.
Câu 33: có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó
a. 0

b.1

c. 2

d.v ô số

Câu 34: trong các mệnh đề sau, mệnh đề nào đúng:
a. Thực hiện liên tiếp 2 phép tịnh tiến sẽ được 1 phép tịnh tiến
b. Thực hiện liên tiếp phép đối xứng qua tâm và phép đối xứng trục sẽ được một phép đối
xứng qua tâm
c. Thực hiện liên tiếp phép quay và phép tịnh tiến sẽ được phép tịnh tiến.
d. Thực hiện liên tiếp hai phép đối xứng trục sẽ được một phép đối xứng trục

Câu 35: Trong mp Oxy cho đường thẳng d:x = 2. Trong 4 đt sau đt nào là ảnh của d qua phép đối
xứng tâm O
a. y = 2

b. x = -2

c .x = 2

d. y = -2

Câu 36: Cho hình vng tâm O, có bao nhiêu phép quay tâm O góc α , 0 ≤ α ≤ 2π , biến hình
vng thành chính nó:
a.1

b. 3

c. 2

d. 4

Câu 37: Trong mp Oxy cho M(2;3), điểm nào sau đây là ảnh của M qua phép đối xứng trục Ox:
a. (2;-3)

b. (3;2)

c. (-2;3)

d. (3;-2)

Câu 38: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc quay k 2π , k là số

ngun
a. 1

b. 0

c. 2

d. vơ số

Câu 39: Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc quay
α , 0 ≤ α ≤ 2π biến hình chữ nhật thành chính nó

a. 0
Biên soạn: Tăng Văn Thi

b. 3

c. 2
Trang 15

d. 4


Chương I – Phép dời hình và phép đồng dạng trong mặt phẳng
Câu 40: Trong mp Oxy, cho đường tròn (C) ( x − 2) 2 + ( y − 2)2 = 4 . Hỏi phép đồng dạng có được
bằng cách thực hiện liên tiếp phép vị tự tâm O, tỉ số k = 1/2 và phép quay tâm O góc 90 o biến (C)
thành đường trịn nào sau đây:
a. ( x + 2 ) 2 + ( y −1) 2 = 1

b. ( x − 2 ) 2 + ( y − 2) 2 = 1

c. ( x +1) 2 + ( y −1) 2 = 1

d. ( x −1) 2 + ( y −1) 2 = 1

Biên soạn: Tăng Văn Thi

Trang 16