VTTĐ giua mat cau va mp

TRƯỜNG THPT NGUYỄN TRÃI NINH HÒA

XIN TON TRONG BAN QUYEN –
DUNG THAY TEN DOI HO – VI BAI
GIANG NAY TOI DA TANG CHO
TAT CA DONG NGHIEP CUA TOI
VA DA GIANG THU TAI RAT
NHIEU NOI





MÆT CÇU
MÆT CÇU
* VỊ TRÍ TƯƠNG ĐỐI GIỮA MẶT CẦU VÀ MẶT PHẲNG.
* MẶT CẦU NGOẠI TIẾP HÌNH ĐA DIỆN.
* ĐIỀU KIỆN ĐỂ HÌNH CHÓP NGOẠI TIẾP MẶT CẦU
* KIỂM TRA BÀI CŨ
* CỦNG CỐ BÀI VÀ DẶN DÒ

1) Tìm điều kiện để một điểm M nằm ngoài, nằm trong,
hay thuộc mặt cầu S(O,R).
2) Cho mặt cầu S(O,R) và mặt phẳng (P) có khoảng
cách đến O bằng d >R. Lấy điểm M tuỳ ý trên (P). Hãy
xét vị trí của M đối với (S).
Tìm tất cả các điểm chung của (S) và (P).

1) Cho S(O,R).
M thuộc (S) <-> OM = R

M nằm ngoài (S) <-> OM >R
M nằm trong (S) <-> OM <R
1) Tìm điều kiện để một điểm M nằm ngoài, nằm trong,
hay thuộc mặt cầu S(O,R).

2) Cho mặt cầu S(O,R) và mặt phẳng (P) có khoảng cách
đến O bằng d >R. Lấy điểm M tuỳ ý trên (P). Hãy xét vị trí
của M đối với (S).
Tìm tất cả các điểm chung của (S) và (P).
Dựng OH (P) tại H.
Khoảng cách từ O đến (P)
bằng OH = d.
⊥
.H
.M
.O
Khoảng cách từ O đến mp
(P) xác định cách nào ?
D
ự
n
g
O
H


(
P
)
t

ạ
i
H
.
K
h
o
ả
n
g
c
á
c
h
t
ừ

O

đ
ế
n
(
P
)
b
ằ
n
g
O

H

=

d
⊥
Dựng OH (P) tại H.
Khoảng cách từ O đến (P)
bằng OH = d.
OM >= OH = d > R. Vậy
OM > R; suy ra M nằm
ngoài mặt cầu (S).
⊥
Dựng OH (P) tại H. Khoảng
cách từ O đến (P) bằng OH =
d.
OM >= OH = d > R. Vậy OM >
R; suy ra M nằm ngoài mặt
cầu (S).
Mọi điểm M thuộc (P) luôn
nằm ngoài (S) nên (P) và (S)
không có điểm chung.
⊥
Từ câu 2) (S) và (P) không có điểm
chung (nếu (P) ở xa (S).) Nếu đưa
(P) đến gần (S), phải chăng chúng
có thể có điểm chung? Bài học mới
sẽ giải quyết vấn đề này.
Bạn hãy giải thích vì sao OM>=OH
Do khoảng cách từ điểm O đến một

mp thì ngắn hơn hoặc bằng khoảng
cách từ O đến một điểm bất kỳ thuộc
mp đó.
quan sat

.O
.H
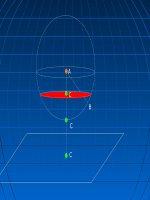
Cho mặt cầu S(O,R) và mp(P). Khoảng cách từ O đến (P)
bằng d. Gọi H là hình chiếu của O trên (P): OH = d
Giữa d và R có các khả
năng nào xảy ra?
Ta xét sự tương giao của
mp(P) và mặt cầu (S)
trong mỗi trường hợp đó
d > R
(P) và (S) không có điểm chung.
Nói: (P) và (S) không cắt nhau
Trường hợp d > R ; kết luận gì
về sự tương giao của (P) và
(S)?
Xét các trường hợp:
d > R, d = R, d < R

Vậy kết luận gì về sự
tương giao của (S) và
(P) ?
.O
.H
Cho mặt cầu S(O,R) và mp(P). Khoảng cách từ O đến (P)
bằng d. Gọi H là hình chiếu của O trên (P): OH = d

2. Vị trí tương đối giữa mặt cầu và mặt phẳng.
d = R
Điểm H có thuộc mặt
cầu ?
Với mọi điểm M khác H
và thuộc (P) thì M có
thuộc mặt cầu ?
Do OH = d = R nên H thuộc
mặt cầu (S).
Mọi điểm M thuộc (P) và
khác H thì OM > OH = d = R,
vậy M nằm ngoài mặt cầu (S)
Do OH = d = R nên H thuộc
mặt cầu (S).
Mọi điểm M thuộc (P) và
khác H thì OM > OH = d = R,
vậy M nằm ngoài mặt cầu (S)
Vậy (S) và (P) có duy nhất một
điểm chung H.
Ta xét trường hợp ..
.O
.H
.M

M là điểm chung của (S) và (P) khi
và chỉ khi M (P) và
O.
.H
.M
2. Vị trí tương đối giữa mặt cầu và mặt phẳng.

Cho mặt cầu S(O,R) và mp(P). Khoảng cách từ O đến (P)
bằng d. Gọi H là hình chiếu của O trên (P): OH = d
Ta xét trường hợp …
d < R
G
i
ả
s
ử
M

l
à
đ
i
ể
m

c
h
u
n
g
c
ủ
a
(
S
)
v

à
(
P
).
C
h
ứ
n
g
m
i
n
h
HMRd=−
∈
2 2 2
HM R d= −
Từ nhận xét đó hãy tìm
tập hợp các điểm chung
của (S) và (P)
M là điểm chung của (S) và (P)
M thuộc (P) và
Vậy giao của (S) và (P) là đường tròn
trong mp(P), có tâm H và bán kính
↔
2 2
HM R d= −
2 2
r R d= −
M là điểm chung của (S)

và (P) OM = R và
OH HM ( do OH (P),
HM thuộc (P) ).
Xét vuông tại H:
⊥
⊥
OHMV
2 2 2 2 2
HM OM OH R d= − = −
→
Khi (P) qua O, hãy tính
bán kính r của đường
tròn giao
Khi (P) qua O: d = 0, nên r = R.
Đường tròn giao gọi là đường tròn
lớn ( tâm O ). Mp(P): mặt phẳng kính
Mệnh đề đảo vẫn đúng. Hãy phát
biểu điều kiện cần và đủ để M là
điểm chung của (S) và (P)
.
O
.
O
R