BAI TAP MAT NON MAT TRU

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (73.82 KB, 4 trang )

(1)<div class='page_container' data-page=1>

BÀI TẬP VỀ MẶT NĨN, MẶT TRỤ.

Lớp 12B

4

Bài 1: Thiết diện qua trục của một hình nón là một tam giác vng cân có cạnh góc vng bằng a.
a) Tính diện tích xung quanh và diện tích tồn phần của hình nón.

b) Tính thể tích của khối nón tương ứng.

c) Một thiết diện qua đỉnh và tạo với đáy một góc 60o. Tính diện tích của thiết diện này.

Bài 2: Một hình nón có đường sinh là l và góc giữa đường sinh và đáy là



.
a) Tính diện tích xung quanh và thể tích khối nón.

b) Gọi I là điểm trên đường cao SO của hình nón sao cho

SO
SI

= k ( 0 < k < 1). Tính diện tích của thiết diện qua
I và vng góc với trục.

Bài 3: Cho tam giác ABC là hình chóp tam giác đều có các cạnh bên là a và có góc giữa các mặt bên và mặt đáy là



. 
Một hình nón đỉnh S có đường trịn đáy nội tiếp tam giác đều ABC, hãy tính Sxq của hình nón này theo a và



.

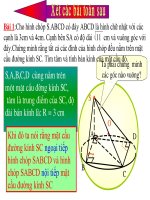
Bài 4: Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h và góc SAB =



(



> 45o). Tính S

xq của hình nón đỉnh S

và có đường trịn đáy ngoại tiếp hình vuông ABCD.

Bài 5: Cho tam giác ABC vuông tại A, AB = c, AC = b. Tính thể tích của khối trịn xoay sinh bởi tam giác đó khi quay

quanh cạnh BC.

Bài 6: Một hình thang cân ABCD có các cạnh đáy AB = 2a, DC = 4a, cạnh bên AD = BC = 3a. Cho hình thang đó (kể 
cả các điểm trong) quay quanh trục đối xứng của nó. Hãy tính thể tích và diện tích tồn phần của khối trịn xoay được 
tạo thành.

Bài 7: Cho tam giác ABC vuông tại A, AB = c, AC = b. Gọi V1, V2, V3 là thể tích các khối trịn xoay sinh bởi tam giác đó

(kể cả các điểm trong) khi lần lượt quay quanh AB, AC, BC.
a) Tính V1, V2, V3 theo a, b, c.

b) CMR: 2

2
2
1
2
3

1
1
1

V
V

V  

Bài 8: Một khối trụ có bán kính r = 5cm, khoảng cách hai đáy bằng 7cm. Cắt khối trụ bởi 1 mp song song với trục và 
cách trục 3cm. Tính diện tích của thiết diện.

Bài 9: Một hình trụ có bán kính đáy r = 53, khoảng cách giữa hai đáy h = 56. Một thiết diện song song với trục là hình 
vng. Tính khoảng cách từ trục đến mp thiết diện.

Bài 10: Một khối trụ có chiều cao bằng 20cm và có bán kính đáy bằng 10cm. Người ta kẻ hai bán kính OA và O’B’ lần 
lượt trên hai đáy sao cho chúng hợp với nhau 1 góc 30o. Cắt khối trụ bởi 1 mp chứa đường thẳng AB’ và song song với

</div>
(2)<div class='page_container' data-page=2>

Bài 11: Cho hình trụ bán kính đáy r, chiều cao OO’ = h, A và B là hai điểm thay đổi trên hai đường trịn đáy sao cho độ 
dài AB = a khơng đổi (h < a < h 2 4r2 ).

a) CM góc giữa hai đường thẳng AB và OO’ khơng đổi.

b) CM khoảng cách giữa hai đường thẳng AB và OO’ khơng đổi.
Bài 12: Một hình trụ có bán kính r có thiết diện qua trục là 1 hình vng.

a) Tính Sxq và Stp của hình trụ.

b) Tính V khối trụ tương ứng.

c) Tính thể tích của khối lăng trụ tứ giác đều nội tiếp trong khối trụ đã cho.

Bài 13: Một hình trụ có bán kính r và đường cao bằng r 3. A và B là hai điểm trên hai đường trịn đáy sao cho góc 
hợp bởi AB và trục của hình trụ là 30o.

a) Tính Sxq và Stp của hình trụ.

b) Tính V khối trụ tương ứng.

c) Tính khoảng cách giữa AB và trục của hình trụ.

Bài 14: Cho hình trụ bán kính r, chiều cao h. Gọi A và B là hai điểm lần lượt nằm trên hai đường tròn đáy (O , r) và 
(O’ , r) sao cho OA và O’B hợp với nhau một góc bằng x và góc (AB, O’O) = y.

a) Tính bán kính r theo h, x, y.

b) Tính Sxq, Stp và thể tích của khối trụ theo h, x, y.

Bài 15: Một khối trụ có các đáy là hai hình trịn tâm O và O’, bán kính r và có đường cao h = r 2 . Gọi A, B lần lượt là

một điểm trên đường tròn tâm O và đường tròn tâm O’ sao cho OA



O’B.

a) CMR các mặt bên của tứ diện OABO’ là những tan giác vng. Tính tỉ số thể tích của khối tứ diện OABO’ 
và khối trụ.

b) Gọi (



) là mp qua AB và song song OO’. Tính khoảng cách giữa trục OO’ và mp (



).
c) CMR (



) là tiếp diện của mặt trụ có trục OO’ và có bán kính đáy bằng

2
2

r .

Bài 16: Một mặt phẳng đi qua trục của hình trụ T, cắt hình trụ theo thiết diện là hình vuông cạnh 2r.
a) Tính Tính Sxq và Stp của hình trụ T.

b) Tính V khối trụ T.

c) Tính V khối lăng trụ tứ giác đều nội tiếp hình trụ T.
TỐN TRẮC NGHIỆM:

Câu 1: Một mp (P) đi qua đỉnh của một khối nón N, thiết diện của (P) với N là:

A) Hình vng B) Hình tam giác C) Hình chữ nhật D) Hình trịn.

Câu 2: Một mp (P) vng góc với trục của một khối nón N, thiết diện của (P) với khối nón N là:
A) Hình vng B) Hình tam giác C) Hình chữ nhật D) Hình trịn.

Câu 3: Quay tam giác ABC vuông tại A lần lượt quanh các trục AB và AC ta được:
(I) Hai khối nón có diện tích xung quanh bằng nhau.

</div>
(3)<div class='page_container' data-page=3>

Mệnh đề nào đúng?

A) (I) đúng, (II) sai. B) (I) sai, (II) đúng.
C) Cả (I) và (II) đều đúng. D) Cả (I) và (II) đều sai.

Câu 4: Cho tam giác ABO vuông tại O, có góc A = 30o, AB = a. Quay tam giác ABO quanh trục AO ta được một hình

nón có diện tích xung quanh bằng:
A)

a

 B) a2

 C)

a

 D) 2 a2

 .

Câu 5: Diện tích xung quanh của hình nón có chiều cao h = 16 và bán kính đáy r = 12 là:
A) 240 B) 120 C) 80 D) Đáp số khác.

Câu 6 : Cho N1 là khối nón có đỉnh S và chiều cao SO. I là trung điểm của SO. Gọi N2 là khối nón có đỉnh S, đường cao

SI và có góc ở đỉnh bằng góc ở đỉnh khối nón N1. Khi đó tỉ số thể tích của hai khối nón N1 và N2 bằng:

A) 16 B) 8 C) 4 D) 12.

Câu 7: Biết nửa góc ở đỉnh của một khối nón là 45o. Chiều cao h = 5cm. Xét các mệnh đề:

(I) Diện tích xung quanh của hình nón bằng 25 2 cm2

(II) Thể tích khối nón baèng: 
3
125

cm3.

A) (I) đúng, (II) sai. B) (I) sai, (II) đúng.

C) Cả (I) và (II) đều đúng. D) Cả (I) và (II) đều sai.

Câu 8: Cho khối nón N có thể tích V = 16cm3. Một mp (P) song song với đáy và đi qua trung điểm của đường cao của

khối nón N. Thể tích phần khối nón giữa đáy và mp (P) bằng:

A) 8cm3 B) 10cm3 C) 12cm3 D) 14cm3.

Câu 9: Một khối nón có diện tích đáy bằng 25 cm2 và thể tích bằng

3
125

cm3. Khi đó đường sinh của khối nón

bằng:

A) 2 5cm B) 5 2cm C) 5cm D) Đáp số khác.

Câu 10: Một mp (P) đi qua trục của một khối trụ T, thiết diện của (P) với khối trụ T là:
A) Hình vng B) Hình tam giác C) Hình chữ nhật D) Hình trịn.
Câu 11: Một mp (P) vng góc với trục của một khối trụ T, thiết diện (P) với khối trụ T là:

A) Hình vng B) Hình tam giác C) Hình chữ nhật D) Hình trịn.
Câu 12: Quay hình chữ nhật ABCD lần lượt quanh trục AB và BC, ta được:

(I) Hai khối trụ có thể tích bằng nhau

(II) Hai khối trụ có diện tích xung quanh bằng nhau.
Mệnh đề nào đúng?

A) (I) đúng, (II) sai. B) (I) sai, (II) đúng.
C) Cả (I) và (II) đều đúng. D) Cả (I) và (II) đều sai.

Câu 13: Cho hai điểm cố định A, B. Tập hợp các điểm M trong không gian sao cho diện tích S của



MAB khơng đổi

</div>
(4)<div class='page_container' data-page=4>

A) Mặt nón đỉnh A. B) Mặt nón đỉnh B.
C) Mặt trụ có trục là AB và bán kính R =

AB
S

. D) Mặt trụ có trục là AB và bán kính R =

AB
S

2
.
Câu 14: Cho hình trụ có bán kính đáy và chiều cao bằng r. Một hình vng ABCD có hai cạnh AB và CD lần lượt là 
các dây cung của hai đường trịn đáy, cạnh AD và BC khơng phải là đường sinh. Cạnh của hình vng ABCD là:

A) r 10 B) r

10 C) r

5 D) r

2
5 .

Câu 15: Cho hình trụ có bán kính đáy r = 2, chiều cao h = 3. Xét các mệnh đề:
(I) Diện tích xung quanh của hình trụ là: 12



.

(II) Diện tích tồn phần của hình trụ là: 16



.
(III) Thể tích khối trụ là 12



.

Mệnh đề nào đúng?

A) Chæ (I) và (II). B) Chỉ (I) và (III).
C) Chỉ (II) và (III). D) Cả (I), (II) và (III).

Câu 16: Một hình trụ có diện tích xung quanh bằng 20



và chiều cao h = 5. Thể tích của khối trụ laø:

A) 20



B) 12



C) 25



D) 16



.

Câu 17: Cho khối trụ có thể tích là V = 63



cm3 và bán kính đáy r = 3cm. Xét các mệnh đề:

(I) Diện tích xung quanh của hình trụ bằng 42



cm2.

(II) Diện tích tồn phần của hình trụ bằng 60



cm2.

Mệnh đề nào đúng?

A) (I) đúng, (II) sai. B) (I) sai, (II) đúng.
C) Cả (I) và (II) đều đúng. D) Cả (I) và (II) đều sai.

Câu 18: Hai hình chữ nhật ABCD và EFGH có cạnh AB = 3, BC = 4, EF = 12, FG = 2. Cho hình thứ nhất quay quanh

trục CD và hình thứ hai quanh trục GH. Gọi S1, S2 và V1, V2 lần lượt là diện tích xung quanh và thể tích của hai khối trụ

tương ứng. Xét các mệnh đề:

(I) S1 = S2 (II) V1 = V2

Mệnh đề nào đúng?

A) (I) đúng, (II) sai. B) (I) sai, (II) đúng.
C) Cả (I) và (II) đều đúng. D) Cả (I) và (II) đều sai.
C

âu 19: Cho khối trụ có bán kính đáy r = 5, thể tích V = 100



. Cắt khối trụ bằng một thiết diện ABCD song song với 
trục và có cạnh AB nằm trong hình trịn đáy tâm O với góc AOB = 120o. Diện tích của thiết diện là:

A) 10 B) 20 C) 10 3 D) 20 3.

Câu 20: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Diện tích xung quanh của hình nón trịn xoay sinh bởi 
đường chéo AC’ khi quay quanh AA’ bằng:

A) a2 6

 B) a2 3 C) 2 2

a

 D) a2 5.

Câu 21: Một khối tứ diện đều nội tiếp trong một khối nón. Thể tích khối nón là:

A) 3

3 a

 B) 3

6 a

 C) 3

3 a

 D) 3