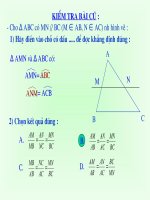khai niem tam giac dong dang

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (696.74 KB, 15 trang )

(1)<div class='page_container' data-page=1>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

TI T D Y HỘI GIẢNG

Ế

Ạ

Mơn: TỐN 8

</div>
(2)<div class='page_container' data-page=2>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
a) Định nghĩa

. ?1 a) Nhìn vào hình vẽ
hãy viết các cặp góc
bằng nhau

b) Tính các tỉ số
rồi so sánh các tỉ
số đó.
CA
A
C
BC
C
B
AB
B

A ' '

;
'
'
;
'

Trả lời: A’B’C’ và ABC có Â = Â’, B = B’,

C = C’ và thì ta nói A’B’C’ đồng

dạng với ABC

CA
A
C
BC
C
B
AB
B

A' ' ' ' ' '




H: Vậy khi nào A’B’C’ đồng dạng với ABC ?

1) Tam giác đồng dạng

</div>
(3)<div class='page_container' data-page=3>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
a) Định nghĩa

Tam giác A’B’C’ đồng dạng với ABC nếu:

CA
A
C
BC
C
B
AB
B

A' ' ' ' ' '



k
CA
A
C
BC
C
B
AB
B
A


 ' ' ' '
'
'

Ta kí hiệu tam giác đồng dạng như sau:

 A’B’C’ s ABC

Khi viết  A’B’C’ ABC ta viết theo thứ tự

cặp đỉnh tương ứng ,k gọi
là tỉ số đồng dạng

1) Tam giác đồng dạng

</div>
(4)<div class='page_container' data-page=4>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
H: Em hãy chỉ ra các

đỉnh tương ứng, các
góc tương ứng và các
cạnh tương ứng khi

A’B’C’ s ABC

Lưu ý: Khi viết tỉ số k của  A’B’C’ đồng dạng

với ABC thì cạnh của tam giác thứ nhất

(A’B’C’) viết trên, cạnh của tam giác ( ABC)

viết dưới.

Trong ?1 trên k = A'ABB' 21

1) Tam giác đồng dạng
a) Định nghĩa

3

2 2,5
6

5
4

C C'

</div>
(5)<div class='page_container' data-page=5>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
Bài tập: Cho MNQ s EFU

a) Từ định nghĩa tam giác đồng dạng ta có
những điều gì?

UE
QM
FU

NQ
EF

MN






QM
UE
NQ

FU
MN

EF

b) Hỏi EFU có đồng dạng với MNQ khơng? 
Vì sao?

k
1

 EFU MNQ

và

MNQ EFU  M = E, N = F, Q = U

và

</div>
(6)<div class='page_container' data-page=6>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
b) Tính chất.

H: Em có nhận xét
gì về quan hệ của
hai tam giác bên?
Hỏi hai tam giác có
đồng dạng với nhau
khơng? Tại sao?

CA
A
C
BC

C
B
AB

B

A' ' ' ' ' '




a) Định nghĩa

Trả lời: A’B’C’ = ABC (c.c.c)

Â = Â’, B = B’, C = C’ và = 1
 A’B’C’ ABC ( đ/n tam giác đồng dạng)

B C B' C'

</div>
(7)<div class='page_container' data-page=7>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
b) Tính chất. A

B C B' C'

- Hai tam giác bằng
nhau thì đồng dạng
với nhau và tỉ số

đồng dạng k = 1

H: Nếu A’B’C’ ABC theo tỉ số k thì
ABC có đồng dạng với A’B’C’ không?

ABC sA’B’C’ theo tỉ số nào?

Trả lời: Nếu A’B’C’ sABC thì ABC s A’B’C’

Có thì k

AB
B
A



'
'



'
'B
A

AB

</div>
(8)<div class='page_container' data-page=8>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

Tính chất 1: Hai tam giác bằng nhau thì

đồng dạng với nhau (mỗi tam giác đồng dạng 
với chính nó) và tỉ số đồng dạng k = 1

b) Tính chất.

Tính chất 2: Nếu A’B’C’ ABC thì

ABC s A’B’C’

Cho A’B’C’ A’’B’’C’’ 
và A’’B’’C’’ s A’B’C’

H: Có nhận xét gì về quan hệ giữa A’B’C’ và
ABC Trả lời: A’B’C’ s ABC

Tính chất 3: A’B’C’ A’’B’’C’’

và A’’B’’C’’ A’B’C’ thì A’B’C’ ABC

s s

a) Định nghĩa

1) Tam giác đồng dạng

B
A

C B''
A''

C'' B'
A'

</div>
(9)<div class='page_container' data-page=9>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
b) Tính chất.

a) Định nghĩa

1) Tam giác đồng dạng

Hãy phát biểu hệ quả của định lí Ta-lét
Nếu một đường cắt hai

cạnh của một tam giác và
song song với cạnh cịn lại
thì nó tạo thành một tam

giác mới có ba cạnh tương

ứng tỉ lệ với ba cạnh của
tam giác đã cho.

N
M

</div>
(10)<div class='page_container' data-page=10>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

N
M

GT MABC, MN//BC, AB, NAC

Ta có ba cạnh của AMN tương ứng tỉ lệ với

ba cạnh của ABC

H: Em có nhận xét gì thêm về quan hệ của

AMN và ABC. Trả lời: AMN s ABC

</div>
(11)<div class='page_container' data-page=11>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

N
M

GT MABC, MN//BC, AB, NAC

Có

CA
NA
BC

MN
AB

AM



 (Hệ quả của định lí Ta-lét)

 AMN ABC (theo đ/n tam giác đồng dạng)

Có MN // BC  AMN = B (đồng vị)

</div>
(12)<div class='page_container' data-page=12>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
b) Tính chất.

a) Định nghĩa

1) Tam giác đồng dạng

2. Định lí.

Nếu một đường thẳng cắt hai cạnh của tam 
giác và song song với cạnh còn lại thì nó tạo 
thành một tam giác mới đồng dạng với tam 
giác đã cho.

N M
A

B C

a A

B C

N
M

a
* Chú ý:

</div>
(13)<div class='page_container' data-page=13>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG

N
M

GT MABC, MN//BC, AB, NAC

CA
NA
BC

MN
AB

AM



 (Hệ quả của định lí Ta-lét)

 AMN ABC (theo đ/n tam giác đồng dạng)
AMN s ABC

Có

Có MN//BCAMN = B(đồng vị)

</div>
(14)<div class='page_container' data-page=14>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
Định lí.

Nếu một đường thẳng cắt hai cạnh của tam 
giác và song song với cạnh cịn lại thì nó tạo 
thành một tam giác mới đồng dạng với tam 
giác đã cho.

H: Theo định lí trên, nếu muốn AMN ABC

theo tỉ số k = ta xác định điểm M, N như thế
nào?

2
1

C
N

T.lời: Muốn AMN ABC

theo tỉ số k = thì M, N phải là
trung điểm của AB và AC2

</div>
(15)<div class='page_container' data-page=15>

KHÁI NIỆM HAI TAM GIÁC ĐỒNG DẠNG
Bài 1. Trong hai mệnh đề sau đây, mệnh đề
nào đúng? Mệnh đề nào sai?

a) Hai tam giác bằng nhau thì đồng dạng
với nhau.

b) Hai tam giác đồng dạng với nhau thì bằng
nhau.

</div>

khai niem tam giac dong dang

<b>TI T D Y HỘI GIẢNG</b>

<b>Ế</b>

<b>Ạ</b>

<b>Mơn: TỐN 8</b>

Tài liệu liên quan

Tài liệu bạn tìm kiếm đã sẵn sàng tải về