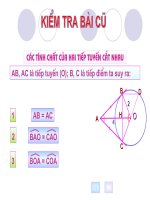
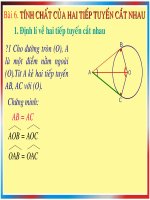Tinh chat 2 tiep tuyen cat nhau

<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>

TRngTHCSiỏngThanhtrỡ-Hni
TRngTHCSiỏngThanhtrỡ-Hni

Hội thi giáo viên giỏi cấp huyện Môn Toán

</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

TRngTHCSiỏngThanhtrỡ-Hni
TRngTHCSiỏngThanhtrỡ-Hni

Hội thi giáo viên giỏi cấp huyện Môn Toán

Hội thi giáo viên giỏi cấp huyện Môn To¸n - - Hun Thanh Tr× 11/2008Hun Thanh Tr× 11/2008

</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

<b>C</b>

<b>O</b>
<b>B</b>

<b>Cho hình vẽ, trong đó AB, AC theo </b>
<b>thứ tự là tiếp tuyến tại B, tại C của </b>
<b>đ ờng tròn (O). Hãy kể tên một vài </b>
<b>đoạn thằng bằng nhau, một vài góc </b>
<b>bằng nhau trong hình.</b>

<b>Bµi tËp ?1_SGK</b>

o
90
ˆ

ˆ __C _

B
<b>2</b>
<b>1</b>
<b>2</b>
<b>1</b>

R

OC

OB





AC

AB 

2
Aˆ
1

Aˆ 

2
Oˆ
1

Oˆ

Điền tiếp thông tin vào chỗ trống:

Điền tiếp thông tin vào chỗ trống:

A cỏch u hai tip im...v ...
Tia AO là tia ...của góc BAC
Tia OA là tia phõn giỏc ca gúc ...

B C

phân giác

BOC

Nếu hai tiếp tuyến tại B và tại C của đ ờng tròn tâm
O cắt nhau tại A

Nếu hai tiếp tuyến tại B và tại C của đ ờng tròn tâm
O cắt nhau tại A

Thì

Thì

</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

<b>Tiết 28: tính chất của hai tiếp tuyến cắt nhau</b>

<b>1. Định lí về hai tiÕp tun c¾t nhau :</b>

<b>NÕu hai tiÕp tun cđa một đ ờng tròn cắt nhau tại một điểm thì :</b>

<b>C</b>

<b>O</b>
<b>B</b>

<b>2</b>
<b>1</b>

<b>2</b>
<b>1</b>

<b>Tia kẻ từ tâm đi qua điểm đó là tia phân giác của </b><i><b>góc tạo </b></i>
<i><b>bởi hai bán kính</b></i><b> đi qua các </b><i><b>tiếp điểm</b></i><b>.</b>

<b>Tia kẻ từ tâm đi qua điểm đó là tia phân giác của </b><i><b>góc tạo </b></i>
<i><b>bởi hai bán kính</b></i><b> đi qua các </b><i><b>tiếp điểm</b></i><b>.</b>

<b>Điểm đó cách đều hai </b><i><b>tip im.</b></i>

<b>im ú cỏch u hai </b><i><b>tip im.</b></i>

<b>Định lí:</b>

<b>Tia kẻ từ điểm đó đi qua tâm là tia phân giác của </b><i><b>góc </b></i>
<i><b>tạo bởi hai tiếp tuyến.</b></i>

<b>Tia kẻ từ điểm đó đi qua tâm là tia phân giác của </b><i><b>góc </b></i>
<i><b>tạo bởi hai tiếp tuyến.</b></i>

</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

<b>TiÕt 28: tính chất của hai tiếp tuyến cắt nhau</b>

<b>1. Định lí về hai tiếp tuyến cắt nhau :</b>

<b>C</b>
<b>O</b>
<b>B</b>
<b>2</b>
<b>1</b>
<b>2</b>
<b>1</b>
GT
KL

AB và AC là các tiếp tuyến
tại B và tại C của (O;R)

a. AB = AC
b. Â₁ = Â₂
c. Ô₁ = Ô₂

<b>A</b>
<i>Chứng minh</i>
<b>.</b>
<b>2</b>
<b>O</b>
<b>1</b>
<b>O</b>
<b> ,</b>
<b>2</b>
<b>A</b>
<b>1</b>

<b>A</b>
<b> AC,</b>
<b> AB</b>
<b>)</b>
<b>(</b>
<b>ACO</b>
<b>ABO</b>
<b>chung</b>
<b>OA </b>
<b>R</b>
<b>OC</b>
<b>OB</b>
<b>: </b>
<b>ACO</b>
<b>ABO</b>






900
C

vuông
góc
cạnh

-huyền
cạnh
B
có
và
Xét

</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

<b>Tiết 28: Tính chất của hai tiếp tuyến cắt nhau</b>

<b>1. Định lí về hai tiếp tuyến cắt nhau :</b>

<b>C</b>

<b>O</b>
<b>B</b>

<b>2</b>
<b>1</b>

<b>2</b>
<b>1</b>

GT
KL

AB và AC là các tiếp tuyến
tại B và tại C của (O;R)

a. AB = AC
b. Â₁ = Â₂
c. Ô₁ = Ô₂

</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

<b>TiÕt 28: tÝnh chÊt cña hai tiÕp tuyÕn cắt nhau</b>

<b>1. Định lí về hai tiếp tuyến cắt nhau :</b>

<b>C</b>

<b>O</b>
<b>B</b>

<b>2</b>
<b>1</b>

<b>2</b>
<b>1</b>

</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

<b>Bµi tËp ?2_SGK</b>

</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

H y vÏ thªm 1 tiếp tuyến a tại D của đ ờng tròn <b>·</b>
t©m O sao cho a cắt cả 2 tiếp tuyến đ cho<b>Ã</b>

H y vÏ thªm 1 tiếp tuyến a tại D của đ ờng tròn <b>·</b>

t©m O sao cho a cắt cả 2 tiếp tuyến đ cho<b>·</b>

<b>Bµi tËp 2</b>

<b>A</b>

<b>M</b>

<b>N</b>
<b>O</b>

<b>C</b>
<b>B</b>

<b>D</b>

</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

H y vÏ thªm 1 tiÕp tuyÕn a tại D của đ ờng tròn <b>Ã</b>
tâm O sao cho a cắt cả 2 tiếp tuyến đ cho<b>Ã</b>

H y vÏ thªm 1 tiÕp tuyÕn a tại D của đ ờng tròn <b>·</b>

t©m O sao cho a cắt cả 2 tiếp tuyến đ cho<b>Ã</b>

<b>A</b>

<b>E</b> <b>F</b>

<b>O</b>

<b>C</b>
<b>B</b>

<b>D</b>
<b>a</b>

</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

H y vẽ thêm 1 tiếp tuyến a tại D của đ êng trßn <b>·</b>
tâm O sao cho a cắt cả 2 tiếp tuyến ® cho<b>·</b>

H y vẽ thêm 1 tiếp tuyến a tại D của ® êng trßn <b>·</b>

tâm O sao cho a cắt cả 2 tiếp tuyến đ cho<b>Ã</b>

<b>Bài tập 2</b>

<b>A</b>
<b>M</b>
<b>N</b>
<b>O</b>
<b>C</b>
<b>B</b>
<b>D</b>
<b>a</b>
<b>Khi ú:</b>

a) Do B, C, D là các tiếp điểm nên

a) Do B, C, D là các tiếp điểm nªn

OB = OC =... = R

OB = OC =... = R

b) áp dụng tính chất của 2 tiếp tuyến cắt
nhau, ta cã:

b) ¸p dơng tÝnh chÊt cđa 2 tiÕp tuyến cắt
nhau, ta có:

AO là ... của góc BAC

AO là ... của góc BAC

MO là tia phân giác của ...

MO là tia phân giác của ...
... là tia phân giác của góc DNC

... là tia phân giác của góc DNC

c) Đ ờng tròn tâm O ...với 3 cạnh của tam giác MNA

c) Đ ờng tròn tâm O ...với 3 cạnh của tam giác MNA

OD

OD

tia phân giác
tia phân giác

gãc BMC
gãc BMC
NO

NO
tiÕp xóc
tiÕp xúc

Đ ờng tròn tâm O là đ ờng tròn nội tiÕp tam gi¸c AMN

</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>

<b>A</b>

<b>C</b>

<b>I</b>

<b>E</b>
<b>F</b>

<b>D</b>
<b>TiÕt 28: tÝnh chÊt của hai tiếp tuyến cắt nhau</b>

<b>1. Định lí về hai tiếp tuyến cắt nhau:</b>

<b>2. Đ ờng tròn nội tiếp tam giác</b>

<i><b>+ </b><b>Đ ờng tròn nội tiếp tam giác</b><b> là </b><b>đ </b></i>
<i><b>ờng tròn tiếp xúc với ba cạnh của tam </b></i>
<i><b>giác</b><b>.</b></i>

<i><b>+ Tâm này </b><b>cách đều ba cạnh của tam </b></i>
<i><b>giác</b><b>. </b></i>

</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13>

H y vẽ thêm 1 tiếp tuyến a tại D của ® êng trßn <b>·</b>
tâm O sao cho a cắt cả 2 tiếp tuyÕn ® cho<b>·</b>

H y vẽ thêm 1 tiếp tuyến a tại D của đ ờng tròn <b>Ã</b>

tâm O sao cho a cắt cả 2 tiếp tuyến đ cho<b>Ã</b>

<b>Bài tập 2</b>

<b>A</b>
<b>E</b> <b>F</b>
<b>O</b>
<b>C</b>
<b>B</b>
<b>D</b>
<b>a</b>
<b>Khi ú:</b>

a) Do B, C, D là các ... nªn

a) Do B, C, D là các ... nên

OB = OC =OD = R

OB = OC =OD = R

b) ¸p dơng tÝnh chất của 2 tiếp tuyến cắt
nhau, ta có:

b) áp dơng tÝnh chÊt cđa 2 tiÕp tun c¾t
nhau, ta cã:

AO lµ ... cđa gãc BAC

AO lµ ... cđa gãc BAC
EO là tia phân giác của ...

EO là tia phân giác của ...
... là tia phân giác của góc DFC

... là tia phân giác của góc DFC

c) Đ ờng tròn tâm O tiếp xúc với cạnh ... và phần kéo dài của 2
cạnh ...và ...của tam giác AEF

c) Đ ờng tròn tâm O tiếp xúc với cạnh ... và phần kéo dài của 2
cạnh ...và ...của tam giác AEF

tia phân giác
tia phân giác

gãc BED
gãc BED
FO
FO
tiÕp ®iĨm
EF
EF
AE

AE AF AF

Đ ờng tròn tâm O là đ ờng tròn bàng tiếp trong góc A của
tam giác AEF

</div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>

<b>A</b>

<b>B</b> <b>C</b>

<b>K</b>
<b>D</b>

<b>E</b>
<b>F</b>

<b>x</b> <b>y</b>

</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15>

<b>A</b>

<b>B</b> <b>C</b>

<b>O₁</b>
<b>O₃</b>

</div>
<span class='text_page_counter'>(16)</span><div class='page_container' data-page=16></div>
<span class='text_page_counter'>(17)</span><div class='page_container' data-page=17>

<b>Hãy nối mỗi ô ở cột trái với một ô ở cột phải để đ </b>
<b>ợc khng nh ỳng</b>

<b>1. Đ ờng tròn nội </b>

<b>tip tam giỏc</b> <b>a. Là đ ờng tròn đi qua ba đỉnh của tam giác</b>
<b>2. Đ ờng trịn bàng </b>

<b>tiÕp tam gi¸c</b> <b>b. Là đ ờng tròn tiếp xúc với ba cạnh của tam giác</b>
<b>3. Đ ờng tròn ngoại </b>

<b>tiếp tam giác</b> <b>c. Là giao điểm ba đ ờng phân giác trong của tam </b>
<b>giác</b>

<b>4. Tâm của đ ờng </b>
<b>tròn nội tiếp tam </b>
<b>giác</b>

<b>d. Là đ ờng tròn tiếp xúc với </b>
<b>một cạnh của tam giác và </b>
<b>phần kéo dài của hai cạnh </b>
<b>kia</b>

<b>5. Tâm của đ ờng </b>
<b>tròn bàng tiếp tam </b>
<b>giác</b>

<b>e. Là giao điểm hai đ ờng </b>
<b>phân giác ngoài của tam </b>
<b>gi¸c</b>

<b>1 - b</b>

<b>2 - d</b>

<b>3 - a</b>

<b>4 - c</b>

<b>5 - e</b>

</div>
<span class='text_page_counter'>(18)</span><div class='page_container' data-page=18>

BD
CA

a) CM = ; DM =

Cho hình vẽ sau

AB là ® êng kÝnh cđa ® êng trßn
(O)

AC ; CD ; BD là các tiếp tuyến
của đ ờng tròn (O) tại A ; M và B.

A _B

C

D
M

O

x y <i><b>Điền nội dung thích hợp vào </b></i>
<i><b>chỗ trống: </b></i>

b) = CA + BD

c) OC là tia phân giác của góc
CD

MOA

</div>
<span class='text_page_counter'>(19)</span><div class='page_container' data-page=19>

A

B x

C y

O

B’

C’
O’

<b>Gọi O là tâm đ ờng trịn bất kỳ tiếp xúc với 2 cạnh của </b>

<b>góc xAy. Khi đó góc OAx bằng góc OAy</b>

</div>
<span class='text_page_counter'>(20)</span><div class='page_container' data-page=20>

Nắm vững định lí trong SGK

Nắm vững định lí trong SGK

BTVN: 26,27,28,29 SGK

</div>
<span class='text_page_counter'>(21)</span><div class='page_container' data-page=21>

Xin chân thành cảm ơn

</div>

<!--links-->