Tiết 44. Góc có đỉnh bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn

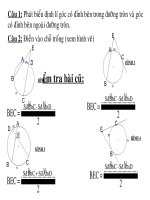
KI M TRA BÀI CŨỂ :
- Xác định góc ở tâm, góc nội tiếp, góc tạo bởi tia
tiếp tuyến và dây cung.
- Viết hệ thức liên hệ giữa số đo của mỗi góc trên
với số đo của cung bị chắn tương ứng

Cho hình vẽ:
Tit 44 Đ5. GểC Cể NH BấN TRONG NG TRềN
GểC Cể NH BấN NGOI NG TRềN
HèNH HC
1. GểC Cể NH BấN TRONG NG TRềN
VD: Góc BEC là góc có đỉnh ở bên trong đường tròn.
Hai cung BnC v AmD gọi là hai cung bị chắn.
nh lý: S o ca gúc cú nh bờn trong ng
trũn bng na tng s o hai cung b chn
Góc BEC là góc có đỉnh ở bên trong đường tròn (o)

Chng minh:

GT:
KL:
c im:
Hỡnh 31
( S dng gúc ngoi ca tam giỏc)
Cú nh nm bờn trong ng trũn v
cú hai cung b chn
Bài tập vận dụng ( Bài 36 tr 82 SGK)
Cho đường tròn tâm O và hai dây AB, AC.
Gọi M, N lần lượt là điểm chính giữa của
cung AB và AC. Đường thẳng MN cắt dây AB

tại E và cắt dây AC tại H. Chứng minh tam
giác AEH là tam giác cân.
Chứng minh:
2. GểC Cể NH BấN NGOI NG TRềN
VD( H33): Góc BEC là góc có đỉnh ở bên ngoài đường tròn,
Các cung nhỏ AD, BC là các cung bị chắn.
nh lý: S o ca gúc cú nh bờn ngoi ng
trũn bng na hiu s o hai cung b chn
c im:
GT:
KL:
Góc BEC là góc có đỉnh ở bên ngoi đường tròn (o)
Chng minh: ( S dng gúc ngoi ca tam giỏc)
nh nm ngoi ng trũn, cỏc cnh u cú im chung vi ng
trũn;cú hai cung b chn
H33
GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN
GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
n
m
E
O
C
A
B
D
* Đặc điểm:
-
Có đỉnh nằm bên trong đường tròn
-

Có 2 cung bị chắn
* Đặc điểm:
-Có đỉnh nằm bên ngoài đường tròn, các
cạnh đều có điểm chung với đường tròn
-
Có 2 cung bị chắn
* Định lý: Số đo của góc có đỉnh ở
bên trong đường tròn bằng nửa tổng
số đo hai cung bị chắn
* Định lý: Số đo của góc có đỉnh ở
bên ngoài đường tròn bằng nửa
hiệu số đo hai cung bị chắn

n

m

D

A

O

C

E

B

Bài tập vận dụng :

b/
Bài giải:
a/ c,
Vậy
Từ một điểm A ở ngoài đường tròn (O), vẽ hai cát tuyến ABC và AMN ( B nằm giữa A
và C, M nằm giữa A và N ), H là giao điểm của BN và CM .
0 0
ˆ
50 , 40A sdBM
= =
)
Chứng minh rằng:
BN CM
⊥
c/Cho biết
a/ Tìm những góc có đỉnh ở bên trong đường tròn và viết hệ thức liên hệ số
đo mỗi góc trên với số đo các cung bị chắn tương ứng
b/ Tìm những góc có đỉnh ở bên ngoài đường tròn và viết hệ thức liên hệ số
đo mỗi góc trên với số đo các cung bị chắn tương ứng
- Häc thuéc c¸c kh¸i niÖm, ®Þnh lÝ.
-
Lµm c¸c bµi 37,38, 39, 40 tr 83 sgk.
-
Chu n b ti t h c sau luy n t pẩ ị ế ọ ệ ậ
H­íng dÉn vÒ nhµ.
CÁM ƠN THẦY CÔ VÀ
CÁC EM HỌC SINH ĐÃ
THAM DỰ TIẾT HỌC