Tiet 29 Tinh chat hai tiep tuyen cat nhau

<span class='text_page_counter'>(1)</span>

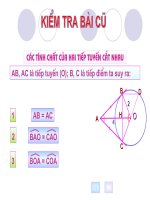
<span class='text_page_counter'>(2)</span> KIEÅM TRA BAØI CUÕ + Nêu định lí về tính chất hai tiếp tuyến cắt nhau. + Đường tròn như thế nào gọi là đường tròn ngoại tiếp tam giác và tâm của đường tròn này là giao điểm của ba đường nào trong tam giác?. P A. Đường tròn tâm O được gọi là đường tròn gì của tam giác APQ ?. B 1. 1 2. M. Đường tròn tâm O được gọi là đường tròn gì của tam giác AMN ?. O 2. Q C N.

<span class='text_page_counter'>(3)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) ?3. Tam giác ngoại tiếp đường tròn. A. ABC. AI, BI, CI lµ ph©n gi¸c c¸c gãc cña ABC. GT ID  BC ; IE  AC; IF  AB KL. D, E, F n»m trªn (I). E F I. Chứng minh:. µ  ID = IF I thuộc phân giác B. µ  ID = IE I thuộc phân giác C Neân ID = IE = IF Vaäy : D, E , F  ( I ). B. D. C Đường tròn nội tieáp tam giaùc.

<span class='text_page_counter'>(4)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) A 1. Ñònh lyù veà hai tieáp tuyeán caét nhau 2. Đường tròn nội tiếp tam giác + Đờng tròn nội tiếp tam giác là đờng trßn tiÕp xóc víi ba c¹nh cña tam gi¸c, E còn tam giác gọi là ngoại tiếp đờng tròn + Tâm của đờng tròn nội tiếp tam giác là giao điểm của ba đờng phân giác trong cña tam gi¸c.. F I B. D. C. tròn tròn như này thế là Tâm Đường của đường làba đường giao nào điểmgọi của đường nộitam tiếpgiác? tam nàotròn trong giác?.

<span class='text_page_counter'>(5)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) 1. Ñònh lyù veà hai tieáp tuyeán caét nhau CÁCH VẼ ĐƯỜNG TRÒN NỘI TIẾP TAM GIAÙC 2. Đường tròn nội tiếp tam giác + Đờng tròn nội tiếp tam giác là đờng trßn tiÕp xóc víi ba c¹nh cña tam gi¸c, còn tam giác gọi là ngoại tiếp đờng tròn + Tâm của đờng tròn nội tiếp tam giác là giao điểm của ba đờng phân giác trong cña tam gi¸c.. TAÂM. BAÙN KÍNH. A. O B. C.

<span class='text_page_counter'>(6)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) B E. A. 1. 1. 2. 2. F. O. C. Đường tròn tâm O được gọi là đường tròn gì của tam giác AEF?.

<span class='text_page_counter'>(7)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) ?4. A. ABC, BK, CK lµ ph©n gi¸c c¸c gãc ngoµi t¹i B vµ C GT KD  BC ; KE  AC; KF  AB KL. B. D. C E. D, E, F n»m trªn (K). F. Chứng minh:. ·  ph©n gi¸c xBC  KD = KF K  ph©n gi¸c ·yCB  KD = KE. K. K. x. Nªn KD = KF = KE Do đó D, E, F thuộc (K). Đường tròn bàng tieáp tam giaùc. y.

<span class='text_page_counter'>(8)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) A 1. Ñònh lyù veà hai tieáp tuyeán caét nhau 2. Đường tròn nội tiếp tam giác 3. Đường tròn bàng tiếp tam giác + §êng trßn bµng tiÕp tam gi¸c lµ ® êng trßn tiÕp xóc víi mét c¹nh cña tam gi¸c vµ tieáp xuùc vôí caùc phaàn keùo daøi cuûa hai caïnh kia. + Tâm của đờng tròn bàng tiếp tam giác là giao điểm của hai đờng phân giác ngoài, hoặc giao điểm của đờng phân giác trong và đờng phân giác ngoµi cña tam gi¸c.. B. D. C E. F y K x. Đường tròn này là Tâm của đường trònKthế này làgọi giao Đường tròntâm như nào đường tròn bàng điểm củagọi các nào của được là đường đườngtiếp tròntrong góc Atiếp của tam tam giác ?giác bàng tam giác ? ABC.

<span class='text_page_counter'>(9)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) 1. Ñònh lyù veà hai tieáp tuyeán caét nhau 2. Đường tròn nội tiếp tam giác 3. Đường tròn bàng tiếp tam giác + §êng trßn bµng tiÕp tam gi¸c lµ ® .J A êng trßn tiÕp xóc víi mét c¹nh cña tam gi¸c vµ c¸c phÇn kÐo dµi cña hai c¹nh cßn l¹i. + Tâm của đờng tròn bàng tiếp tam giác là giao điểm của hai đờng phân giác ngoài, hoặc giao điểm của đờng phân giác trong và đờng phân giác ngoµi cña tam gi¸c. + Với một tam giác, có ba đờng tròn bµng tiÕp.. .I. B F x. D. K. C. E y. Với một tam giác có bao nhiêu đường tròn bàng tiếp như vậy?.

<span class='text_page_counter'>(10)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) 1. Ñònh lyù veà hai tieáp tuyeán caét nhau 2. Đường tròn nội tiếp tam giác + Đờng tròn nội tiếp tam giác là đờng tròn tiếp xóc víi ba c¹nh cña tam gi¸c, cßn tam gi¸c gäi là ngoại tiếp đờng tròn. +Tâm của đờng tròn nội tiếp tam giác là giao điểm của ba đờng phân giác trong của tam giác.. 3. Đường tròn bàng tiếp tam giác. + Đờng tròn bàng tiếp tam giác là đờng tròn tiÕp xóc víi mét c¹nh cña tam gi¸c vµ tieáp xuùc vôí caùc phaàn keùo daøi cuûa hai caïnh kia. + Tâm của đờng tròn bàng tiếp tam giác là giao điểm của hai đờng phân giác ngoài, hoặc giao điểm của đờng phân giác trong và đờng phân gi¸c ngoµi cña tam gi¸c. + Mỗi tam giác có ba đờng tròn bàng tiếp.

<span class='text_page_counter'>(11)</span> BAØI TAÄP TRAÉC NGHIEÄM Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được một khẳng định đúng. 1/ Đường tròn nội tiếp tam giaùc. a/ là đường tròn đi qua 3 đỉnh một tam giaùc.. 1-b. 2/ Đường tròn bàng tiếp tam giaùc. b/ là đường tròn tiếp xúc với 3 cạnh cuûa moät tam giaùc.. 2-d. 3/ Đường tròn ngoại tiếp tam giaùc. c/ là giao điểm 3 đường phân giác trong cuûa moät tam giaùc.. 3-a. 4/ Tâm của đường tròn nội tieáp tam giaùc. d/ là đường tròn tiếp xúc với một caïnh cuûa tam giaùc & phaàn keùo daøi cuûa 2 caïnh kia.. 4-c. 5/ Tâm của đường tròn bàng tieáp tam giaùc. e/ là giao điểm 2 đường phân giác ngoài của một tam giác.. 5-e. f/ là giao điểm 3 đường trung trực cuûa moät tam giaùc..

<span class='text_page_counter'>(12)</span> Bµi 31 SGK tr.116: Trªn h×nh 82, tam gi¸c ABC ngo¹i tiÕp ® êng trßn (O). A a) C/m r»ng: 2AD = AB + AC - BC. b) T×m c¸c hÖ thøc t¬ng tù nh hÖ thøc ë c©u a. F D O. Gi¶i a) C/m 2AD = AB + AC - BC. B. E H×nh 82(sgk) Ta cã AD = AF, BD = BE, CF = CE (TÝnh chÊt hai tiÕp tuyÕn c¾t nhau) Ta cã AB + AC - BC = AD + DB + AF + FC - BE - EC = AD + DB + AD + FC - DB - FC = 2 AD Vậy 2 AD = AB + AC - BC. Qua bài này nếu biết được độ dài ba cạnh của tam giác ABC ngoại tiếp đường tròn (O) thì Qua bài này ta có đợc bài toán sau: ta cú thể tỡm được cỏc doạn Tính độ dài các đoạn thẳng từ đỉnh đến tiếp điểm, khi biết độ nào? thẳng. b) C¸c hÖ thøc t¬ng tự ë c©u a lµ: 2BE = BA + BC - AC 2CF = CA + CB - AB. dài 3 cạnh của tam giác ngoại tiếp đờng tròn (O).. C.

<span class='text_page_counter'>(13)</span> Đ/t và đ/tròn chỉ có 1 điểm chung. N. n ậ h. ết i b. p it ế. tu. n ế y. K/c từ tâm đtr đến đ/t bằng bán kính. hai c / T. ha n t ắ tt c. Tia p/g của góc tạo bởi 2 t/t. u. Tia p/g góc tạo bởi hai bán kính Đ/n. Đ/Tr ngoại tiếp t/g Đ /T rb àn g. Đ/T r. ti ế p. Giao điểm cách đều hai tiếp điểm. Tâm đ/tr nộ i. t iế pt. Đ/n /g. Tâm đ/tr t/g. Đ/n Tâm đ/tr.

<span class='text_page_counter'>(14)</span> HƯỚNG DẪN VỀ NHAØ -Nắm vững các tính chất tiếp tuyến của đường tròn và dấu hiệu nhận biết tiếp tuyến; -Phaân bieät ñònh nghóa, caùch xaùc ñònh taâm của các đường tròn ngoại tiếp, nội tiếp, bàng tiếp tam giác. -Laøm baøi taäp: 27, 28, 29, 30 tr 115_116 SGK; -Tieát 30 luyeän taäp..

<span class='text_page_counter'>(15)</span> GV THỰC HIỆN: NGUYỄN TIẾN.

<span class='text_page_counter'>(16)</span> TIEÁT 29: Baøi 6 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) A ?3. Tam giác ngoại tiếp đường tròn. ABC. AI, BI, CI lµ ph©n gi¸c c¸c gãc cña ABC. GT ID  BC ; IE  AC; IF  AB KL. E F I. D, E, F n»m trªn (I). Chứng minh:. µ  I thuộc phân giác B µ  I thuộc phân giácC Neân ID = IE = IF Vaäy : D, E , F  ( I ). B ID = IF ID = IE. D. C Đường tròn nội tieáp tam giaùc.

<span class='text_page_counter'>(17)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) 1. Ñònh lyù veà hai tieáp tuyeán caét nhau nhau: B 2. Đường tròn nội tiếp tam giác E A 1 1 A 2 2 O E. F. C. F I B. D. C. Đường tròn tâm O được gọi là đường tròn gì của tam giác AEF ?.

<span class='text_page_counter'>(18)</span> TIEÁT 29 TÍNH CHAÁT CUÛA HAI TIEÁP TUYEÁN CAÉT NHAU (TT) A ?4 1. Ñònh lyù veà hai tieáp tuyeán caét nhau 2. Đường tròn nội tiếp tam giác B. ABC, BK, CK lµ ph©n gi¸c c¸c gãc ngoµi t¹i B vµ C GT KD  BC ; KE  AC; KF  AB KL. D. E F. D, E, F n»m trªn (K). y. Chứng minh:. ·  ph©n gi¸c xBC  KD = KF K  ph©n gi¸c ·yCB  KD = KE K. C. K x. Nªn KD = KF = KE Do đó D, E, F thuộc (K) Đường tròn bàng tiếp tam giaùc.

<span class='text_page_counter'>(19)</span>