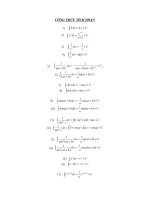công thức tích phân

NGUYÊN HÀM - TÍCH PHÂN ÔN THI ĐẠI HỌC
Phần 1. Nguyên hàm
Tìm nguyên hàm của các hàm số
1. A =

x(1 −
e
x
x
)dx =

xdx −

e
x
dx =
x
2
2
− e
x
+ C
2. B =

x
2
− x + 3
x + 1
dx =

(x − 2)dx +


5
x + 1
dx =
(x − 2)
2
2
+ 5 ln |x + 1| + C
3. C =

x
4
+ 1
x + 1
dx =


x
3
− x
2
+ x − 1 +
2
x + 1

dx =
x
4
4
−

x
3
3
+
x
2
2
+ 2 ln|x + 1| + C
4. D =

dx

(x
2
+ 1)
3
=

1
√
x
2
+ 1
x
2
+ 1
dx =

√
x

2
+ 1 −
x
2
√
x
2
+ 1
x
2
+ 1
dx =

d

x
√
x
2
+ 1

=
x
√
x
2
+ 1
+ C
5. E =


4

x
3
√
xdx =

x
1
3
dx =
3
4
x
3
√
x + C
6. F =

2
x

3
x
+
2
−x
√
x + 1


dx =


6
x
+
1
√
x + 1

x =

6
x
dx +

d(x + 1)
(x + 1)
1
2
=
6
x
ln 6
+ 2
√
x + 1 + C
7. G =

1

sin x.cos
3
x
dx =

1
cos
2
x
sin x cos x
dx =

(tan x + cot x)d(tan x) =

tan
2
x + 1
tan x
d(tan x) =
tan
2
x
2
+ln |tan x|+
C
8. H =

x
2
+ x + 1

x
3
− 3x + 2
dx =
1
3

1
x + 2
dx +
2
3

1
x − 1
dx +

1
(x − 1)
2
dx =
1
3
ln |x + 2| +
2
3
ln |x − 1| −
1
x − 1
+ C

9. K =

xdx
3
√
x + 1 −
√
x + 1

6
√
x + 1 = t ⇒ x = t
6
− 1 ⇒ dx = 6t
5
dt

10. I =

1
1 + cosx
e
x
dx +

sinx
1 + cosx
e
x
dx =


1
2cos
2
x
2
e
x
dx +

tan
x
2
e
x
dx = e
x
.tan
x
2
+ C
Chú ý:



1
2cos
2
x
2

e
x
dx =

e
x
d(tan
x
2
) = e
x
.tan
x
2
−

tan
x
2
e
x
dx


11. J =

sin x − cos x
3
√
sin x + cos x

dx =

−
d(sin x + cos x)
3
√
sin x + cos x
= −
3
2
3

(sin x + cos x)
2
+ C
12. M =

x(1 − x)
20
dx
13. N =

x
8
(x
4
− 1)
3
dx =


x
3
.x
5
(x
4
− 1)
3
dx Đặt



x
5
= u
dv =
x
3
dx
(x
4
− 1)
3
⇒



du = 5x
4
dx

v =
−1
8(x
4
− 1)
2
Vậy: N =
−x
5
8(x
4
− 1)
2
+
5
8

x
4
dx
(x
4
− 1)
2
=
−x
5
8(x
4
− 1)

2
+
5
8
.J Tiếp tục đặt



x = u
dv =
x
3
dx
(x
4
− 1)
2
⇒



du = dx
v =
−1
4(x
4
− 1)
Ta có: P =
−x
4(x

4
− 1)
+
1
4

1
x
4
− 1
dx Cuối c ùng ta đi tính: K =

1
x
4
− 1
dx =
1
2

(x
2
+ 1) − (x
2
− 1)
(x
2
+ 1)(x
2
− 1)

dx =
1
2


dx
x
2
+ 1
+

dx
x
2
− 1

Q =

π
0
x sin x
1 + cos
2
x
dx (Đề thi thử số 2-VMF)
Đặt t = π −x, ta c ó dt = −dx. Với x = 0, ta có t = π. Với x = π, ta có t = 0.
maxmin onluyentoan.vn
Do đó:
I = −
0


π
(π − t) sin(π − t)
1 + cos
2
(π − t)
dt =
π

0
(π − t) sin t
1 + cos
2
t
dt =
π

0
(π − x) sin x
1 + cos
2
x
dx = π
π

0
sin x
1 + cos
2
x

dx − I
= −π
π

0
d(cos x)
1 + cos
2
x
− I = −π
−1

1
dt
1 + t
2
− I = π
1

−1
dt
1 + t
2
− I.
Và ta thu được I =
π
2
1

−1

dt
1 + t
2
=
π
2
I
1
.
Bây giờ, ta sẽ tính I
1
: Đặt t = tan u với u ∈

−
π
2
,
π
2

, ta có dt = (1 + tan
2
u)du.
Với phép đặt này, các cận thay đổi như sau: Với t = −1, ta có u = −
π
4
. Với t = 1, ta có u =
π
4
. Như vậy,

I
1
=
π
4

−
π
4
(1 + tan
2
u)du
1 + tan
2
u
=
π
4

−
π
4
du = u|
π
4
−
π
4
=
π

2
. Cuối cùng, ta được I =
π
2
4
.
14. R =

3

3x − x
3
dx
Đặt: t =
3
√
3x − x
3
x
⇒ x
3
=
3
t
3
+ 1
⇒ 2xdx =
−9t
2
dt

(t
3
+ 1)
2
I =
1
2

3
√
3x − x
3
2xdx
x
=
−9
2

t
3
dt
(t
3
+ 1)
2
=
3
2

td(

1
t
3
+ 1
) =
3t
2(t
3
+ 1)
−
3
2

dt
t
3
+ 1
Tính I =
dt
t
3
+ 1
=

d(t + 1)
(t + 1)[(t + 1)
2
− 3(t + 1) + 3]
=
1

2
(ln3(1 − t) − 2ln 3t + ln(1 + t)) + C
15. I =

x
2
− 1
x
4
+ 1
dx
Chia cả tử và mẫu cho x
2
khi đó ta được:
I =

x
2
− 1
x
4
+ 1
dx =

1 −
1
x
2
(x +
1

x
)
2
− 2
dx
Đặt t = x +
1
x
,suy ra dt = (1 −
1
x
2
)dx
Từ đó ta sẽ có: I =

dx
t
2
− 2
=
1
2
√
2
ln |
t −
√
2
t +
√

2
| + C =
1
2
√
2
ln |
x
2
− x
√
2 + 1
x
2
+ x
√
2 + 1
| + C
16.

√
x
3
+ x
2
x
dx
I =

√

x
3
+ x
2
x
dx =

|x|
√
x + 1
x
dx
Với x ∈ (0; +∞) ta được
I =

√
x + 1dx =
2
3
(x + 1)
√
x + 1 + C
Với x ∈ (−∞; 0) ta được
I = −

√
x + 1dx = −
2
3
(x + 1)

√
x + 1 + C
17. I =

cos 2x
cos x −
√
3. sin x
dx
cos x −
√
3 sin x = 2.

1
2
. cos x −
√
3
2
. sin x

= 2. cos

x +
π
3

I =

cos 2x

cos x −
√
3 sin x
dx =

cos 2x
2. cos

x +
π
3

dx
x +
π
3
= t ⇔ dx = dt. Suy ra: I =
1
2
.

cos

2t −
2π
3

cos t
dt I =
1

2

cos 2t.

−
1
2

+ sin 2t.

√
3
2

cos t
dt
18. I =

1
0
1
(x
2
+ 1)
√
x
2
+ 3
dx
maxmin onluyentoan.vn

Trước tiên, ta đổi biến số t =

x
2
+ 1
x
2
+ 3
⇒









x =

1 − 3t
2
t
2
− 1
dx =
2t

1−3t
2

t
2
−1
· (t
2
− 1)
2
dt
Do hàm dưới dấu tích phân liên tục trên [0, 1], ta chuyển thành tích phân bất định để dễ trình bày. Thế kết quả
trên vào tích phân đầu bài:
I =

2t

1−3t
2
t
2
−1
· (t
2
− 1)
2
·
t

2t
2
1−t
2


3/2
dt
=
1
√
2

dt
t
√
3t
2
− 1
Nếu đặt u =
√
3t
2
− 1, ta dễ dàng thấy được tích phân này chính bằng
1
√
2
tan
−1

√
3t
2
− 1


.
Thay biến t bởi biến x, ta rút ra kết quả I =
1
√
2
tan
−1

x
√
2
√
x
2
+ 3

+ C
19. I =
2

1
x

1 −
1
x
4


ln(x

2
+ 1) − ln x

dx (đề thi thử số 1 của Boxmath.vn)
1 −
1
x
4
=

1 −
1
x
2

1 +
1
x
2

⇒ x

1 −
1
x
4

=

1 −

1
x
2

x +
1
x

ln(1 + x
2
) − ln x = ln

1 + x
2
x

=
ln

x +
1
x

Tới đây chú ý cái đạo hàm

x +
1
x

′

= 1 −
1
x
2
Xét : I =

2
1
x

1 −
1
x
4


ln(x
2
+ 1) − ln x

dx =

2
1

x +
1
x

ln


x +
1
x

1 −
1
x
2

dx
Đặt : t = x +
1
x
⇒ dt =

1 −
1
x
2

dx
Đổi cận : x = 1 ⇒ t = 2 ; x = 2 ⇒ t =
5
2
Lúc này ta có : I =

5
2
2

t ln tdt Đặt :

u = ln t
dv = tdt
⇒





du =
1
t
v =
t
2
2
Lúc này ta có :
I =
t
2
2
ln t




5
2
2

−

5
2
2
t
2
dt =
(
5
2
)
2
2
ln
5
2
−
2
2
2
ln 2

5
2
2
t
2
dt
=

25
8
ln
5
2
−
t
2
4




5
2
2
=
25
8
ln
5
2
− 2 ln 2 −



(
5
2
)

2
4
−
2
2
4



=
25
8
ln 5 −
25
8
ln 2 − 2 ln 2 −
9
16
=
25
8
ln 5 −
9
8
ln 2 −
9
16
.
Phần 2: Tích phân
Tính các tích phân sau

1. A =

3
1

x
4 − x
dx = 8
√
3

1
√
3
t
2
(t
2
+ 1)
2
dt = −4
√
3

1
√
3
td(
1
t

2
+ 1
) = −
4t
t
2
+ 1
|
1
√
3
√
3
+ 4
√
3

1
√
3
1
t
2
+ 1
dt

t =

x
4 − x

⇒ x =
4t
2
t
2
+ 1
⇒ dx =
8t
(t
2
+ 1)
2

maxmin onluyentoan.vn
2. A =
2

1
x
4
+ 1
x
6
+ 1
dx
I =

2
1
(x

2
+ 1)
2
− 2x
2
x
6
+ 1
dx =

2
1
(x
2
+ 1)
2
(x
2
+ 1)(x
4
− x
2
+ 1)
dx−

2
1
2x
2
(x

3
)
2
+ 1
dx =

2
1
x
2
+ 1
x
4
− x
2
+ 1
dx−

2
1
2x
2
(x
3
)
2
+ 1
dx
I =


2
1

1 +
1
x
2

x
2
+
1
x
2
− 1
dx −

2
1
2x
2
(x
3
)
2
+ 1
dx
Đặt

x −

1
x

= t ⇔

1 +
1
x
2

dx = dt và x
3
= u ⇔ 3x
2
dx = du
Ta có: I =

3
2
0
1
t
2
+ 1
−
2
3

8
1

1
u
2
+ 1
du
3. Biến đổi :
3e
2x
− 5e
x
+ 4
e
x
+ 1
= 4 + 3e
x
−
12e
x
e
x
+ 1
= (4x + 3e
x
)
′
− 12 (ln (e
x
+ 1))
′

Nên: J =
1

0
3e
2x
− 5e
x
+ 4
e
x
+ 1
dx =
1

0
d (4 + 3e
x
− 12 ln (e
x
+ 1)) = (4 + 3e
x
− 12 ln (e
x
+ 1))
1
0
4. I =

1

0
x − e
2x
x.e
x
+ e
2x
dx
Ta có
I =
1

0
(x + e
x
) − e
x
(1 + e
x
)
e
x
(x + e
x
)
dx =
1

0


1
e
x
−
1 + e
x
x + e
x

dx =

−
1
e
x
− ln |x + e
x
|





1
0
= 1 −
1
e
− ln(1 + e).
5. I =


π
4
0
x. tan
2
xdx
Chú ý rằng

tan
2
xdx =


(tan
2
x + 1) − 1

dx = tan x − x + C Đặt

u = x
v = tan
2
xdx
⇒

du = d x
v = tan x − x
Từ đó ta có :I = x (tan x − x)|
π

4
0
−

π
4
0
tan xdx +

π
4
0
xdx = x (tan x − x)|
π
4
0
+ ln(cos x)|
π
4
0
+
x
2
2




π
4

0
6. I =

2
1
x
3
√
x
3
+ 8 + (3x
3
+ 5x
2
) ln x
x
dx
I =

2
1
x
3
√
x
3
+ 8 + (3x
3
+ 5x
2

) ln x
x
dx I =

2
1
x
2

x
3
+ 8 dx +

2
1
(3x
2
+ 5x) ln x dx
I =
1
3

2
1

x
3
+ 8 d(x
3
+ 8) +


2
1
ln x d

x
3
+
5
2
x
2

T =

2
1
x
2
− 1
(x
2
− x + 1)(x
2
+ 3x + 1)
dx
T =

2
1

1 −
1
x
2
(x +
1
x
− 1)(x +
1
x
+ 3)
dx
Đặt t = x +
1
x
⇒ dt = (1 −
1
x
2
)dx.
Khi x = 1 thì t = 2, khi x = 2 thì t =
5
2
Ta có: T =

5
2
2
dt
(t − 1)(t + 3)

dt =
1
4

5
2
2

1
t − 1
−
1
t + 3

dt =
1
4
.ln




t − 1
t + 3










5
2
2
7. I =
2

0
xdx
√
2 + x +
√
2 − x
Đặt t =
√
2 − x +
√
2 + x ⇒ t
2
− 4 = 2
√
4 − x
2
⇒ (t
2
− 4)
2
= 16 −4x

2
⇒ t(t
2
− 4)dt = −2xdx
Đổi cận : x = 0 ⇒ t = 2
√
2; x = 2 ⇒ t = 2
Từ đó ta có tích phân : I =
1
2
2
√
2

2
t

t
2
− 4

t
dt =
1
2
2
√
2

2


t
2
− 4

dt =
1
2

t
3
3
− 4t





2
√
2
2
=
8 − 4
√
2
3
maxmin onluyentoan.vn
—————nat—————
maxmin onluyentoan.vn