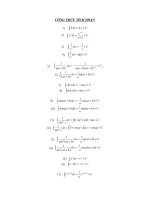CÔNG THỨC TÍCH PHÂN
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (60.43 KB, 1 trang )
______________________________________________________________NGÔ NHẬT MINH
COÂNG THÖÙC TÍCH PHAÂN
1)
∫
+=
Cxkdxk ..
2)
∫
+
+
=
+
C
n
x
dxx
n
n
1
1
3)
∫
+−=
C
x
dx
x
11
2
4)
∫
+=
Cxdx
x
ln
1
5)
∫
+
+−
−=
+
−
C
baxna
dx
bax
nn 1
))(1(
1
)(
1
; 6)
∫
++=
+
Cbax
a
dx
bax
ln
1
)(
1
7)
∫
+−=
Cxdxx cos.sin
8)
∫
+=
Cxdxx sin.cos
9)
∫
++−=+
Cbax
a
dxbax )cos(
1
)sin(
10)
∫
++=+
Cbax
a
dxbax )sin(
1
)cos(
11)
∫ ∫
+=+=
Ctgxdxxtgdx
x
).1(
cos
1
2
2
12)
( )
∫ ∫
+−=+=
Cgxdxxgdx
x
cotcot1
sin
1
2
2
13)
∫
++=
+
Cbaxtg
a
dx
bax
)(
1
)(cos
1
2
14)
∫
++−=
+
Cbaxg
a
dx
bax
)(cot
1
)(sin
1
2
15)
∫
+=
Cedxe
xx
16)
∫
+−=
−−
Cedxe
xx
17)
∫
+=
++
Ce
a
dxe
baxbax )()(
1
18)
∫
+
+
+
=+
+
C
n
bax
a
dxbax
n
n
1
)(
.
1
.)(
1
(n
≠
1)
19)
∫
+=
C
a
a
dxa
x
x
ln
20)
∫
+=
+
Carctgxdx
x 1
1
2
21)
∫
+
+
−
=
−
C
x
x
dx
x
1
1
ln
2
1
1
1
2
22)
∫
+=
+
C
a
x
arctg
a
dx
ax
11
22
23)
∫
+
+
−
=
−
C
ax
ax
a
dx
ax
ln
2
11
22
24)
∫
+=
−
Cxdx
x
arcsin
1
1
2
25)
∫
+=
−
C
a
x
dx
xa
arcsin
1
22
26)
∫
+±+=
±
Cxxdx
x
1ln
1
1
2
2
27)
∫
+±+=
±
Caxxdx
ax
22
22
ln
1
28)
∫
++−=−
C
a
xa
xa
x
dxxa arcsin
22
2
2222
29)
∫
+±+±±=±
Caxx
a
ax
x
dxax
22
2
2222
ln
22