Chủ Đề 07_ Bí Quyết Nhận Diện Đồ Thị Hàm Số.doc

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (892.71 KB, 11 trang )

Trang 1<div class="page_container" data-page="1">

CHỦ ĐỀ 7: BÍ QUYẾT NHẬN DIỆN ĐỒ THỊ HÀM SỐA. KIẾN THỨC NỀN TẢNG

1. Nhận diện đồ thị hàm bậc 3 y ax 3bx2cx d a ( 0)

Đồ thị hàm số có dạng chữ N nếu a > 0 và có dạng chữ N ngược nếu a < 0

Hàm số có 2 cực trị  y' 0 khi đó hồnh độ điểm cực trị là x1, x2 là nghiệm của phương trình' 0

 

Đồ thị hàm số cắt trục tung tại A



0;c . Nếu điểm A nằm trên trục hoành



 c0và nếu điểm A nằm

 và có tiệm cận ngang là yac

4. Nhận biết hàm chứa dấu giá trị tuyệt đối y f x

 

Ta giữ nguyên phần đồ thị phía trên trục hoành của đồ thị hàm yf x

 

và xóa phần đồ thị nằm phíadưới trục hồnh đồng thời lấy đối xứng của phần đồ thị này lên trên trục hoành

5. Nhận biết hàm chứa dấu giá trị tuyệt đối yf x

 

Ta giữ nguyên phần đồ thị phía bên phải trục tung của đồ thị hàm số yf x

 

và xóa phần đồ thị nằmphía bên trái trục tung sau đó lấy đối xứng của phần đồ thị bên phải trục tung sang bên trái trục tung.

B. VÍ DỤ MINH HỌA

Dạng 1: Tìm các hệ số của hàm số thơng qua đồ thị cho trước

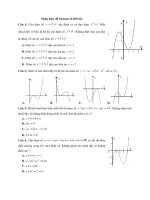
Ví dụ 1 (Đề minh họa BGD-ĐT 2018): Đường cong hình bên là đồ thị hàm số nào sau đây?A. yx42x22 B. y x 4 2x22

</div>Trang 2<div class="page_container" data-page="2">

C. 1

Đáp án D là sai vì a b  .



1 . 3

 





 3 0 vậy theo cơng thức giải nhanh nếu ab > 0 thì đồ thị hàm bậc 4

trùng phương chỉ có 1 điểm cực trị duy nhất

Ví dụ 2 (Chuyên Bắc Ninh 2018): Đường cong hình bên là đồ thị hàm số trong

Lại thấy đồ thị hàm số có 2 điểm cực trị  y ' 0 đổi dấu 2 lần  phương trình bậc 2 của ' 0y  có 2

nghiệm phân biệt.

</div>Trang 3<div class="page_container" data-page="3">

 có đồ thị như hìnhvẽ. Tính giá trị biểu thức T   a b c.

Đề bài còn cho dữ kiện đồ thị đi qua điểm B



0; 1



thay vào hàm số thì vẫn tìm được a tuy nhiên tathường chọn điểm A thì tính tốn dễ dàng hơn.

Dạng 2: Nhận dạng đồ thị chứa dấu giá trị tuyệt đối

Ví dụ 4 (Đề tham khảo Bộ GD&ĐT ): Hàm số

 

2



y x x  có đồ thị nhưhình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y x 2



x21 ?



Đặt yf x

  

 x 2





x21



và g x

 

 x 2



x21 .



Đồ thị hàm số yf x và y g x

 



 

đều cắt trụhoành tại 3 điểm phân biệt x2,x 1 Đáp số C sai

</div>Trang 4<div class="page_container" data-page="4">

Xét dấu x  2 ta đuợc 2 trường hợp

Trường hợp 1 với x2 thì x 2 0 khi đó x 2  x 2 và y x 2



x21







x 2

 

x21



có nghĩa làphần đồ thị nằm phía bên phải giá trị x 2 sẽ giữ nguyên.  Cả 4 đáp án đều đúng

Trường hợp 2 với x2 thì x 2 0 khi đó



2

  

2



Đáp án B sai vì đây là đồ thị hàm số y



x 2



x21Đáp án D sai vì đây là đồ thị hàm số y



x 2

 

x21



Dạng 3: Nhận diện đồ thị hàm số dựa vào hệ số của biến x

Ví dụ 5 (Chuyên ĐHSP Hà Nội - Lần 2 ): Cho hàm số y ax 4bx2c có đồthị như hình 10. Mệnh đề nào dưới đây đúng?

Vì đồ thị có 3 cực trị  theo cơng thức giải nhanh thì a b.  0 b 0 Cả A và D đều thỏa mãn nên tatiếp tục phải tìm thêm dấu hiệu thứ 3.

Vì đồ thị hàm số cắt trục tung tại điểmA



0;c , quan sát hình vẽ ta thấy điểm này nằm phía dưới của trục



hồnh  giá trị c < 0

=> Chọn DBình luận

Nếu đồ thị có dạng chữ W thì a > 0

Nếu điểm A



0;c nằm phía trên trục hồnh thì c > 0, điểm A nằm trên trục hồnh thì



c 0

Ví dụ 6 (Chun ĐHSP Hà Nội - Lần 2 ): Cho hàm số y ax 3bx2cx d có đồ thị như hình 4. Tìmkhẳng định đúng.

A. , 0; 0

a dbc

C. , , 0

a b dc

 

=> Chọn C

</div>Trang 5<div class="page_container" data-page="5">

Ví dụ 7 (Chuyên ĐH Vinh, lần 1): Hình 14 là đồ thị của hàm số yax b.

cx d

Mệnh đề nào sau đây đúng?

A. ad 0,ab0. B.bd 0,ab0.

C. ab0,ad 0. D. bd0,ad0.

=> Chọn A

Ví dụ 8 (chuyên Thái Bình ): Cho hàm số yf x

 

có đồ thị yf x'

 

cắt

trục Ox tại ba điểm có hồnh độ a, b, c như hình vẽ. Khẳng định nào dưới đây có

Câu 3 (Chuyên Hạ Long - 2018).

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số đượcliệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

A. y x 3 3x21 B. y2x4 4x21

C. yx33x21 D. y2x44x21

</div>Trang 6<div class="page_container" data-page="6">

Câu 4 (Chuyên Lê Hồng Phong - 2018).

A. yx3 3x21 B. y x 3 3x1

C. y x 3 3x1 D. yx33x21

Câu 5 (Chuyên Lê Hồng Phong - 2018).

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm sốđược liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàmsố nào ?

y x  B. y x 3 3x21

C. y2x3 6x2 1 D. y x3 3x21

</div>Trang 7<div class="page_container" data-page="7">

A. c b a  B. b a c 

C. c a b  D. b c a 

Câu 11 (THPT Phan Bội Châu - 2018).

Đồ thị sau đây là đồ thị của hàm số nào?

Câu 12 (THPT Phan Bội Châu - 2018).

Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?

</div>Trang 8<div class="page_container" data-page="8">

Câu 14 (Sở GD&ĐT Bà Rịa Vũng Tàu - 2018).

Đường cong hình bên (Hình 1) là đồ thị của một hàm số trong bốn hàm sốđược liệt kê trong bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm sốnào?

A. yx33x2 B. y x 34x 5

C. y x 3 3x2 D. yx3 3x2

Câu 15 (THPT Hai Bà Trưng - 2018).

Cho hàm số y x 3 6x29xcó đồ thị như Hình 1.Khi đó đồ thị Hình 2 là của hàm số nào dưới đây?

Câu 16 (THPT TH Cao Nguyên - 2018).

Cho đồ thị hàm số yf x

 

như hình vẽ bên. Đồ thị trong phương ánnào sau đây là đồ thị hàm số y f x

 

</div>Trang 9<div class="page_container" data-page="9">

Hình nào dưới đây là đồ thị của hàm



2



1 ?2

yx x 

Câu 18 (Sở GD-ĐT Bình Phước - 2018).

Tìm a, b, c để hàm số yax 2cx b



</div>Trang 10<div class="page_container" data-page="10">

Câu 22 (Đề minh họa - 2018).

Câu 23 (Chuyên Thái Bình - 2018).

Cho hàm số yf x

 

có đồ thị yf x'

 

cắt trục Ox tại ba điểm có hồnhđộ a b c  như hình vẽ. Mệnh đề nào dưới đây là đúng?

A. f c

 

 f a

 

 f b

 

B. f c

 

 f b

 

 f a

 

C. f a

 

 f b

 

 f c

 

D. f b

 

 f a

 

 f c

 

Câu 24 (Chuyên Lê Hồng Phong - 2018).

Cho 3 hàm số yf x

 

, y g x

 

 'f x

 

, y h x

 

g x'

 

có đồ thị là 3đường cong trong hình vẽ bên. Mệnh đề nào sau đây đúng?

A. g



1



h



1



 f



1



B. h



1



g



1



 f



1



C. h



1



 f



1



g



1



D. f



1



g



1



h



1



Câu 25 (Chuyên Lê Hồng Phong - 2018).

Cho 3 hàm số yf x

 

, y g x

 

 'f x

 

, y h x

 

g x'

 

có đồ thị là 3đường cong trong hình vẽ bên. Mệnh đề nào sau đây đúng?

A. g



1



h



1



 f



1



B. h



1



g



1



 f



1



C. h



1



 f



1



g



1



D. f



1



g



1



h



1



Câu 26 (THPT Chu Văn An - 2018).

Cho hàm số yf x

 

liên tục và có đạo hàm cấp hai trên R. Đồ thị của cáchàm số yf x y

 

, f x và( ) yf( )x lần lượt là các đường cong nàotrong hình vẽ bên?

</div>Trang 11<div class="page_container" data-page="11">

A. yln|x  1 ln 2| B. yln x

C. yln



x1



 ln 2 D. ylnx

Câu 29 (THPT Chuyên ĐH Vinh – Lần 4 - 2018).

Cho các số thực a, b khác 1. Biết rằng bất kỳ đường thẳng nào songsong với trục Ox mà cắt các đường y a y b x,  x, trục tung lần lượt tại

M, N và A thì AN 2AM (hình vẽ bên). Mệnh đề nào sau đây đúng?

</div>