BÀI TẬP MẶT CẦU MỚI VÀ HOT NHẤT

BÀI TẬP VỀ MẶT CẦU
Lớp 12B
4
* Chứng minh các điểm thuộc mặt cầu, xác đònh tâm và bán kính mặt cầu.
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và SA
⊥
(ABC).
a) Gọi O là trung điểm SC. Chứng minh: OA = OB = OC = OS. Suy ra bốn điểm A, B, C, S
cùng nằm trên mặt cầu tâm O bán kính r =
2
1
SC.
b) Cho SA = BC = a và AB = a
2
. Tính bán kính mặt cầu nói trên.
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA
⊥
(ABCD) và SA = a
3
.
Gọi O là tâm ABCD và K là hình chiếu của B trên SC.
a) Chứng minh 3 điểm O, A, K cùng nhìn đoạn SB dưới một góc vuông. Suy ra năm điểm
S, O, A, K, B cùng nằm trên mặt cầu đường kính SB.
b) Xác đònh tâm và tính bán kính mặt cầu trên.
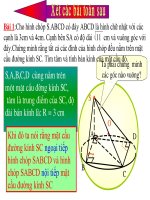
Bài 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên đều bằng a. Xác đònh tâm
và tính bán kính của mặt cầu đi qua năm điểm S, A, B, C, D.
Bài 4: Chứng minh 8 đỉnh của một hình hộp chữ nhật cùng nằm trên một mặt cầu. Tính bán kính
của mặt cầu ấy, biết hình hộp chữ nhật có ba kích thước là a, b, c.
Bài 5: Tìm tập hợp các điểm M sao cho tổng bình phương khoảng cách từ M đến hai điểm A, B
cố đònh bằng một hằng số k
2

.
Bài 6: Cho hai điểm A, B cố đònh. Chứng minh rằng tập hợp các điểm M trong không gian sao
cho
.MA
MB
= 0 là mặt cầu đường kính AB.
Bài 7: Cho tứ diện đều ABCD cạnh a. Tìm tập hợp các điểm M trong không gian sao cho:
MA
2
+ MB
2
+ MC
2
+ MD
2
= 2a
2
.
* Vò trí tương đối của mặt cầu với mp và đường thẳng.
Bài 8: Xác đònh thiết diện tạo bởi mp (P) với mặt cầu S(O; R) biết khoảng cách từ O đến (P) là
2
R
Bài 9: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Hãy xác đònh tâm và bán kính của mặt cầu
tiếp xúc với 6 mặt của hình lập phương.
Bài 10: Cho mặt cầu S(O; a) và một điểm A, biết OA = 2a, qua A kẻ một tiếp tuyến tiếp xúc với
(S) tại B và cũng qua A kẻ một cát tuyến cắt (S) tại C và D, biết CD = a
3
.
a) Tính AB.
b) Tính khoảng cách từ O đến đường thẳng CD.

Bài 11: Cho tam giác ABC có độ dài ba cạnh là 13, 14, 15. Một mặt cầu tâm O, bán kính R = 5
tiếp xúc với ba cạnh của tam giác ABC tại các tiếp điểm nằm trên ba cạnh đó. Tính khoảng cách
từ tâm mặt cầu tới mp chứa tam giác.
Bài 12: Cho hình chóp S.ABC. Biết rằng có một mặt cầu bán kính R tiếp xúc với các cạnh của
hình chóp và tâm I của mặt cầu nằm trên đường cao SH của hình chóp.
a) Chứng minh rằng S.ABC là hình chóp đều.
b) Tính đường cao của hình chóp, biết rằng IS = R
3
.
* Diện tích mặt cầu và thể tích khối cầu.
Bài 13: Cho một tứ diện đều ABCD có cạnh a.
a) Xác đònh tâm và bán kính mặt cầu ngoại tiếp tứ diện.
b) Tính diện tích mặt cầu.
c) Tính thể tích khối cầu tương ứng.
Bài 14: Cho một hình chóp tứ giác đều có cạnh đáy là a, cạnh bên hợp với đáy một góc 60
o
.
a) Xác đònh tâm và bán kính mặt cầu ngoại tiếp hình chóp.
b) Tính diện tích mặt cầu.
c) Tính thể tích khối cầu tương ứng.
* Mặt cầu ngoại tiếp hình chóp
Bài 15: Tính bán kính mặt cầu ngoại tiếp một hình chóp tam giác đều có cạnh đáy bằng a và
cạnh bên bằng b.
Bài 16: Hình chóp S.ABC có đường cao SA = a, đáy ABC là tam giác đều cạnh a. Tính bán kính
mặt cầu ngoại tiếp hình chóp.
Bài 17: Cho hình chóp tam giác đều S.ABC, có cạnh đáy là a và góc hợp bởi mặt bên và đáy
bằng 60
o
. Gọi O là tâm của tam giác ABC. Trong tam giác SAO dựng đường trung trực của cạnh
SA cắt SO tại K.

a) Tính SO, SA.
b) Chứng minh
SMK∆
đồng dạng với
SOA∆
(M là trung điểm SA). Suy ra KS.
c) Chứng minh hình chóp K.ABC là hình chóp đều. Suy ra: KA = KB = KC.
d) Xác đònh tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
Bài 18: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc hợp bởi mặt bên và đáy
bằng 60
o
. Xác đònh tâm và tính bán kính mặt cầu ngoại tiếp hình chóp.
Bài 19: Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Chứng minh rằng hình
chóp đó có mặt cầu ngoại tiếp. Xác đònh tâm và tính bán kính của mặt cầu đó.