bài giảng về ứng dụng tin học trong thiết kế thí nghiệm và xử lý số liệu

TRƯỜNG ĐẠI HỌC NÔNG LÂM HUẾ
DỰ ÁN HỢP TÁC VIỆT NAM – HÀ LAN





BÀI GIẢNG
NGHIÊN CỨU CHUYÊN SÂU














Người biên soạn: PGS.TS Nguyễn Minh Hiếu

Huế, 08/2009

TRƯỜNG ĐẠI HỌC NÔNG LÂM
DỰ ÁN GIÁO DỤC VIỆT NAM HÀ LAN




BÀI GIẢNG
ỨNG DỤNG TIN HỌC TRONG
THIẾT KẾ THÍ NGHIỆM VÀ XỬ LÝ SỐ LIỆU
(Phương pháp nghiên cứu nâng cao)



LÊ ĐÌNH PHÙNG
NGUYỄN MINH HIẾU

HUẾ, 2008

2

MỤC LỤC
MỞ ĐẦU 2
BÀI I: NHẬP SỐ LIỆU 4
1.1. Nguyên tắc của nhập số liệu 4
1.2. Nhập số liệu trong trường hợp số liệu không phân nhóm/tổ 4
1.3. Nhập số liệu trong trường hợp số liệu phân tổ bởi một nhân tố 5
1.4. Nhập số liệu trong trường hợp số liệu phân tổ bởi hai nhân tố 6
1.5. Nhập số liệu trong các kiểu thiết kế thí nghiệm có sự khống chế sự sai khác ban đầu
7
BÀI 2. KIỂM TRA SỐ LIỆU VÀ ĐỊNH HƯỚNG PHÂN TÍCH 10
2.1. Kiểm tra số liệu bằng trình ứng dụng filter trong EXCEL 11
2.2. Kiểm tra số liệu bằng trình ứng dụng Box-plot hoặc Scatter Plot trong SPSS 14
BÀI 3. PHÂN TÍCH THỐNG KÊ MÔ TẢ 19
3.1. Phân tích thống kê mô tả trong trường hợp tập hợp số liệu không phân nhóm 20
3.2. Phân tích thống kê mô tả trong trường hợp tập hợp số liệu phân nhóm 21
BÀI 4. PHÂN TÍCH PHƯƠNG SAI 23
BÀI 5. PHÂN TÍCH PHƯƠNG SAI CHO CÁC KIỂU THIẾT KẾ THÍ NGHIỆM
KHÁC NHAU 28
5.1. Nguyên tắc của phân tích số liệu của thiết kế thí nghiệm RCB và LSD 28
5.2. Phân tích số liệu từ thí nghiệm kiểu RCB 29
5.3. Phân tích số liệu từ thí nghiệm kiểu LSD 34
BÀI 6. ÁP DỤNG QUY TẮC NGẪU NHIÊN TRONG THIẾT KẾ THÍ NGHIỆM VỚI
MỘT NHÂN TỐ 39
6.1. Ngẫu nhiên hóa trong thiết kế thí nghiệm kiểu CRD và RCB 39

6.2. Ngẫu nhiên hóa trong thiết kế thí nghiệm kiểu LSD 41
BÀI 7. PHÂN TÍCH HỒI QUY 42





















3

MỞ ĐẦU
Hai giai đoạn thú vị nhất trong nghiên cứu là thiết kế thí nghiệm và xử lý số
liệu. Tuy nhiên, đây là hai giai đoạn tiêu tốn thời gian nhất. Trong một thí nghiệm, quá
trình thiết kế thí nghiệm và xử lý số liệu không phải chỉ tiến hành một lần mà thường
được lặp đi lặp lại nhiều lần, đặc biệt là giai đoạn xử lý số liệu. Nhận định này càng

đúng khi làm việc với một tập hợp số liệu lớn, ví dụ số liệu điều tra. Hiểu bản chất của
thiết kế thí nghiệm và xử lý số liệu là đặc biệt quan trọng. Quá trình thiết kế thí nghiệm
và xử lý số liệu sẽ nhanh hơn, chính xác hơn và thú vị hơn nếu chúng ta có thể ứng
dụng tin học vào phân tích số liệu thay vì tính toán đơn thuần.
Hiện nay có rất nhiều phần mềm giúp cho quá trình xử lý số liệu. Nếu chúng ta
sử dụng các phần mềm để phân tích kết quả thì luôn luôn có kết quả. Vấn đề cơ bản là
kết quả đó đúng hay sai, kết quả đó nói lên điều gì. Quả là không thừa khi nhấn mạnh
rằng chúng ta phải hiểu được bản chất của thiết kế thí nghiệm và xử lý số liệu trước khi
ứng dụng công nghệ thông tin. Tất cả các kiến thức về bản chất của thiết kế thí nghiệm
và xử lý số liệu được đề cập trong học phần phương pháp thí nghiệm. Trong phạm vi
của học phần này chúng tôi đề cập đến việc vận dụng phầm mềm SPSS trong xử lý số
liệu.
Phầm mềm SPSS là một phần mềm rất thông dụng. Chúng ta có thể có được
phầm mềm này bất kỳ ở đâu. Việc xử dụng phần mềm này rất đơn giản, nhưng lại rất
có hiệu quả. Có thể nói rằng phần mềm SPSS giải quyết được gần như toàn bộ các yêu
cầu của xử lý số liệu trong các nghiên cứu trong nông nghiệp. Mặt khác phần mềm
SPSS cũng có ưu thế xử lý các tập hợp số liệu khá lớn như số liệu điều tra. Do vậy,
chúng ta có thể hoàn toàn sử dụng phần mềm SPSS cho xử lý số liệu thí nghiệm và số
liệu điều tra. Một ưu điểm khác nữa là kết quả đầu ra của xử lý số liệu bằng phần mềm
SPSS có thể được thao tác và chế bản một cách dễ dàng trên các phần mềm khác như
Microsoft Offices. Điều này rất thuận lợi khi chúng ta sử dụng kết quả xử lý số liệu cho
việc hoàn thành bài báo hay luận văn. Hơn thế nữa cách sử dụng phầm mềm SPSS
cũng tương tự như một số phầm mềm thông dụng khác như GENSTAT, MINITAB,
vv. Do vậy, quả là khiêm tốn để nói rằng nếu chúng ta có thể sử dụng được phần mềm
SPSS thì chúng ta có thể sử dụng các phần mềm tin học thống kê khác.
Với mục đích giúp cho đối tượng học bậc đại học có thể sử dụng phần mềm
SPSS trong xử lý số liệu nghiên cứu, chúng tôi biên soạn nội dung học phần này và
khi kết thúc chương này, hy vọng người đọc có thể thực hiện một số nội dung sau bằng
phần mềm SPSS:
 Nhập số liệu cho các loại thiết kế thí nghiệm khác nhau

 Kiểm tra được số liệu và định hướng phân tích
 Phân tích thống kê mô tả
 Phân tích phương sai
 Xử lý số liệu thí nghiệm một nhân tố

4

 Áp dụng quy tắc ngẫu nhiên trong thiết kế thí nghiệm
 Phân tích tương quan hồi quy

BÀI I: NHẬP SỐ LIỆU
Mấu chốt của xử lý số liệu bằng các phầm mềm tin học là nhập số liệu theo cách
máy có thể hiểu được. Máy tính sẽ xử lý đúng nếu ta nhập số liệu đúng. Nhập và quản
lý số liệu là một công đoạn quan trọng trong quá trình nghiên cứu. Cách thức nhập và
quản lý số liệu đòi hỏi phải dễ hiễu đối với các thành viên trong và ngoài nhóm nghiên
cứu. Hơn thể nữa, nhập và quản lý số liệu phải thuận lợi cho quá trình xử lý số liệu sau
này. Để nhập số liệu chúng ta có thể có hai lựa chọn. Nhập số liệu trong phần mềm
EXCEL sau đó mỗi khi xử lý số liệu thì nạp (import) số liệu vào phần mềm SPSS. Lựa
chọn thứ 2 là nhập số liệu trực tiếp vào phần mềm SPSS. Mỗi cách nhập có những ưu
điểm và nhược điểm của nó. Trong phạm vi của chương này chúng tôi giới thiệu sự lựa
chọn thứ nhất, nhập và quản lý số liệu từ EXCEL.
1.1. Nguyên tắc của nhập số liệu
Để có thể nhập số liệu chúng ta cần xác định rõ:
 Đơn vị thí nghiệm của nghiên cứu
 Số biến độc lập của nghiên cứu
 Số biến phụ thuộc của nghiên cứu
Để nhập số liệu đúng, cần tuyệt đối tuân theo các nguyên tắc sau đây:
 Mỗi đơn vị thí nghiệm được nhập vào trong một hàng của worksheet
excel. Tất cả các thông tin của mỗi đơn vị thí nghiệm phải đều được nằm
cùng trong một hàng.

 Hàng thứ nhất của worksheet excel là hàng tên biến (độc lập và phụ
thuộc).
 Mỗi biến độc lập hay biến phụ thuộc nằm trong một cột. Tất cả các thông
tin về một biến phải được nằm trong một cột.
Ngoài ra để mọi người đều có thể hiểu được tập hợp số liệu, nên dùng các chức
năng phụ trợ khác trong excel để giải thích thêm về tập hợp số liệu. Ví dụ ta có thể
dùng chức năng insert comment để chú thích các tên biến, đơn vị của biến cũng như
chú thích các số liệu cần thiết.

1.2. Nhập số liệu trong trường hợp số liệu không phân nhóm/tổ
Ví dụ 1. Một nhóm nghiên cứu đã tiến hành xác định năng suất lúa (kg/ha) tại
10 ô ruộng, kết quả thu được ở bảng 1. Hãy nhập số liệu để phân tích thống kê mô tả
năng suất lúa.

5

Bảng 1. Năng suất lúa (kg/ha) ở 10 ô ruộng khác nhau
STT Năng suất
(kg/ha)
STT

Năng suất
(kg/ha)
1 3.853 6 2.606
2 4.788 7 4.936
3 4.576 8 4.454
4 6.034 9 5.276
5 5.874 10 5.916

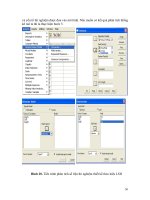
Chúng ta có thể nhập số liệu như sau:

Hình 1: Nhập số liệu trong trường hợp số liệu không phân tổ

1.3. Nhập số liệu trong trường hợp số liệu phân tổ bởi một nhân tố
Ví dụ 2. Một nhóm nghiên cứu đã tiến hành nghiên cứu ảnh hưởng của các mức
phân bón đến năng suất lúa (kg/ha) trong một thí nghiệm được thiết kế theo kiểu CRD,
kết quả thu được ở bảng 2. Hảy nhập số liệu để phân tích ảnh hưởng của các mức phân
bón đến năng suất lúa.

6

Bảng 2. Số liệu từ thí nghiệm ảnh hưởng của mức phân bón đến năng suất lúa
(kg/ha)
Công thức phân bón Lặp lần 1 Lặp lần 2 Lặp lần 3 Lặp lần 4
N
0
3.853 2.606 3.144 2.894
N
1
4.788 4.936 4.562 4.608
N
2
4.576 4.454 4.884 3.924
N
3
6.034 5.276 5.906 5.652
N
4
5.874 5.916 5.984 5.518
Chúng ta có thể nhập số liệu như sau:

Hình 2: Nhập số liệu trong trường hợp số liệu phân tổ bởi một nhân tố
1.4. Nhập số liệu trong trường hợp số liệu phân tổ bởi hai nhân tố
Ví dụ 3. Một nhóm nghiên cứu đã tiến hành nghiên cứu ảnh hưởng của các mức
đạm bón và giống lúa đến năng suất lúa (kg/ha) trong một thí nghiệm được thiết kế
theo kiểu CRD, kết quả thu được ở bảng 3. Hảy nhập số liệu để phân tích ảnh hưởng
của các mức phân bón và giống lúa đến năng suất lúa.

7

Bảng 3. Số liệu thu được từ thí nghiệm ảnh hưởng của mức đạm bón và giống
lúa đến năng suất lúa (kg/ha) trong thí nghiệm thiết kế theo kiểu CRD
Giống

Phân bón

Giống 1
(V1)
Giống 2
(V2)
Giống 3
(V3)
Giống 4
(V4)
N
0
3.853 2.606 3.144 2.894
N
1
4.788 4.936 4.562 4.608

N
2
4.576 4.454 4.884 3.924
N
3
6.034 5.276 5.906 5.652
N
4
5.874 5.916 5.984 5.518
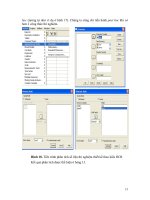
Có thể nhập số liệu như sau:

Hình 3: Nhập số liệu trong trường hợp số liệu phân tổ bởi hai nhân tố
1.5. Nhập số liệu trong các kiểu thiết kế thí nghiệ m có sự khống chế sự sai khác
ban đầu
Ví dụ 4. Một nhóm nghiên cứu đã tiến hành nghiên cứu ảnh hưởng của các mức
đạm bón và giống lúa đến năng suất lúa (kg/ha) trong một thí nghiệm được thiết kế
theo kiểu RCB, kết quả thu được ở bảng 4. Hãy nhập số liệu để phân tích ảnh hưởng
của các mức đạm bón và giống đến năng suất lúa.

8

Bảng 4. Số liệu từ thí nghiệm ảnh hưởng của mức phân bón và giống lúa đến
năng suất lúa (kg/ha) trong thí nghiệm thiết kế theo kiểu RCB
Phân bón Giống V1
N
0
3,853 2,606 3,144 2,894
N
1
4,788 4,936 4,562 4,608

N
2
4,576 4,454 4,884 3,924
N
3
6,034 5,276 5,906 5,652
N
4
5,874 5,916 5,984 5,518

Giống V
2

N
0
2,846 3,794 4,108 3,444
N
1
4,956 5,128 4,150 4,991
N
2
5,928 5,698 5,810 4,308
N
3
5,664 5,362 6,458 5,474
N
4
5,458 5,546 5,786 5,932

Giống V

3,

N
0
4,192 3,754 3,738 3,428
N
1
5,251 4,582 4,896 4,286
N
2
5,822 4,848 5,678 4,932
N
3
5,888 5,524 6,042 4,756
N
4
5,864 6,264 6,056 5,362

Đây là một thí nghiệm hai nhân tố: giống và mức phân bón. Thí nghiệm này
được thiết kế theo kiểu RCB. Như vậy, xuất hiện thêm một yếu tố thứ 3, đó là yếu tố
khối, dùng để khống chế sự sai khác ban đầu của các đơn vị thí nghiệm. Nếu có thể
nhập số liệu của kiểu thiết kế thí nghiệm này, thì chúng ta sẽ có thể nhập được số liệu
trong các kiểu thiết kế thí nghiệm khác như LS, SPLIT-PLOT và STRIP-PLOT. Trong
phạm vi của chương trình đào tạo bậc đại học chúng tôi chỉ giới thiệu cách nhập số liệu
của hai kiểu thiết kế thí nghiệm RCB và LS.
Nguyên tắc cơ bản nhập số liệu trong các kiểu thiết kế thí nghiệm có sự khống
chế sự sai khác ban đầu (RCB, LS, SPLIT-PLOT và STRIP-PLOT) là xem xét yếu tố
khống chế như là một yếu tố thí nghiệm. Có nghĩa là mỗi một yếu tố khống chế sự sai
khác cần một cột trong worksheet của excel.
Chúng ta có thể nhập số liệu cho ví dụ 4 ở hình 4. Hình 4 trình bày cách nhập số

liệu của 14 đơn vị thí nghiệm đầu.

9



Hình 4: Nhập số liệu trong trường hợp số liệu phân tổ bởi hai nhân tố theo kiểu
thiết kế RCB
Ví dụ 5. Một nhóm nghiên cứu đã tiến hành nghiên cứu năng suất (tấn/ha) của 3
giống ngô lai A, B, D và giống đối chứng C, trong một thiết kế thí nghiệm kiểu LS,
kết quả thu được ở bảng 5. Hãy nhập số liệu để so sánh năng suất của các giống ngô.
Bảng 5. Năng suất (tấn/ha) của các giống ngô A, B, D và C trong thí nghiệm
thiết kế theo kiểu LS
Năng suất hạt (tấn/ha)
Số hàng
Cột 1 Cột 2 Cột 3 Cột 4

10

1 1,640(B) 1,210(D) 1,425(C) 1,345(A)
2 1,457(C) 1,185(A) 1,400(D) 1,290(B)
3 1,670(A) 0,710(C) 1,665(B) 1,180(D)
4 1,565(D) 1,290(B) 1,655(A) 0,660(C)

Chúng ta có thể nhập như sau (hình 5).

Hình 5: Nhập số liệu trong trường hợp thiết kế thí nghiệm kiểu LS
Tóm lại, nguyên tắc cơ bản của nhập số liệu để xử lý số liệu bằng phần mềm
SPSS cũng như các phần mềm khác như GENSTAT và MINITAB là “mỗi đơn vị thí
nghiệm nằm trong một hàng, mỗi biến nằm trong một cột”.

BÀI 2. KIỂM TRA SỐ LIỆU VÀ ĐỊNH HƯỚNG PHÂN TÍCH
Phân tích số liệu là việc làm rất đơn giản và nhanh chóng, do vậy chúng ta
không cần thiết vội vàng phân tích số liệu. Với các yêu cầu của một thí nghiệm thông

11

thường trong nông nghiệp, phân tích số liệu có thể hoàn thành trong vài phút. Tuy
nhiên, nếu không kiểm tra số liệu một cách cẩn thận thì việc xử lý số liệu có thể phải
làm đi làm lại nhiều lần do sau khi hoàn thành xử lý số liệu, nhà nghiên cứu có thể phát
hiện một số số liệu chưa được nhập chính xác. Tập hợp số liệu càng lớn bao nhiêu thì
việc kiểm tra số liệu càng quan trọng bấy nhiêu.
Mục đích cơ bản của việc kiểm tra số liệu là phát hiện ra các sai sót trong nhập
số liệu và phát hiện các trường hợp ngoại lệ (outliner). Ngoài ra việc kiểm tra số liệu
còn có thể giúp người nghiên cứu định hình được khuynh hướng của mối quan hệ giữa
các biến nghiên cứu, từ đó lựa chọn phương án phân tích số liệu thích hợp.
Việc kiểm tra số liệu có thể được thực hiện bằng nhiều cách khác nhau. Ví dụ sử
dụng trình ứng dụng filter trong EXCEL, Box plot hoặc Scatter plot trong SPSS.
2.1. Kiểm tra số liệu bằng trình ứng dụng filter trong EXCEL
Kiểm tra số liệu bằng cách sử dụng trình ứng dụng filter (lọc) có thể được thực
hiện một cách dễ dàng và nhanh chóng, đặc biệt khi chúng ta có tập hợp số liệu nhỏ.
Ví dụ 6. Hãy kiểm tra các số liệu đã nhập ở bảng 2 (ví dụ 2). Cần chú ý rằng
đây là một tập hợp số liệu rất đơn giản chúng ta hoàn toàn có thể kiểm tra bằng mắt
thường. Tuy nhiên từ các ví dụ đơn giản chúng ta cần khái quát hóa thành phương pháp
kiểm tra số liệu cho mọi tập hợp số liệu khác nhau.
Chúng ta có thể kiểm tra như sau:
 Bước 1: Khởi động chức năng filter. Việc khởi động này có thể thực hiện
như sau: Data-Filter-AutoFilter
 Bước 2: Filter số liệu năng suất để phát hiện ra các trường hợp nhập sai
hoặc các trường hợp ngoại lệ

 Bước 3: Chọn số liệu được cho là sai hoặc ngoại lệ để phát hiện bản ghi
(đơn vị thí nghiệm) nào chứa số liệu đó
Từ hình 6 không có sai sót nào được phát hiện trong nhập số liệu. Giả sử chúng
ta đã nhập sai số liệu của đơn vị thí nghiệm thứ nhất, thay vì nhập 3.853 chúng ta đã
nhập thành 38.533. Từ hình 7, chúng ta có thể đặt nghi ngờ về độ chính xác của bản
ghi có năng suất 38.533.

12


Hình 6. Kiểm tra số liệu bằng chức năng Filter
Như vậy nếu nhìn vào hình 7 thì chúng ta có thể phát hiện bản ghi (đơn vị thí
nghiệm) có năng suất 38.533. Chúng ta có thể di chuyển thẳng đến đơn vị thí nghiệm
có chứa số liệu 38.533. Khi đó các đơn vị thí nghiệm khác sẽ bị ẩn (8). Màu sắc của
filter bị thay đổi. Sự thay đổi màu sắc này báo hiệu tập hợp số liệu nghiên cứu đang bị
filter (lọc). Nếu chúng ta muốn thao tác với toàn bộ số liệu thì chú ý phải bỏ chức năng
filter. Điều này có thể thực hiện được bằng cách chọn ALL trong filter. Chức năng
filter còn có thể giúp ta lựa chọn được các số liệu theo một số tiêu chí nào đó do chúng
ta định ra.


13


Hình 7. Kiểm tra số liệu bằng chức năng Filter


Hình 8. Kiểm tra số liệu bằng chức năng Filter

14

2.2. Kiểm tra số liệu bằng trình ứng dụng Box-plot hoặc Scatter Plot trong SPSS
3.2.1. Nạp số liệu từ EXCEL vào SPSS
Sau khi đã nhập xong số liệu thì chúng ta có thể nạp số liệu vào SPSS để kiểm
tra số liệu cũng như phân tích và xử lý số liệu. Việc nạp số liệu vào SPSS hoàn toàn
đơn giản như việc mở một file số liệu. Chúng ta có thể tiến hành theo các bước sau
đây:
 Bước 1: Khởi động SPSS
 Bước 2: Chọn file – Open Data (hình 9)

Hình 9. Nạp số liệu vào SPSS
 Bước 3: Tìm đến file excel chứa số liệu đã nhập và mở file (open). Chú
ý: chỉ rõ loại file mà chúng ta muốn mở là file có đuôi XLS (file EXCEL). Khi muốn
nạp số liệu từ file EXCEL vào SPSS, chúng ta phải tắt file EXCEL chứa số liệu.
Ví dụ 9. Hãy nạp (input) số liệu ở ví dụ 2 từ EXCEL vào SPSS
Sau khi nạp số liệu chúng ta sẽ có kết quả như ở hình 10



15





Hình 10. Nạp số liệu vào SPSS và kết quả nạp số liệu

2.2.2. Kiểm tra số liệu bằng trình ứng dụng Box-plot hoặc Scatter- Plot trong SPSS
Thực chất của kiểm tra số liệu bằng trình ứng dụng Box-plot hoặc Scatter- Plot
trong SPSS là vẽ đồ thị Box-Plot hoặc vẽ đồ thị Scatter - Plot. Như vậy, nếu chúng ta

có thể kiểm tra số liệu bằng cách sử dụng hai loại đồ thị trên thì chúng ta cũng có thể
vẽ các đồ thị khác theo ý muốn. Thực chất là chúng ta lợi dụng chức năng vẽ đồ thị để
kiểm tra số liệu. Chúng tôi hy vọng rằng qua phần này người đọc có thể vẽ được các
loại đồ thị bằng phần mềm SPSS và kiểm tra số liệu.
Ví dụ 10. Hãy kiểm tra số liệu bằng đồ thị Box-plot trong SPSS bằng cách dùng
tập hợp số liệu ở ví dụ 2 (bảng 2.).
Chúng ta có thể làm theo các bước sau:
 Bước 1: Nạp số liệu vào SPSS
 Bước 2: Chọn Graph-Boxplot-Sinple (có thể chọn clustered trong trường
hợp số liệu phân nhóm)
 Bước 3: Chọn biến ở trục tung và biến ở trục hoành
 Bước 4: Xem xét các trường hợp ngoại lệ từ đồ thị Box-plot

16


Hình 11. Đồ thị Box-Plot mô tả mối quan hệ giữa công thức phân bón và năng
suất của lúa
Qua đồ thị trên ta không thấy những giá trị ngoại lệ. Có thể hiểu một cách đơn
giản là các giá trị nằm ngoài các đuôi của đồ thị Box-Plot thì nên được xem xét về tính
chính xác cũng như có thể được xem xét như các trường hợp ngoại lệ.
Ví dụ 11. Một nhóm nghiên cứu điều tra ảnh hưởng của tuổi của chủ hộ đến
việc chấp nhận (Y) hay không chấp nhận (N) trồng giống ngô địa phương. Kết quả
được thể hiện ở bảng 6. Hãy kiểm tra kết quả nhập số liệu.
Bảng 6. Số liệu về ảnh hưởng của tuổi chủ hộ đến chấp nhận giống ngô địa
phương
Loại hộ

Tuổi chủ hộ Tuổi chủ hộ Tuổi chủ hộ Tuổi chủ hộ
Tuổi chủ hộ

N

48

24

36

12

10

N

17

36

48

36

6

Y

46

60

5

36

14

N

24

36

24

32

92

N

17

48

36

12

12

N

17

14

24

24

2

Y

24

36

60

5

8

Y

48

36

7,5

24

8

Y

168

5

4

24

5

N0

N1

N2

N3

N4

C
ô

ng th
ứ
c ph
â
n b
ón

2500

3000

3500

4000

4500

5000

5500

6000

6500

N
ă
ng su
ấ
t

17

Y

40

30

60

36

36

N

6

5

48

24

8

Y

16

36

48

34

144

N

12

8

8

22

30

N

28

12

5

19

10

Y

46

12

72

36

7

Y

36

26

72

12

24

N

17

6

10

24

14

N

36

24

12

18

1

N

24

15

12

18

20

N

24

24

36

25

12

N

12

6

48

8

2

N

36

12

24

10

12

N

29

14

18

42

48

N

36

14

5

4

48

N

48

36

36

6

48

N

36

24

36

9

2

Y

48

24

36

60

30

N

36

24

36

46

12

N

12

12

60

24

12

N

84

6

8

32

15

N

9

36

7

92

10

Y

18

36

26

7

7

N

36

48

36

7

72

Y

60

24

22

7

30

N

15

36

18

8

60


Vẽ đồ thị kiểu Box-Plot, kết quả được trình bày ở hình 12.
Qua hình 12. có thể đặt nghi ngờ vào một số bản ghi hay đơn vị thí nghiệm thứ 9, 212,
58, 79, 76, 204, 64, 191 và 30 trong file số liệu. Các số liệu đó có thể do sai sót khi
nhập số liệu, cũng có thể là những trường hợp ngoại lệ, do vậy chúng ta cần kiểm tra
lại những số liệu này. Cần đặc biệt chú ý là không được loại bỏ các số liệu này khi
không có lý do chính đáng. Các trường hợp ngoại lệ thông thường làm cơ sở cho việc
đề xuất ý tưởng nghiên cứu mới.
Chúng ta có thể vừa kiểm tra số liệu vừa xem xét khuynh hướng của
phân bố số liệu hay xem xét mối quan hệ giữa các biến. Điều này có thể được thực hiện
thông qua đồ thị kiểu Scatter-Plot. Tiến trình vẽ đồ thị kiểu Scatter-Plot tuân theo các
bước như sau : Graphs - Scatter- Simple. Sau đó chọn biến x và biến y. Chỉ chọn
Simple khi ta muốn vẽ đồ thị đơn chỉ gồm một biến x và một biến y (Hình 13).

18


Hình 12. Đồ thị Box-Plot để kiểm tra số liệu



Hình 13. Các bước vẽ đồ thị Scatter-Plot
Hình 14 trình bày một ví dụ về đồ thị Scatter-Plot từ một tập hợp số liệu với 573
đơn vị thí nghiệm. Do tập hợp số liệu khá lớn cho nên chúng tôi không trình bày tập
hợp số liệu.
N Y
loaiho
0
50
100
150
200
t
u
o
i
58
64
30
204
191
79 76
9
212

19

Qua hình 14 ta có thể vừa kiểm tra số liệu vừa suy đoán mối quan hệ giữa các
biến. Chúng ta có thể hoàn toàn nghi ngờ bản ghi/đơn vị thí nghiệm ở hàng 262 và 481
của file nhập số liệu là những trường hợp ngoại lệ, hoặc có thể chúng đã được nhập sai.
0 20 40 60 80 100 120 140
x
50
100
150
200
250
y1
262
481

Hình 14. Đồ thị Scatter-Plot biểu thị mối quan hệ giữa biến độc lập x và biến
phụ thuộc y
Mặt khác qua hình 14 ta thấy rằng khi x nhỏ thì khi x tăng thì y tăng, nhưng khi
tiếp tục tăng x thì y sẽ không tăng nữa. Như vậy khi xem xét mối quan hệ giữa y và x
chúng ta không thể dùng một hàm tuyến tính đơn thuần được.
Tóm lại, có nhiều cách khác nhau để kiểm tra số liệu đồng thời định hình mối
quan hệ giữa các biến nghiên cứu. Người làm nghiên cứu cần chú ý đến kiểm tra số
liệu thật kỹ trước khi phân tích số liệu.

BÀI 3. PHÂN TÍCH THỐNG KÊ MÔ TẢ
Trong các chương trước chúng ta đã biết một trong những nội dung quan trọng
nhất của thống kê mô tả là tính toán các tham số đặc trưng cho mức độ tập trung như
trung bình, trung vị, và yếu số và các tham số đặc trưng cho mức độ phân tán như

phương sai, độ lệch chuẩn, sai số chuẩn của số trung bình (sai số của số trung bình).
Trong nội dung của chương này chúng tôi sẽ đề cập đến cách phân tích các tham số đó
bằng trình ứng dụng descriptive statistics. Trong SPSS có rất nhiều trình ứng dụng có

20

thể tính toán được các tham số thống kê mô tả hay nói cách khác trình ứng dụng
descriptive statistics có thể được thực hiện từ các trình ứng dụng khác, ví dụ từ trình
ứng dụng General Linear Model hay Compare means.
3.1. Phân tích thống kê mô tả trong trường hợp tập hợp số liệu không phân nhóm
Ví dụ 12. Hảy tính toán các tham số thống kê mô tả của năng suất lúa trong ví
dụ 2.
Chúng ta có thể thực hiện theo các bước sau :
 Bước 1: Nạp số liệu vào SPSS
 Bước 2: Vào trình ứng dụng descriptive statistics (hình 15)
 Bước 3 : Lựa chọn biến cần được thực hiện thống kê mô tả (hình 15)
 Bước 4: Lựa chọn các tham số thống kê cần tính toán (hình 15)


Hình 15. Phân tích thống kê mô tả khi số liệu không phân nhóm
Trình ứng dụng descriptive statistics này có thể tính toán được một số tham số
thống kê như trung bình (mean), sum (tổng), độ lệch chuẩn (Std. deviation), phương sai
(variance), sai số của số trung bình (S.E. mean), khoảng biến động (range), giá trị nhỏ
nhất (minimum) và giá trị lớn nhất (maximum). Một số tham số thống kê khác thông
thể tính tự động từ trình ứng dụng này ví dụ trung vị.

21

Bảng 7. Kết quả phân tích thống kê mô tả số liệu ví dụ 2
n Range

Min Max Sum Mean
Std.
Error
Std.
Deviation
Variance
20

35927

2606

38533

130069

6503,45

1701,501

7609,345

57902132


3.2. Phân tích thống kê mô tả trong trường hợp tập hợp số liệu phân nhóm
Có rất nhiều trình ứng dụng khác nhau có thể phân tích thống kê mô tả trong
trường hợp số liệu phân nhóm ví dụ chúng ta có thể sử dụng Compare means hay
General Linnear Model. Nói cách khác phân tích thống kê mô tả có thể được thực hiện

với các phân tích khác như phân tích hồi quy và phân tích phương sai.
Vídụ 13. Hãy tính toán các tham số thống kê mô tả của năng suất lúa theo các
công thức phân bón khác nhau trong ví dụ 2.
Ta có thể thực hiện theo các bước sau :
 Bước 1 : Nạp số liệu vào SPSS
 Bước 2: Vào trình ứng dụng phân tích thống kê mô tả từ compare means
( so sánh các trung bình), hình 15.

Hình 15. Phân tích thống kê mô tả từ compare means
 Bước 3: Lựa chọn biến cần tính toán thống kê mô tả và biến phân nhóm
(Hình 15).
 Bước 4 : Lựa chọn các chỉ số tham số thống kê cần tính toán

22

Trình ứng dụng này có thể tính toán được rất nhiều tham số thống kê mô tả. Có
thể nói rằng trình ứng dụng này có thể tính toán được hầu như toàn bộ các tham số
thống kê mô tả.
Kết quả phân tích thống kê mô tả ví dụ 13 được thể hiện ở bảng 8. Những kết
quả này hoàn toàn có thể được copy từ kết quả đầu ra của SPSS sang các phần mềm
khác như Microsoft Word, Excel hay Powerpoint. Cách thức copy hay cắt án hoàn toàn
tương tự như trong Microsoft Word, Excel hay Powerpoint. Trong một số trường hợp,
ví dụ khi ta muốn làm tròn số ta có thể copy vào Excel trước để làm tròn số, hay để
tính toán thêm một tham số thống kê, sau đó copy qua các phần mềm văn bản khác để
làm báo cáo.
Bảng 8. Kết quả phân tích mô tả năng suất lúa ở các mức phân bón khác nhau
CT
phân
bón Mean

N
Std.
Deviation

Median

Std.
Error
of
Mean Sum

Min

Max

Range

Variance

Geo.
Mean

N0 3,1

4,0

0,5

3,0

0,3

12,5

2,6

3,9

1,2

0,3

3,1

N1 4,7

4,0

0,2

4,7

0,1

18,9

4,6

4,9

0,4

0,0

4,7

N2 4,5

4,0

0,4

4,5

0,2

17,8

3,9

4,9

1,0

0,2

4,4

N3 5,7

4,0

0,3

5,8

0,2

22,9

5,3

6,0

0,8

0,1

5,7

N4 5,8

4,0

0,2

5,9

0,1

23,3

5,5

6,0

0,5

0,0

5,8

Total

4,8

20,0

1,1

4,8

0,2

95,4

2,6

6,0

3,4

1,1

4,6


Trong đó Mean = Trung bình, N=số quan sát, Std.Deviation = Độ lệch chuẩn,
Median = Trung vị, Std. Error of Mean = Sai số của số trung bình, Sum = Tổng, Min =
Giá trị bé nhất, Max = Giá trị lớn nhất, Range = Khoảng biến động, Variance = Phương
sai và Geometric Mean = Trung bình nhân.
Ngoài ra, cho ví dụ 13 ta có thể phân tích thống kê mô tả từ trình ứng dụng
General Linnear Model. Các bước như sau :
 Bước 1 : Nạp số liệu vào SPSS
 Bước 2: Vào trình ứng dụng General Linear Model (hình 16)
 Bước 3 : Khai báo biến phụ thuộc (dependent variables) và biến độc lập
(fixed factors)(hình 16)
 Bước 4 : Vào trình ứng dụng thống kê mô tả trong option (hình 16)
Trình ứng dụng thống kê mô tả trong option không cho phép chúng ta lựa chọn
các tham số thống kê mô tả cần tính toán mà luôn luôn cho kết quả mặc định. Kết quả
đó bao gồm : Mean = Trung bình, Std. deviation = Độ lệch chuẩn, và N = Số lần lặp lại
(Số đơn vị thí nghiệm nhận cùng một nghiệm thức). Một lưu ý là có rất ít các phần
mềm cho phép mặc định tính CV% (hệ số biến dị). Do vậy để có thể tính được CV%

23

chúng ta cần phải tính tiếp sau khi đã có kết quả độ lệch chuẩn và trung bình. Kết quả
phân tích thống kê mô tả của ví dụ 3 ứng dụng theo General Linear model được thể
hiện ở bảng 9.

Hình 16. Phân tích thống kê mô tả từ General Linear Model

BÀI 4. PHÂN TÍCH PHƯƠNG SAI
Phân tích phương sai là một trong những cách để kiểm tra giả thuyết, ngoài các
cách khác như kiểm tra t, kiểm tra khi bình phương. Phân tích phương sai dựa trên hàm
phân bố F. Bản chất của phân tích phương sai dựa trên sự sai khác giữa phương sai do
yếu tố thí nghiệm gây nên và phưong sai do yếu tố ngẫu nhiên gây nên. Điều kiện để
phân tích phương sai là số liệu trong mỗi công thức phân bố chuẩn và số liệu của các