BÀI GIẢNG ỨNG DỤNG TIN HỌC TRONG THIẾT KẾ THÍ NGHIỆM VÀ XỬ LÝ SỐ LIỆU (Phương pháp nghiên cứu nâng cao) part 9 ppsx

41
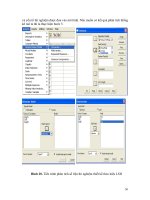
• Bước 4 (B4): Sắp xếp các cột “số ngẫu nhiên” và “chất sinh trưởng”
theo thứ tự tăng dần hoặc giảm dần của “số ngẫu nhiên”.



Hình 20. Cố định các giá trị ngẫu nhiên vừa tạo ra
Kết quả của quá trình ngẫu nhiên hóa ta có chậu 1 nhận CT2, chậu 2 nhận
CT1, chậu 3 nhận CT3, chậu 4 nhận CT3 chậu 24 nhận CT2.

6.2. Ngẫu nhiên hóa trong thiết kế thí nghiệm kiểu LSD
Ví dụ 18. Một nhóm nghiên cứu quan tâm đến ảnh hưởng của các giống
ngô đến năng suất ngô. Thí nghiệm được thiết kế theo kiểu LSD với 3 giống ngô
A, B, D và giống
đối chứng C. Hảy thiết kế thí nghiệm.
Quá trình thiết kế thí nghiệm hay áp dụng quy tắc ngẫu nhiên của thí
nghiệm thiết kế theo kiểu LSD được thực hiện theo các bước sau:
• Bước 1: Chọn ngẫu nhiên một hình vuông la tinh chuẩn. Trong ví dụ
này ta chọn hình vuông la tin chuẩn 4x4. Thông thường các sách thiết kế thí
nghiệm trong nông nghiệp có phụ lục các hình vuông la tinh chuẩn theo các kích
thước khác nhau. Lưu ý: Chúng ta có thể tạo ra hình vuông la tinh chuẩn

A B C D
B C D A
C D A B
D A B C

Hình 21. Hình vuông la tinh chuẩn 4x4

42

• Bước 2: Ngẫu nhiên hóa trật tự của hàng ngoại trừ hàng thứ nhất.
Quá trình ngẫu nhiên hóa hoàn toàn có thể sử dụng hàm RAND() như trình bày ở
trên. Kết quả được thể hiện ở hình 22.

A B C D
C D A B
D A B C
B C D A
Hình 22. Hình vuông la tinh chuẩn 4x4 sau khi đã được ngẫu nhiên hóa trật
tự của hàng
• Bước 3: Ngẫu nhiên hóa trật tự của cột. Quá trình ngẫu nhiên hóa
hoàn toàn có thể sử dụng hàm RAND() như trình bày ở trên. Kết quả được thể
hiện ở hình 23.

A D C B
C B A D
D C B A
B A D C

Hình 23. Hình vuông la tinh chuẩn 4x4 sau khi đã được ngẫu nhiên hóa trật
tự của hàng và trật tự của cột
Sau khi hoàn thành 3 bước ngẫu nhiên hóa thì đồng thời chúng ta cũng
hoàn thành thiết kế thí nghiệm.

BÀI 7. PHÂN TÍCH HỒI QUY
Phân tích phương sai giúp xác định ảnh hưởng hay không ảnh hưởng của
biến độc lập lên biến phụ thuộc, chứ không thể lượng hóa được ảnh hưởng của
biến độc lập lên biến phụ
thuộc. Để lượng hóa được ảnh hưởng của biến độc lập
lên biến phụ thuộc, chúng ta phải giải quyết bằng phân tích hồi quy. Phân tích hồi

quy là một lĩnh vực rất rộng có thể khái quát thành một số nội dung chính như:
Hồi quy đơn biến, hồi quy đa biến, hồi quy tuyến tính và hồi quy phi tuyến tính.
Trong phạm vi của chương trình này chúng tôi chỉ giới thiệu cách phân tích hồi
quy đơn biế
n.
Ví dụ 19. Một nhóm nghiên cứu quan tâm đến ảnh hưởng của hàm lượng
lân đến năng suất lúa. Nhóm nghiên cứu đã tiến hành nghiên cứu và thu thập được
số liệu ở bảng 21.
Có ba vấn đề chính trong phân tích hồi quy
• Kiểm tra mức độ tin cậy của hệ số hồi quy

43
• Kiểm tra mức độ tin cậy của các hệ số hồi quy
• Xác định mức độ giải thích của hệ số hồi quy

Bảng 21. Ảnh hưởng của hàm lượng lân đến năng suất lúa
Hàm lượng lân Năng suất (100 kg/ha)
0,058 63,700
0,057 62,300
0,035 56,200
0,054 58,600
0,046 48,100
0,048 45,300
0,051 53,800
0,045 45,300
0,050 52,400
0,056 60,900
0,056 60,000
0,055 60,000
0,049 46,700

0,050 51,600
0,052 53,800
0,045 43,900
0,057 55,000
0,056 62,300
0,058 56,000
0,058 66,600
0,047 45,300

Quá trình phân tích hồi quy có thể diễn ra theo các bước sau đây:
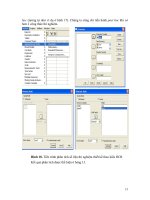
• Bước 1: Nạp số liệu từ EXCEL vào SPSS
• Bước 2: Lựa chọn hồi quy đơn biến (hình 24)
• Bước 3: Xác định mô hình và khai báo biến độc lập và biến phụ thuộc
(hình 24). Đây là hồi quy đơn biến tuyến tính cho nên có dạng như sau: y = bx + a.

44
Trong đó y là biến phụ thuộc (năng suất lúa), x là biên độc lập (hàm lượng lân), b
là hệ số gốc hay còn gọi là hệ số hồi quy, a là hằng số.


Hình 24. Các bước tiến hành phân tích hồi quy đơn biến.

Kết quả thu được như sau:

Bảng 22. Mức độ ý nghĩa của mô hình

Qua kết quả ở bảng 22 ta có thể kết luận rằng mô hình có thể giải thích
được sự biến động của năng suất lúa (P <0,01). Giả thuyết H
0
mà kết quả ở bảng

21 kiểm tra là: các tham số a và b =0, có nghĩa là mô hình không giải thích được
sự biến động của năng suất. Giả thuyết H
A
là ít nhất một tham số khác không có
nghĩa là hoặc a khác 0 hoặc b khác 0. Cách giải thích các thành phần trên bảng
ANOVA
b
431,101 1 431,101 15,553 ,001
a
526,651 19 27,718
957,751 20
Regression
Residual
Total
Model
1
Sum of
Squares
df Mean Square F Sig.
Predictors: (Constant), lan
a.
Dependent Variable: nangsuat
b.

45
phân tích phương sai ở bảng 22 hoàn toàn tương tự như phần phân tích ANOVA
đã nêu trong mục V.
• Model = Mô hình giải thích sự biến động của năng suất lúa gồm có
hai thành phần (i) thành phần do hồi quy giải thích (regression) và thành phần do
ngẫu nhiên giải thích (error).

• Sum of square = Tổng các bình phưong
• df = Độ tự do
• Mean Square = ước tính của phương sai
• F = Giá trị F tính toán
• Sig. = Mức ý nghĩa

Sau khi kiểm tra mức ý ngh
ĩa của mô hình ta phải kiểm tra mức độ tin cậy
của các hệ số hồi quy (bảng 22).
Bảng 23. Giá trị các tham số và mức ý nghĩa của các tham số trong phương
trình hồi quy
Coefficients(a)
Model
Unstandardized
Coefficients t Sig.
B Std. Error
1 (Constant) 14,102766 10,34728459 1,362944 0,188836

Hàm
lượng lân 786,37295 199,3992758 3,94371 0,000871
Dependent Variable: Năng suất

Qua bảng 23 ta có thể xác định được phương trình hồi quy như sau: Năng
suất lúa = 14,103 + 786,37 x hàm lượng lân. Giả thuyết H
0
của kiểm tra trong
bảng 23 là mỗi tham số =0 và giả thuyết H
A
là mỗi tham số khác 0. Khi giá trị của
tham số khác 0 thì thực sự nó có ảnh hưởng đến biến phụ thuộc. Các tham số trong

bảng 23 có thể được giải thích như sau:
• B = Các hệ số cần ước tính. Trong hồi quy đơn biến như ví dụ này
thì có 2 hệ số cần ước tính. Constant = Giá trị của hàng số = a =
14,103; Hàm lượng lân = b=786,37
• Std. Error = Sai số của số trung bình của ước tính
• t= Giá trị t tính toán. Giá trị này chính là B/Std.Error
•
Sig. = Mức ý nghĩa. Qua bảng trên ta thấy rằng hệ số b = 786,37 thực
sự khác 0 ( P <0,05).