Ma trận, Đề, Đáp án KH2 Toán 9

Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
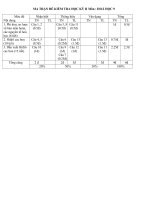
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
NĂM HỌC: 2009 - 2010 – MÔN: TOÁN 9
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 1 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2
ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010
Môn: TOÁN 9 - Thời gian làm bài: 90 phút
Bài 1. (1,5 điểm)
Phát biểu và chứng minh định lí tứ giác nội tiếp.
Bài 2. (1,0 điểm)
Giải các hệ phương trình
3x y 5
5x 2y 23
− =


+ =

Bài 3. (2,0 điểm)
Cho phương trình 7x
2
+ 2(m – 1)x – 1 = 0 (*) với m là tham số.
a) Giải phương trình (*) khi m = –2.
b) Chứng tỏ rằng phương trình (*) luôn có hai nghiệm trái dấu với mọi m.
Bài 4. (2,0 điểm)
Giải bài toán bằng cách lập phương trình.
Một xe khách và một xe du lịch khởi hành đồng thời từ A để đi đến B. Biết vận
tốc của xe du lịch lớn hơn vận tốc xe khách là 20km/h. Do đó nó đến B trước xe khách 50
phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100km.

Bài 5. (1,0 điểm) Cho phương trình x
2
– px – 228p = 0, với p là số nguyên tố.
Tìm p để phương trình có hai nghiệm nguyên.
Bài 6. (2,5 điểm)
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tia tiếp tuyến với
nửa đường tròn tại A và B. Trên tia Ax lấy điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng ∆MON ∽ ∆APB.
b) Chứng minh AM . BN = R
2
.
c) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 2 -
ĐỀ DỰ KIẾN
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2 HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010 - Môn: TOÁN 9
Bà
i
Nội dung Điểm
1
Trong một tứ giác nội tiếp, tổng hai góc đối diện bằng 180
0
. 0,5
GT Tứ giác ABCD nội tiếp (O).
KL
µ
µ
µ
µ

0
0
A C 180
B D 180
+ =
+ =
Ta có tứ giác ABCD nội tiếp đường tròn (O) nên :
µ
1
A
2
=
sđ
¼
BCD
(định lí góc nội tiếp)
µ
1
C
2
=
sđ
¼
DAB
(định lí góc nội tiếp)
Suy ra
µ
µ
¼
¼

1
A C (BCD DAB)
2
+ = +
Mà sđ
¼
BCD
+ sđ
¼
DAB
= 360
0
nên
µ
µ
0
A C 180+ =
Chứng minh tương tự
µ
µ
0
B D 180+ =
1,0
2
3x y 5
5x 2y 23
− =


+ =


⇔
6x 2y 10
5x 2y 23
− =


+ =

⇔
11x 33
5x 2y 23
=


+ =

⇔
x 3
15 2y 23
=


+ =

⇔
x 3
y 4
=



=

Vậy: Nghiệm của hệ phương trình (x; y) = (3; 4).
1,0
3
7x
2
+ 2(m – 1)x – 1 = 0 (*)
a) Khi m = –2 (*) ⇔ 7x
2
– 6x – 1 = 0 ⇔
x 1
1
x
7
=


−

=

1,0
b) Phương trình (*) có
a 7 0
ac 0
c 1 0
= >


⇒ <

= − <

Suy ra phương trình (*) có hai nghiệm phân biệt x
1
và x
2
.
Theo hệ thức Vi – ét:
1 2
c 1
x .x 0
a 7
−
= = <
⇒ x
1
, x
2
trái dấu.
Vậy phương trình (*) luôn có hai nghiệm x1, x2 trái dấu với mọi m.
1,0
4 Gọi vận tốc thực của xe khách là x (km/h). (Đk: x > 0). 0,25
Vận tốc của xe du lịch là: x + 20 (km/h) 0,25
Thời gian xe khách đi là:
100
x
(h) và Thời gian xe du lịch đi là:
100

20+x
(h)
0,25
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 3 -
O
A
B
C
D
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
Bà
i
Nội dung Điểm
Đổi 50 phút =
5
6
h
Theo đề bài ta có phương trình:
100 100 5
20 6
+ =
+x x
0,5
Giải phương trình được: x
1
= 40; x
2
= 60 (loại). 0,5
Vậy: Vân tốc của xe khách là 40 km/h.
Vân tốc của xe du lịch là 60 km/h.

0,25
5
Phương trinh x
2
– px – 228 = 0 có ∆ = p
2
+ 912p >0 do p là số nguyên tố.
0,25
Để phương trình có hai nghiệm nguyên thì ∆ là số chính phương.
Ta có: p
2
+ 912p = p(p + 912)
⇒ (p + 912) ⋮ p ⇒ 912 ⋮ p
Vì 912 = 2
4
.3.19 nên p ∈ {2; 3; 19}
0,25
* Với p = 2 thì ∆ = 1828 không phải là số chính phương.
* Với p = 3 thì ∆ = 2745 không phải là số chính phương.
* Với p = 19 thì ∆ = 17689 = 133
2
.
0,25
⇒
133.∆ =
Phương trình có hai nghiệm nguyên x
1
= 76; x
2
= −57.

Vậy với p = 19 thì phương trình x
2
– px – 228 = 0 có hai nghiệm nguyên.
0,25
4
a) Tứ giác AMPO có:
·
·
0 0 0
MAO MPO 90 90 180+ = + =

Suy ra tứ giác AMPO nội tiếp.
Suy ra
·
·
PMO PAO=
(1) hai góc nội tiếp cùng
chắn
»
OP
của đường tròn ngoại tiếp tứ giác
AMPO).
Tứ giác OPNB có:
·
·
OPN OBN+
= 90
0
+ 90
0

= 180
0
Suy ra tứ giác OPNB nội tiếp.
Suy ra
·
·
PNO PBO=
(2) hai góc nội tiếp cùng
chắn
»
OP
của đường tròn ngoại tiếp tứ giác
OPNB).
Từ (1) và (2) suy ra: ∆MON ∽ ∆APB (g – g)
Mặt khác ta có
·
0
APB 90=
(góc nội tiếp chắn nửa đường tròn (O)).
Vậy ∆MON và ∆APB là hai tam giác vuông đồng dạng.
0,25
0,25
0,25
0,25
0,25
0,25
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có: AM = MP và PN = NB
⇒AM . BN = MP . PN = OP
2
= R

2
(hệ thức lượng trong tam giác vuông).
0,25
0,25
c) Bán kính của hình cầu bằng R.
Vậy thể tích của hình cầu là:
4
V
3
3
= .π.Ρ
0,5
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 4 -
x
y
H
O
A
B
P
M
N
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
(Học sinh giải cách khác, đúng vẫn ghi điểm tối đa)
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 5 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
NĂM HỌC: 2009 - 2010 – MÔN: TOÁN 9
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 6 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên

TRƯỜNG THCS SỐ 2
ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010
Môn: TOÁN 9 - Thời gian làm bài: 90 phút.
(Đề có 02 trang)
Họ và tên học sinh: Lớp :
Số báo danh:
Giám thi 1 (Họ tên, ký) Giám thị 2 (Họ tên, ký) Số phách

Giám khảo 1 Giám khảo 2 Điểm thi Mã phách

A. Trắc nghiệm khách quan. (3,0 điểm) Thời gian: 20 phút (Không kể thời gian giao đề).
I. Khoanh tròn chỉ một chữ cái in hoa đứng trước câu trả lời đúng trong các câu sau:
Câu 1: Phương trình 4x – 3y = –1 nhận cặp số nào sau đây làm nghiệm ?
A. (–1; –1) B. (–1; 1) C. (1; –1) D. (1; 1)
Câu 2: Hệ phương trình
2x y 3
x y 1
− + = −


− =

có nghiệm (x; y) là:
A. (1; −1) B. (2; –1) C. (2; 1) D. (0; –1)
Câu 3: Biết đồ thị hàm số y = ax
2
đi qua điểm A(–2; 2). Thế thì a bằng:
A.
1

4
B. –
1
4
C.
1
2
D. –
1
2

Câu 4: Điểm nào sau đây thuộc đồ thị hàm số y = –
1
4
x
2
A. M(–2; 1) B. N(4; 4) C. P(2; 1) D. Q(–4; –4)
Câu 5: Phương trình nào sau đây là phương trình bậc hai một ẩn:
A.
2
5
2x 3 0
x
+ − =
B.
2
5x 2x 1 x+ = −
C. x
3
– 4x + 3 = 0 D. 3x

4
+ 2x
2
– 5 = 0
Câu 6: Nếu phương trình ax
2
+ bx + c = 0 (a
≠
0) có a + b + c = 0 thì:
A. x
1
= 1, x
2
=
c
a
B. x
1
= –1, x
2
=
c
a
C. x
1
= 1, x
2
= –
c
a

D. x
1
= –1, x
2
= –
c
a
Câu 7: Nếu hai số có tổng S = –5 và tích P = –14 thì hai số đó là nghiệm của phương trình:
A. x
2
+ 5x + 14 = 0 B. x
2
– 5x + 14 = 0 C. x
2
+ 5x – 14 = 0 D. x
2
– 5 x – 14 = 0
Câu 8: Phương trình nào sau đây có hai nghiệm phân biệt:
A. x
2
– 6x + 9 = 0 B. x
2
+ 4x + 5 = 0 C. x
2
+ 4 = 0 D. 2x
2
+ x – 1 = 0
Câu 9: Cho đường tròn (O) đường kính AB, M là điểm trên đường tròn sao cho
·
MAB

= 30
0
. Khi
đó số đo của cung MA là:
A. 30
0
B. 60
0
C. 90
0
D. 120
0
Câu 10: Cho tứ giác ABCD nội tiếp đường tròn, biết
µ
A
=115
0
,
µ
B
=75
0
. Hai góc C và D có số đo là:
A.
µ
µ
0 0
C 115 ;D 75= =
B.
µ

µ
0 0
C 75 ;D 115= =
C.
µ
µ
0 0
C 65 ;D 105= =
D.
µ
µ
0 0
C 105 ;D 65= =
II. Đúng ghi “Đ” sai ghi “S” vào ô trống:
Câu 11: Công thức để tính thể tích của hình trụ có bán kính đường tròn đáy bằng R, chiều cao
bằng h là:
2
4
V R h
3
= π
. mm
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 7 -
ĐỀ DỰ KIẾN
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
Câu 12: Công thức tính thể tích của hình nón có bán kính đường tròn đáy bằng R, chiều cao bằng
h là:
2
1
V R h

3
= π
mm
TRƯỜNG THCS SỐ 2 ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010
Môn: TOÁN 9 - Thời gian làm bài: 90 phút.
(Đề có 02 trang)
B. Tự luận. (7,0 điểm) Thời gian: 70 phút (Không kể thời gian giao đề).
Bài 1. (1,0 điểm)
a) Giải các hệ phương trình
3x y 5
5x 2y 23
− =


+ =

b) Giải phương trình x
2
+ 2009x – 2010 = 0.
Bài 2. (2,0 điểm)
Một ca nô xuôi dòng từ A đến B dài 120km rồi quay trở về lại A mất 11giờ. Tính vận tốc
thực của ca nô, biết vận tốc của dòng nước là 2km/h.
Bài 3. (1,0 điểm)
Cho phương trình x
2
– px – 228p = 0, với p là số nguyên tố.
Tìm p để phương trình có hai nghiệm nguyên.
Bài 3. (3,0 điểm)
Cho tam giác ABC nội tiếp trong đường tròn (O; R). Các đường cao BE và CF cắt nhau tại

H, AH cắt BC tại D và cắt đường tròn (O) tại M.
a) Chứng minh tứ giác AEHF, tứ giác BCEF nội tiếp.
b) Chứng minh rằng BC là tia phân giác của góc EBM.
c) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF; K là tâm đường tròn ngoại tiếp tứ giác
BCEF. Chứng minh IE là tiếp tuyến của đường tròn (K).
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 8 -
ĐỀ DỰ KIẾN
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2 HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010 - Môn: TOÁN 9
A. Trắc nghiệm khách quan. (3,0 điểm).
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Đáp án A A C D B A C D D C S Đ
Điểm 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25
B. Tự luận (7,0 điểm).
Bài Nội dung Điểm
1
a)
3x y 5
5x 2y 23
− =


+ =

⇔
6x 2y 10
5x 2y 23
− =



+ =

⇔
11x 33
5x 2y 23
=


+ =

⇔
x 3
15 2y 23
=


+ =

⇔
x 3
y 4
=


=

Vậy: Nghiệm của hệ phương trình (x; y) = (3; 4).
0,5
b)

2
x 1
x 2009x 2010 0
x 2010
=

+ − = ⇔

= −

0,5
2
Gọi vận tốc thực của ca nô là x km/h. (Đk: x > 0). 0,25
Vận tốc xuôi dòng là: x + 2
Vận tốc ngược dòng là: x – 2
Thời gian khi xuôi dòng là:
120
2x +
(giờ)
0,25
Thời gian khi ngược dòng là:
120
2x −
(giờ) 0,25
Theo đề bài ta có PT:
120 120
11
2 2x x
+ =
+ −

0,5

( ) ( ) ( ) ( )
( ) ( )
2
2
120 2 120 2 11 2 2 11 240 44 0
' 120 11. 44 14884 0 ' 122
⇔ − + − = − + ⇔ − − =
∆ = − − − = > ⇒ ∆ =
x x x x x x

1 2
120 122 120 122 2
22;
11 11 11
x x
+ −
= = = = −

0,5
Vậy: Vân tốc thực của ca nô là 22 km/h. 0,25
3
Phương trinh x
2
– px – 228 = 0 có ∆ = p
2
+ 912p >0 do p là số nguyên tố.
0,25
Để phương trình có hai nghiệm nguyên thì ∆ là số chính phương.

Ta có: p
2
+ 912p = p(p + 912)
⇒ (p + 912) ⋮ p ⇒ 912 ⋮ p
Vì 912 = 2
4
.3.19 nên p ∈ {2; 3; 19}
0,25
* Với p = 2 thì ∆ = 1828 không phải là số chính phương.
* Với p = 3 thì ∆ = 2745 không phải là số chính phương.
* Với p = 19 thì ∆ = 17689 = 133
2
.
0,5
⇒
133.∆ =
Phương trình có hai nghiệm nguyên x
1
= 76; x
2
= −57.
0,25
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 9 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
Bài Nội dung Điểm
Vậy với p = 19 thì phương trình x
2
– px – 228 = 0 có hai nghiệm nguyên.
4
a) Xét tứ giác AEHF có :

·
·
·
·
0
0
0
AEH 90 (gt)
AEH AFH 180
AFH 90 (gt)

=

⇒ + =

=



⇒ tứ giác AEHF nội tiếp (có tổng hai góc đối bằng 180
0
)
Xét tứ giác BFEC có:
·
0
BFC 90=
( gt);
·
0
CEB= 90

( gt)
Suy ra E, F cùng nhìn đoạn BC dưới cùng một góc bằng 90
0
⇒ E, F ∈ ( K;
BC
2
) (Theo quỹ tích cung chứa góc)
0,25
0,25
0,25
0,25
b) Ta có:

·
·
¼
1
MAC = CBM = sdMC
2
(hai góc nội tiếp cùng chắn cung MC của (O)) (1)
Tứ giác BCEF nội tiếp (K) ⇒
·
·
»
1
EBC= EFC = sdEC
2
(hai góc nội tiếp cùng chắn
cung EC của (K)) (2)
Lại có tứ giác AEHF nội tiếp trong (I) ⇒

·
·
»
1
EFH= EAH = sdEH
2
(hai góc nội tiếp
cùng chắn cung EH của (I)) (3)
Từ (1); (2); (3) suy ra
·
·
CBM = EBC
⇒ BC là tia phân giác của góc EBM.
0,25
0,25
0,25
0,25
c) Gọi I, K lần lượt là trung điểm của AH và BC ⇒ I, K là tâm đường tròn ngoại
tiếp các tứ giác AEHF và BCEF (theo cmt)
Nối IE, KE ta có:
* ∆AIE cân tại I (IA = IE) ⇒
·
·
IAE = IEA
(4)
* ∆KEC cân tại K (KE = KC) ⇒
·
·
KEC = KCE
(5)

* ∆ADC vuông tại D (gt) ⇒
·
·
0
DAC + DCA = 90
(6)
Từ (4); (5); (6) suy ra
0
ˆ ˆ
IEH + KEH = 90
⇒ IE ⊥ KH ⇒ IE là tiếp tuyến của (K) tại E.
0,25
0,25
0,25
0,25
(Học sinh giải cách khác, đúng vẫn ghi điểm tối đa)
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 10 -
H
K
K
M
E
F
D
O
C
A
B
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II

NĂM HỌC: 2009 - 2010 – MÔN: TOÁN 9
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 11 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2 ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010
Môn: TOÁN 9 - Thời gian làm bài: 90 phút.
(Đề có 03 trang)
Họ và tên học sinh: Lớp :
Số báo danh:
Giám thi 1 (Họ tên, ký) Giám thị 2 (Họ tên, ký) Số phách

Giám khảo 1 Giám khảo 2 Điểm thi Mã phách

A. Trắc nghiệm khách quan. (4,0 điểm) Thời gian: 20 phút (Không kể thời gian giao đề).
I. Khoanh tròn chỉ một chữ cái in hoa đứng trước câu trả lời đúng trong các câu sau:
Câu 1. Hệ phương trình
2 3
1
x y
x y
− + = −


− =

có nghiệm (x ; y) là :
A. (1; −1) B. (2; −1) C. (2; 1) D. (0; −1)
Câu 2. Điểm N(2 ; 5) thuộc đồ thị hàm số y = mx
2
+3 khi:

A. m =
2
1
B. m =
2
1
−
C. m = 2 D. m =−2
Câu 3. Phương trình (k
2
– 4)x
2
+ 2(k + 2)x + 1 = 0 có một nghiệm duy nhất nghiệm khi k
bằng:
A. −2 B. 2 C. ±2 D. 4
Câu 4. Cặp số nào sau đây là nghiệm của phương trình
2 1
1
2
+ =



= −


x y
y
A.
1

0;
2
 
−
 ÷
 
B.
1
2;
2
 
−
 ÷
 
C.
1
0;
2
 
 ÷
 
D.
( )
1;0
Câu 5. Hệ phương trình
2 3
2 4
x y
x y
− =



+ =

có nghiệm là:
A.
10 11
;
3 3
 
 ÷
 
B.
2 5
;
3 3
 
−
 ÷
 
C.
( )
2;1
D.
( )
1; 1−

Câu 6. Cho hàm số
2
1

2
y x= −
. Kết luận nào sau đây là đúng?
A. Hàm số luôn luôn đồng biến.
B. Hàm số luôn luôn nghịch biến
C. Hàm số đồng biến khi x > 0, nghịch biến khi x < 0.
D. Hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Câu 7. Một cung tròn 60
0
của một đường tròn có bán kính R có độ dài là bao nhiêu?
A.
πR
l =
3
B.
3
l =
R
C.
π
3R
l =
D.
π
3
l =
R
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 12 -
ĐỀ DỰ KIẾN
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên

Câu 8. Độ dài cung 90
0
của đường tròn có bán kính
2
cm là:
A.
)(
2
2
cm
π
B. 2
)(2 cm
π
C.
)(
2
2
cm
π
D.
)(
2
1
cm
π
Câu 9. Khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt
là 15 cm, số đo cung là 120
0
thì diện tích xung quanh của hình nón là:

A . 75π cm
2
B. 80π cm
2
C. 45π cm
2
D. 15 cm
2
II. Hãy nối mỗi ý ở cột A với một ý ở cột B để có kết quả đúng:
A B
Ghép
1. Công thức để tính thể tích của hình trụ có bán
kính đường tròn đáy bằng R, chiều cao bằng h là:
2. Công thức tính thể tích của hình nón có bán kính
đường tròn đáy bằng R, chiều cao bằng h là:
3. Công thức tính thể tích hình cầu có bán kính R là:
a.
2
4
V R h
3
= π
b.
2
1
V R h
3
= π
c.
2

V R h= π
d.
3
4
V R
3
= π
1 +
2 +
3 +
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 13 -
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2 ĐỀ KIỂM TRA HỌC KỲ II
BÌNH NGUYÊN NĂM HỌC 2009 – 2010
Môn: TOÁN 9 - Thời gian làm bài: 90 phút.
(Đề có 03 trang)
B. Tự luận. (6,0 điểm) Thời gian: 70 phút (Không kể thời gian giao đề).
Bài 1. ( 2điểm)
Cho phương trình
( )
2
x 2k 1 x 2k 2 0− − + − =
(ẩn x)
a. Chứng minh rằng phương trình luôn luôn có nghiệm với mọi k.
b. Tính tổng hai nghiệm của phương trình.
Bài 2 ( 2điểm)
Một ca nô xuôi dòng từ A đến B dài 120km rồi quay trở về lại A mất 11giờ. Tính vận
tốc thực của ca nô, biết vận tốc của dòng nước là 2km/h.
Bài 3. ( 3điểm)
Cho tam giác ABC nội tiếp trong đường tròn (O; R). Các đường cao BE và CF cắt

nhau tại H, AH cắt BC tại D và cắt đường tròn (O) tại M.
a. Chứng minh tứ giác AEHF, tứ giác BCEF nội tiếp.
b. Chứng minh rằng BC là tia phân giác của góc EBM.
c. Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF; K là tâm đường tròn ngoại tiếp
tứ giác BCEF. Chứng minh IE là tiếp tuyến của đường tròn (K).
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 14 -
ĐỀ DỰ KIẾN
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
TRƯỜNG THCS SỐ 2 HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KỲ I
BÌNH NGUYÊN NĂM HỌC 2009 – 2010 - Môn: TOÁN 9
A. Trắc nghiệm khách quan. (3,0 điểm).
Câu 1 2 3 4 5 6 7 8 9 II. Ghép
Đáp
án
A D B A C B B B C 1+c 2+b 3+d
Điểm 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25
0,2
5
0,25 0,25 0,25
B. Tự luận (7,0 điểm).
Bài Nội dung Điểm
1
a. Ta có:

( ) ( ) ( )
2 2
2 2
2 1 4 2 2 4 4 1 8 8 4 12 9 2 3∆ = − − − = − + − + = − + = −k k k k k k k k

0⇒ ∆ ≥ ∀k

Vậy phương trình luôn có nghiệm.
1,0
0,5
b. x
1
+ x
2
= 2k – 1 0,5
2
Gọi vận tốc thực của ca nô là x km/h. (Đk: x > 0). 0,25
Vận tốc xuôi dòng là: x + 2
Vận tốc ngược dòng là: x – 2
Thời gian khi xuôi dòng là:
120
2x +
(giờ)
0,25
Thời gian khi ngược dòng là:
120
2x −
(giờ) 0,25
Theo đề bài ta có PT:
120 120
11
2 2x x
+ =
+ −
0,5

( ) ( ) ( ) ( )

( ) ( )
2
2
120 2 120 2 11 2 2
11 240 44 0
' 120 11. 44 14884 0
' 122
x x x x
x x
⇒ − + − = − +
⇔ − − =
∆ = − − − = >
∆ =

1 2
120 122 120 122 2
22;
11 11 11
x x
+ −
= = = = −

0,5
Vậy: Vân tốc thực của ca nô là 22 km/h. 0,25
3a
Xét tứ giác AEHF có :
·
·
·
·

0
0
0
AEH 90 (gt)
AEH AFH 180
AFH 90 (gt)

=

⇒ + =

=



Suy ra tứ giác AEHF nội tiếp
(có tổng hai góc đối bằng 180
0
)
Xét tứ giác BFEC có:
·
0
BFC 90=
( gt);
·
0
CEB= 90
( gt)
Suy ra E, F cùng nhìn đoạn BC dưới cùng một góc bằng 90
0

⇒ E, F ∈ ( K;
BC
2
) (Theo quỹ tích cung chứa góc)
0,25
0,25
0,25
0,25
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 15 -
K
D
H
F
E
I
M
C
B
A
Võ Hoàng Chương – Gv: Trường THCS Số 2 Bình Nguyên
3b
Ta có:

·
·
¼
1
MAC = CBM = sdMC
2
(hai góc nội tiếp cùng chắn cung MC của (O)) (1)

Tứ giác BCEF nội tiếp (K) ⇒
·
·
»
1
EBC= EFC = sdEC
2
(hai góc nội tiếp cùng chắn
cung EC của (K)) (2)
Lại có tứ giác AEHF nội tiếp trong (I) ⇒
·
·
»
1
EFH= EAH = sdEH
2
(hai góc nội
tiếp cùng chắn cung EH của (I)) (3)
Từ (1); (2); (3) suy ra
·
·
CBM = EBC
⇒ BC là tia phân giác của góc EBM.
0,25
0,25
0,25
0,25
3c
Gọi I, K lần lượt là trung điểm của AH và BC ⇒ I, K là tâm đường tròn ngoại
tiếp các tứ giác AEHF và BCEF (theo cmt)

Nối IE, KE ta có:
* ∆AIE cân tại I (IA = IE) ⇒
·
·
IAE = IEA
(4)
* ∆KEC cân tại K (KE = KC) ⇒
·
·
KEC = KCE
(5)
* ∆ADC vuông tại D (gt) ⇒
·
·
0
DAC + DCA = 90
(6)
Từ (4); (5); (6) suy ra
0
ˆ ˆ
IEH + KEH = 90

⇒ IE ⊥ KH ⇒ IE là tiếp tuyến của (K) tại E.
0,25
0,25
0,25
0,25
(Học sinh giải cách khác, đúng vẫn ghi điểm tối đa)
Đề kiểm tra Học kỳ II – Năm học 2009 – 2010 Môn Toán 9 - 16 -