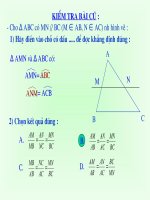T42.Bai 4: KHAI NIEM TAM GIAC DONG DANG

-
Nờu h qa ca nh lớ Ta-lột.
Lm bi tp sau:
Cho hỡnh veừ beõn, bieỏt
MN // BC.Tớnh ủoọ daứi x.
2
M
B
N
C
6,5
3
X
A

Nhóm 1
Nhóm 2
Nhóm 3

Nhìn vào hình vẽ hãy:
a) Viết các cặp góc bằng nhau?
b) Tính các tỉ số rồi so sánh
các tỉ số đó ?
3
2,5
2
B'
A'

C'
6
5
4
B
A
C
' ' ' ' ' '
; ;
A B B C C A
AB BC CA
1.Tam giác đồng dạng:

1.Tam giác đồng dạng:
a. Định nghĩa:
µ
µ
¶
µ
¶
µ
' ; ' ; '
' ' ' ' ' '
A A B B C C
A B A C B C
AB AC BC
= = =
= =
* Tam giác A’B’C’ gọi là đồng dạng
với tam

giác ABC nếu:
* Tam giác A’B’C’ đồng dạng với
tam giác ABC được kí hiệu là:
' ' '
A B C ABC∆ ∆
A'B' B'C' C'A'
= = = k
AB BC CA
k gọi là tỉ số đồng dạng

C¸c kh¼ng ®Þnh sau ®©y ®óng hay sai?
1. Hai tam giác bằng nhau
thì đồng dạng với nhau.
( Sai )
2. Hai tam giác đồng dạng
với nhau thì bằng nhau.
( §óng )
a
b
c
a
′
b
′
c
′
3
2,5
2
B'

A'
C'
6
5
4
B
A
C

1.Tam giác đồng dạng:
a. Định nghĩa:
µ
µ
¶
µ
¶
µ
' ; ' ; '
' ' ' ' ' '
A A B B C C
A B A C B C
AB AC BC
= = =
= =
* Tam giác A’B’C’ gọi là đồng dạng
với tam
giác ABC
nếu:
* Tam giác A’B’C’ đồng dạng với
tam giác ABC được kí hiệu là:

' ' '
A B C ABC∆ ∆
A'B' B'C' C'A'
= = = k
AB B C CA
k gọi là tỉ số đồng dạng
b. Tính chất:
+ Nếu
' ' '
A B C ABC∆ ∆
theo tỉ số đồng dạng k thì
' ' '
ABC A B C∆ ∆
theo tỉ số
1
k
+ Nếu và
' ' ' '' '' ''
A B C A B C∆ ∆
'' '' ''
A B C ABC∆ ∆
thì
' ' '
A B C ABC∆ ∆
+ Nếu thì
' ' '
A B C ABC∆ = ∆
' ' '
A B C ABC∆ ∆
đồng dạng k = 1.

theo tỉ số
đồng dạng

1.Tam giác đồng dạng:
a. Định nghĩa:
b. Tính chất:
' ' ' '' '' ''
A B C A B C∆ ∆
1
k
'' '' ''
A B C ABC∆ ∆
2
k
Bài tập 24 (SGK):
theo tỉ số đồng dạng
theo tỉ số đồng dạng
Hỏi:
' ' '
A B C ABC∆ ∆
theo tỉ số đồng dạng nào?
Cho

1.Tam giác đồng dạng:
a. Định nghĩa:
* Vì MN // BC nên
b. Tính chất:
?3 Nhìn vào hình
vẽ biết a // BC , hãy
điền các nội dung

thích hợp vào chỗ
chấm của các câu
sau:
a
N
C
M
B
A
·
AMN =
……
( cặp góc ……….
·
ABC
đồng vị )
·
ANM =
( cặp góc
·
ACB
………
* Vì MN // BC nên
đồng vị )
* Vì MN // BC nên theo hệ
quả của định lí Talet :
Vậy


AM MN

AC
= =
AMN ABC∆ ∆
AN
AB
BC
2. Định lí:
Nếu một đường thẳng
cắt hai cạnh của tam
giác và song song với
cạnh còn lại thì nó
tạo thành một tam giác mới đồng dạng
với tam giác đã cho.
Chứng minh:
N
Nếu một đường thẳng

Chú ý:
A
C
M
N
a
Định lí cũng đúng cho trường hợp đường thẳng a cắt
phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại
ΔAMN ABC∆
Ta cũng có:
C
B
B

A
NM
a
.
.


A
B
C
Cho
Cho
∆
∆
ABC.Từ điểm M trên cạnh AB
ABC.Từ điểm M trên cạnh AB
,
,
kẻ các tia song
kẻ các tia song


song với AC và BC
song với AC và BC
, chúng cắt BC và AC lần lượt tại
, chúng cắt BC và AC lần lượt tại
L và N.
L và N.

N
L
M
Bài tập :
Tìm các cặp tam giác đồng dạng

1.Tam giác đồng dạng:
a. Định nghĩa:
2. Định lí:
b. Tính chất:
a
N
C
M
B
A
µ
µ
¶
µ
¶
µ
' ; ' ; '
' ' ' ' ' '
A A B B C C
A B A C B C
AB AC BC
= = =

= =
nếu
+ Nếu
' ' '
A B C ABC∆ ∆
theo tỉ số k
' ' '
ABC A B C∆ ∆
thì theo tỉ số

1
k
' ' ' '' '' ''
A B C A B C∆ ∆
+ Nếu thì
' ' '
A B C ABC∆ = ∆
' ' '
A B C ABC∆ ∆
k = 1.
theo tỉ số
+ Nếu và
'' '' ''
A B C ABC∆ ∆
thì
' ' '
A B C ABC∆ ∆
Hướng dẫn về
nhà :
* Nắm vững định nghĩa, tính

chất, định lí về tam giác
đồng dạng.
* Bài tập về nhà: 25; 27; 28.
' ' '
A B C ABC∆ ∆
Nếu một đường thẳng cắt
hai cạnh của tam giác và song song với
cạnh còn lại thì nó
tạo thành một
tam giác mới
đồng dạng với
tam giác đã cho.
thì
∆ ∆ABC Amn
// ;ABC MN BC M AB∆ ∈
N AC∈
có
* Biết dựng tam giác đồng
dạng với tam giác cho trước
theo tỉ số đồng dạng.

Thales - Hy Lạp
(vào khoảng 624-547 TCN)

Thales - Hy Lạp
(vào khoảng 624-547 TCN)