các TH đồng dạng của tam giác vuông

B
A
C
A’ C’
B’
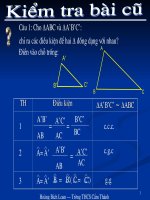
Th1: (g.g)
Cho hình vẽ sau. Áp dụng các trường hợp đồng dạng của
tam giác, hãy thêm điều kiện để ABC A’B’C’?
S
KiÓm tra

B
A C A’ C’
B’
Th1: (g.g)
Th2: (c.g.c)
Cho hình vẽ. Áp dụng các trường hợp đồng dạng của
tam giác, hãy thêm điều kiện để ABC A’B’C’?
S

TiÕt 48
TiÕt 48

B
A C A’

C’
B’
1/ ¸p dông c¸c trêng hîp ®ång d¹ng cña tam gi¸c
vµo tam gi¸c vu«ng
TH2 (c.g.c): NÕu thªm th× ∆ abc ∆a b c’ ’ ’
' ' ' '
AB AC
A B A C
=
S
∆
ABC vµ ∆A B C ’ ’ ’ cã A = A = 90’
0
TH1 (g.g): NÕu thªm B = B’ hoÆc C = C’ th× ∆ abc ∆a b c’ ’ ’
S

Bài 1: Hãy khoanh tròn vào chữ cái dưới
Bài 1: Hãy khoanh tròn vào chữ cái dưới
mỗi cặp tam giác đồng dạng:
mỗi cặp tam giác đồng dạng:
A
A’
B’
O
Q
P
I
R
Y
X

Z
X’
Y’
Z’
P
N
M
E
D
F
K
B
a)
b)
c) d)
6 3
6
5
10
5
3
5
2.5
2
4
10
∆
KIR ∆PQR (c.g.c)
S
∆

xyz ∆x y z (’ ’ ’ c.c.c)
S
8
4
∆
ABO ∆A B o (’ ’ g.g)
S
8,7
5,6

NHận xét:
- Nếu cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với
cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai
tam giác đồng dạng.
GT
KL
ABC, A B C , A=A=90
0
(1)
BC
C'B'
AB
B'A'
=
ABC A B C
S
- Từ (1) =>
2
AB-
2

BC
2
B'-A'
2
C'B'

2
BC
2
C'B'
2
AB
2
B'A'
==
Mà: (ĐL Py-Ta-go)
2
AC
2
AB
2
BC
2
C'A'
2
B'A'
2
C'B'
=+
=+

AC
C'A'

BC
C'B'
AB
B'A'
2
AC
2
C'A'

2
BC
2
C'B'
2
AB
2
B'A'
===>==
Vậy ABC A B C (c.c.c)
2/ Dấu hiệu đặc biệt nhận biết hai tam giác vuông dồng dạng
Định lí 1:
Do đó:
S
Chứng minh
B
A
C

A
C
B
Vậy theo em có mấy TH đồng dạng của tam giác vuông?

Bài 2: Cho hình vẽ, điền vào GT và
Bài 2: Cho hình vẽ, điền vào GT và
chứng minh: DEC = BCA
chứng minh: DEC = BCA
D
C
A
B
E
3
6
GT
KL DEC = BCA

Bài 2: Cho hình vẽ, điền vào GT và
Bài 2: Cho hình vẽ, điền vào GT và
chứng minh: DEC = BCA
chứng minh: DEC = BCA
D
C
A
B
E
3
6

GT DCE; ABC; D = A = 90
o

CE = EB; DC=3, AB=6
KL DEC = BCA

v
D = A = 90
0


∆
DCE ∆ACB
S
(Hai gãc t/@)
CE = EB



Bài 2
Bài 2
(PHT)
(PHT)
: Cho hình vẽ, điền vào GT và
: Cho hình vẽ, điền vào GT và
chứng minh: DEC = BCA
chứng minh: DEC = BCA
D
C
A

B
E
3
6
GT DCE; ABC; D = A = 90
o

CE = EB; DC=3, AB=6
KL DEC = BCA
CM:
• Có CE = EB (GT)
•Xét DCE và ABC có

D = A = 90
o
(GT)
Vậy DCE ABC (cạnh huyền
- cạnh góc vuông)

DEC = BCA (ĐN 2 đồng dạng)
CE
CB
=
DC
AB
Vì
=
3
6
1

2
=
1
2
CE
CB

Bµi t©p 3
Cho ∆A B C ®ång d¹ng víi ’ ’ ’ ∆ ABC víi tØ sè ®ång d¹ng
KÎ ®@êng cao AH vµ A H . Chønh minh:’ ’
2
k
ABC
S
C'B'A'
S
b/
k
AH
H'A'
a/
=
=
AB
B'A'
k =
∆ A B C ’ ’ ’ ∆ABC
S
GT
KL

AB
B'A'
k =
2
k
ABC
S
C'B'A'
S
b/
k
AH
H'A'
a/
=
=
A
B C
H
A’
H’
C’
B’

Bµi t©p 3
∆ A B C ’ ’ ’ ∆ABC
S
GT
KL
BC

C'B'
AC
C'A'
AB
B'A'
k ===
2
k
ABC
S
C'B'A'
S
b/
k
AH
H'A'
a/
=
=
A
B C
H
A’
H’
C’
B’
Chøng minh
a/ ∆A B C ’ ’ ’ ∆ABC => ∠B=∠B => ’ ∆ vu«ng A H B ’ ’ ’ ∆ vu«ngAHB (gãc nhän)
=>
S

S
k
AH
H'A'
AB
B'A'
==
2
kk.k
BC
C'B'
.
AH
H'A'
AH.BC
2
1
C'H'.B'A'
2
1
ABC
S
C'B'A'
S
b/ ====

Qua bài tập này em rút ra nhận xét gì?
Nhận xét:
Tỉ số hai đờng cao tơng ứng của hai tam giác đồng dạng bằng tỉ số
đồng dạng.

Tỉ số diện tích của hai tam giác đồng dạng bằng bình phơng tỉ số đồng
dạng.
Định lí 2
Định lí 3
3/ Tỉ số hai đờng cao, tỉ số diện tích của hai tam giác đồng dạng

Bài tập 4:
Hai tam giác vuông cân, có độ dài cạnh huyền của
tam giác thứ nhất gấp 3 lần cạnh huyền của tam giác
thứ hai. Gọi S
1
; S
2
lần l@ợt là diện tích của tam giác
thứ nhất và tam giác thứ hai, câu nào sau đây đúng.
a/ S
1
= 3S
2
b/ S
2
= 3S
1

c/ S
1
= 9S
2
d/ S
2

= 9S
1

x
GiảI
-
Vì hai tam giác vuông cân thì đồng dạng với nhau, tỉ số đồng dạng
là 3.
21
2
2
1
9ss 93
s
s
===

Bài tập 4
- Cho hình vẽ sau:
A
B
H
C
1/ Hãy chỉ ra các cặp tam giác đồng dạng trong hình vẽ .
a/ AHB CAB (góc nhọn B chung)
S
b/ CAB CHA (góc nhọn C chung)
S
c/ AHB CHA (g.g)
S

Bài tập 5
Cho tam giác ABC vuông ở A. Trên cạnh BC lấy điểm D. Hạ DE vuông góc
với AC, E thuộc AC biết DE=3cm; EC=5cm; và AC=20 cm . Tính AB?
A
B
D
C
E
GT
KL
( )
20cmAC 5cm;EC cmDE
ACE ACDE
BCD ; 90A ABC
0
===

=
;3
?=AB
BàI GIảI
Xét tam giác ABC và tam giác DEC có:
chung C
EA

==
0
90
}

=> ABC DEC ( g.g)
S
)(
.
cmAB
EC
AC
DE
AB
12
5
203
5
20
====
3
AB
hay
//////////////////////////////////////////////////////////////

Các trường hợp đồng dạng của tam giác vuông
A
B C B’ C’
A’
Th1: (g.g)

Các trường hợp đồng dạng của tam giác vuông
A
B C B’ C’
A’

Th1: (g.g)

Các trường hợp đồng dạng của tam giác vuông
A
B C B’ C’
A’
Th1: (g.g)

Các trường hợp đồng dạng của tam giác vuông
A
B C B’ C’
A’
Th1: (g.g)
Th2: (c.g.c)