BÀI GIẢNG ỨNG DỤNG TIN HỌC TRONG THIẾT KẾ THÍ NGHIỆM VÀ XỬ LÝ SỐ LIỆU (Phương pháp nghiên cứu nâng cao) part 6 ppt

26
lúa. Đó là biến động do yếu tố thí nghiệm gây nên (công thức phân bón) và biến
động do yếu tố ngẫu nhiên (tất cả những yếu tố còn lại = error)
• Sum of square = SS= Tổng các bình phương. Một cách cụ thể hơn
là tổng các bình phương độ lệch giữa các giá trị quan sát và trung bình tổng thể.

Bảng 10. Kết quả phân tích phương sai một nhân tố ở ví dụ 14
Kiểm tra ảnh hưởng giữa các nhóm (Tests of Between-Subjects Effects)
Biến phụ thuộc (Dependent Variable): Năng suất
Source S S df M S F Sig.
Corrected Model 19,25 4,00 4,81 38,25 0,00
Intercept 454,95 1,00 454,95 3615,56 0,00
Công thức phân bón 19,25 4,00 4,81 38,25 0,00
Error 1,89 15,00 0,13
Total 476,09 20,00
Corrected Total 21,14 19,00
R Squared=R
2
= ,911 (Adjusted R Squared =R
2
điểu chỉnh= ,887)

• df = độ tự do
• MS = Trung bình bình phương, chính là ước tính của phương sai.
Trung bình bình phương chính là tỷ số giữa tổng bình phương và độ tự do. Ví dụ
trung bình bình phương của công thức phân bón là 4,81, chính là tỷ số 19,25/4.
• F = Giá trị F tính toán. Mỗi giá trị F chính là tỷ số giữa mỗi trung
bình bình phương và trung bình bình phương ngẫu nhiên. Ví dụ giá trị F tính toán
của công thức phân bón là 38,25, chính là tỷ số 4,81/0,13.
• Sig. = Mức độ tin cậy (Significance)

• SS
Total
= SS
Intercept
+SS
Yếu tố thí nghiệm
+SS
error
= SS
Intercept
+SS
Công thức phân
bón
+SS
error

• SS
Corrected total
=SS
Yếu tố thí nghiệm
+ SS
error
= SS
Công thức phân bón
+ SS
error

Qua bảng 10 ta thấy rằng công thức phân bón đã ảnh hưởng đến năng suất
lúa, có nghĩa là bác bỏ giả thuyết H
0

đồng thời chấp nhận giả thuyết H
A
. Các công
thức phân bón khác nhau mang lại năng suất lúa khác nhau. Do chấp nhận giả
thuyết H
A
cho nên ta tiến hành phân tích post hoc để chỉ ra năng suất lúa ở công
thức phân bón nào thực sự khác với công thức nào.
Kết quả phân tích post hoc được thể hiện ở bảng 14.
• Mean difference= Sự sai khác giữ 2 trung bình cần so sánh.

27
• Std. Error = SD= Sai số chuẩn của sự sai khác giữa 2 giá trị trung
bình = Standard error of difference = sqrt (2xMSE/n).
 SQRT() là hàm để tính căn bậc 2
 MSE là ước tính của phương sai của sai số, trong bảng 10
MSE là 0,13
 n = số lần lặp lại, trong ví dụ này n =4
Bảng 11. Kết quả phân tích post hoc ví dụ 14
Đa so sánh (Multiple Comparisons)
Biến phụ thuộc (Dependent Variable): Năng suất
LSD = (M
1
-M
2
)/sqrt[MSE(1/n
1
+1/n
2
]

(I) CT
phân
bón
(J) CT
phân
bón
Mean
Difference
(I-J)
Std.
Error Sig. 95% Confidence Interval
Lower Bound Upper Bound
N0 N1 -1,60 0,25 0,00 -2,13 -1,06
N2 -1,34 0,25 0,00 -1,87 -0,80
N3 -2,59 0,25 0,00 -3,13 -2,06
N4 -2,70 0,25 0,00 -3,23 -2,16
N1 N0 1,60 0,25 0,00 1,06 2,13
N2 0,26 0,25 0,31 -0,27 0,80
N3 -0,99 0,25 0,00 -1,53 -0,46
N4 -1,10 0,25 0,00 -1,63 -0,56
N2 N0 1,34 0,25 0,00 0,80 1,87
N1 -0,26 0,25 0,31 -0,80 0,27
N3 -1,26 0,25 0,00 -1,79 -0,72
N4 -1,36 0,25 0,00 -1,90 -0,83
N3 N0 2,59 0,25 0,00 2,06 3,13
N1 0,99 0,25 0,00 0,46 1,53
N2 1,26 0,25 0,00 0,72 1,79
N4 -0,11 0,25 0,68 -0,64 0,43
N4 N0 2,70 0,25 0,00 2,16 3,23
N1 1,10 0,25 0,00 0,56 1,63

N2 1,36 0,25 0,00 0,83 1,90
N3 0,11 0,25 0,68 -0,43 0,64

• Sig. = Mức độ tin cậy
• 95% Confidence Interval = Khoảng tin cậy 95%
• Lower Bound = Khoảng tin cậy cận dưới

28
• Upper Bound = Khoảng tin cậy cận trên
Chúng ta có thể tính toán giá trị LSD bằng cách áp dụng công thức tính
LSD trong bảng 11 ở trên. Trong đó MSE là ước tính phương sai, M
1
là trung bình
quan sát của công thức thứ nhất, M
2
là trung bình quan sát của công thức thứ 2. n
1

là số lần lặp lại của công thức thứ nhất và n
2
là số lần lặp lại của công thức thứ 2.
Qua bảng 11 ta thấy rằng năng suất lúa ở các công thức phân bón N
1
đến
N
4
cao hơn so với năng suất lúa ở công thức đối chứng N
0
(P <0,05). Tương tự
như vậy ta có thể so sánh năng suất lúa của công thức N

1
so với đối chứng và các
công thức phân bón còn lại. Ta thấy rằng năng suất ở công thức phân bón N1 cao
hơn năng suất ở công thức phân bón N
0
(P <0,05), không sai khác năng suất ở
công thức N
2
(P>0,05) nhưng thấp hơn các công thức phân bón còn lại (P<0,05).
Ta có thể suy diễn tương tự cho các công thức phân bón N
2
, N
3
và N
4
.
Chúng ta hoàn toàn có thể sử dụng các kiểm tra post hoc khác như HSD với
cách nhận diện kết quả hoàn toàn tương tự.
Tóm lại, phân tích phương sai hoàn toàn có thể thực hiện một cách đơn
giản và có thể thực hiện đồng thời với các phân tích khác như phân tích thống kê
mô tả, phân tích post hoc.

BÀI 5. PHÂN TÍCH PHƯƠNG SAI CHO CÁC KIỂU THIẾT KẾ THÍ
NGHIỆM KHÁC NHAU
Trong phạm vi của bậc đại học chúng tôi đề cập đến cách phân tích số liệ
u
của 3 kiểu thiết kế thí nghiệm cơ bản: Thiết kế thí nghiệm ngẫu nhiên hoàn toàn
(CRD), thiết kế thí nghiệm theo khối ngẫu nhiên đầy đủ (RCB) và thiết kế thí
nghiệm hình vuông la tinh (LS hay LSD). Chúng tôi cũng chỉ giới thiệu phân tích
số liệu của thí nghiệm có một nhân tố. Bản chất của ví dụ 14 là một thiết kế thí

nghiệm kiểu CRD. Do vậy, trong phần này chúng tôi chỉ giới thiệu phân tích số
liệu c
ủa thiết kế thí nghiệm RCB và LSD. Chúng tôi cũng chỉ giới thiệu kỹ thuật
phân tích để kiểm tra giả thuyết H
0
, những nội dung đi kèm của phân tích số liệu
của các kiểu thiết kế thí nghiệm như phân tích thống kê mô tả và phân tích post
hoc, hoàn toàn tương tự như nội dung trong phần 4, như đã trình bày ở trên.

5.1. Nguyên tắc của phân tích số liệu của thiết kế thí nghiệm RCB và LSD
Nguyên tắc của hai kiểu thiết kế thí nghiệm này là có khống chế sự sai khác
ban đầu. Mục đích của khống chế sự sai khác ban
đầu là bóc tách ảnh hưởng của
những nguồn biến động đã biết ra khỏi nguồn biến động ngẫu nhiên. Trong thiết
kế thí nghiệm RCB đó chính là nguồn biến động tạo nên khối. Trong thiết kế thí
nghiệm LSD đó là nguồn biến động tạo nên yếu tố hàng và cột. Khi bóc tách các
nguồn biến động này ra khỏi biến động ngẫu nhiên thì chúng ta sẽ có kết luận
chính xác về ảnh hưởng c
ủa yếu tố thí nghiệm.

29
Nguyên tắc phân tích số liệu cũng như nhập số liệu của hai kiểu thiết kế thí
nghiệm này là xem xét yếu tố bị khống chế như là yếu tố thí nghiệm. Mọi ứng xử
đối với yếu tố bị khống chế hoàn toàn giống như yếu tố thí nghiệm. Chúng ta có
thể biết ảnh hưởng của yếu tố bị khống chế đến các biến ph
ụ thuộc, nhưng thông
thường chúng ta không quan tâm. Trong một số trường hợp chúng ta quan tâm, đó
là khi muốn so sánh hiệu quả của các kiểu thiết kế với nhau.

5.2. Phân tích số liệu từ thí nghiệm kiểu RCB

Ví dụ 15. Một nhóm nghiên cứu thí nghiệm ảnh hưởng của giống lúa đến
năng suất. Thí nghiệm được thiết kế theo kiểu RCB. Kết quả năng suất của các
giống lúa trong các khối khác nhau được th
ể hiện ở bảng 12. Hảy phân tích ảnh
hưởng của giống lúa đến năng suất.
Bảng 12. Ảnh hưởng của giống đến năng suất lúa trong một thí nghiệm
được thiết kế theo kiểu RCB
Khối Giống Năng suất Khối Giống Năng suất
K1 V1
2,373
K2 V4
5,630
K1 V1
4,076
K2 V4
7,007
K1 V1
7,254
K2 V4
7,735
K1 V2
4,007
K2 V5
3,276
K1 V2
5,630
K2 V5
5,340
K1 V2
7,053

K2 V5
5,080
K1 V3
2,620
K2 V6
3,724
K1 V3
4,676
K2 V6
2,822
K1 V3
7,666
K2 V6
2,706
K1 V4
2,726
K3 V1
4,384
K1 V4
4,838
K3 V1
4,889
K1 V4
6,881
K3 V1
8,582
K1 V5
4,447
K3 V2
5,001

K1 V5
5,549
K3 V2
7,177
K1 V5
6,880
K3 V2
6,297
K1 V6
2,572
K3 V3
5,621
K1 V6
3,896
K3 V3
7,019
K1 V6
1,556
K3 V3
8,611
K2 V1
3,958
K3 V4
3,821
K2 V1
6,431
K3 V4
4,816

30

K2 V1
6,808
K3 V4
6,667
K2 V2
5,795
K3 V5
4,582
K2 V2
7,334
K3 V5
6,011
K2 V2
8,284
K3 V5
6,076
K2 V3
4,508
K3 V6
3,326
K2 V3
6,672
K3 V6
4,425
K2 V3
7,328
K3 V6
3,214

Trước khi phân tích, chúng ta phải xác định mô hình phân tích. Với kiểu

thiết kế thí nghiệm RCB một nhân tố, thì mô hình phân tích có thể như sau:
y
ij
= µ + B
i
+ D
j
+ ε
ij
• y
ij
= Biến phụ thuộc
• µ = Trung bình quần thể
•
B
i
= Ảnh hưởng của khối

•
D
j
=Ảnh hưởng của biến độc lập (giống lúa)

•
ε
ij = Ảnh hưởng của ngẫu nhiên
Khi chúng ta đã rõ ràng về mô hình phân tích thì chúng ta có thể tiến hành
phân tích theo các bước như sau :
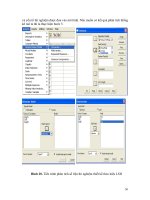
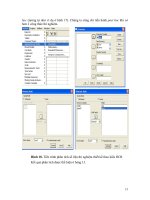
• Bước 1 : Nạp số liệu vào SPSS
• Bước 2: Vào trình ứng dụng General Linear Model-Univariate (hình

18.). Chúng ta sử dụng General Linear Model -Multivariate khi có nhiều biến phụ
thuộc. Chú ý biến phụ thuộc ở đây là biến định lượng.
• Bước 3 : Khai báo biến phụ thuộc (dependent variable) và biến độc
lập (fixed factors)(hình 18.). Chúng ta có thể thấy rằng cả yếu tố khối và yếu t
ố thí
nghiệm được đưa vào mô hình. Nếu chúng ta muốn có kết quả phân tích thống kê
mô tả thì ta thực hiện bước 5.
• Bước 4 : Khai báo mô hình phân tích (hình 18). Căn cứ vào mô hình
phân tích để khai báo mô hình. Nếu muốn xem ảnh hưởng đơn lẻ thì ta chọn từng
biến một. Nếu muốn xem ảnh hưởng của tương tác của các biến thì ta chọn đồng
thời các biến. Nếu chúng ta không thực hiện bước này thì máy tính sẽ thực hiện
theo chế độ mặc định. Chế độ mặc định là mô hình phân tích đầy đủ, có nghĩa bao
gồm cả ảnh hưởng đơn lẻ và ảnh hưởng tương tác.
• Bước 5 : Vào trình ứng dụng thống kê mô tả trong option (hoàn toàn
giống như ví dụ ở hình 16)
• Bước 6 : Nếu kết quả bác bỏ giả thuyết H
0
và chấp nhận H
A
thì phải
tiến hành phân tích post hoc. Nếu ta chấp nhận H
0
, thì không cần thực hiện post