Bài 8 hình học Tổng hợp các trường hợp đồng dạnh của tam giác vuông

07:02 PM
07:02 PM

GV:Tôn Nữ Bích Vân
TRƯỜNG THCS NGUYỄN KHUYẾN ĐÀ NẴNG
A
B
C
┐
M
N
07:03 PM
07:03 PM

•
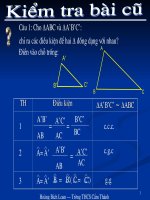
Nêu dấu hiệu đặc biệt nhận biết hai tam giác
vuông đồng dạng.
•
Nêu tỉ số hai đường cao, tỉ số diện tích hai tam
giác đồng dạng.
•
Cho tam giác ABC vuông tại A có AB = 6cm,
AC = 8cm. ∆A’B’C’ có diện tích 96 cm
2
, đồng
dạng với ∆ABC. Tính các cạnh của ∆A’B’C’
07:03 PM
07:03 PM

A
B

C
H
12,45
20,50
┐
a)Có ba cặp tam giác đồng dạng:
∆ABC ∽ ∆HBA (có góc B chung)
∆ABC ∽∆HAC (có góc C chung)
∆HBA ∽ ∆HAC (tính chất bắc cầu)
b) Áp dụng định lí Pitago ta có:
BC
2
= AB
2
+ AC
2
= 12,45
2
+ 20,50
2

∆ABC∽∆HBA⇒
∆ABC∽∆HAC⇒
HC= BC - HB = 23,98 – 6,46= 17,52(cm)
)cm(,,,BC 982350204512
22
=+=
AB
BC
HB

AB
=
)cm(,
,
,
BC
AB
HB 466
9823
4512
22
===⇒
AC
BC
HA
AB
=
)cm(,
,
,.,
BC
AC.AB
HA 6410
9823
50204512
===⇒
07:03 PM
07:03 PM

Gọi MN là chiều cao của thanh sắt, AB

là chiều cao của ống khói.
Hai tam giác vuông ABC và NMC có:
Góc C chung ⇒ ∆ABC ∽∆NMC


)m(,
,
,.,
CN
CA.MN
BA
BA
MN
CA
CN
8347
621
93612
===⇒
=⇒
A
B
C
┐
M
N
07:03 PM
07:03 PM

Cho tam giác ABC. Ba đường cao AD, BE, CF,

Cho tam giác ABC. Ba đường cao AD, BE, CF,
gọi H là trực tâm.
gọi H là trực tâm.
Chứng minh: HA.HD = HB. HE = HC.HF.
Chứng minh: HA.HD = HB. HE = HC.HF.
Cho tam giác ABC cân tại A, đường cao BH và
Cho tam giác ABC cân tại A, đường cao BH và
tam giác A’B’C’ cân tại A’, đường cao B’H’.
tam giác A’B’C’ cân tại A’, đường cao B’H’.
Biết AB = 12cm, BH = 9 cm, A’B’= 8cm, B’H’ =
Biết AB = 12cm, BH = 9 cm, A’B’= 8cm, B’H’ =
6cm. Tính tỉ số diện tích các tam giác B’H’C’và
6cm. Tính tỉ số diện tích các tam giác B’H’C’và
BHC.
BHC.
07:03 PM
07:03 PM

*
*
Làm bài tập 45,
Làm bài tập 45,
46,47,48/
46,47,48/


74
74
SBT.
SBT.

* Chuẩn bị tiết
* Chuẩn bị tiết
“
“
Ứng dụng thực
Ứng dụng thực
t
t
ế của
ế của


tam
tam
giác đồng dạng
giác đồng dạng
”
”
Từ một điểm D bất kỳ trên cạnh huyền AB
Từ một điểm D bất kỳ trên cạnh huyền AB
của tam giác vuông ABC, kẻ một đường
của tam giác vuông ABC, kẻ một đường
thẳng vuông góc với AB, cắt đường thẳng
thẳng vuông góc với AB, cắt đường thẳng
BC tại E và đường thẳng AC tại K.
BC tại E và đường thẳng AC tại K.
Chứng minh: AD.BD = DK.DE
Chứng minh: AD.BD = DK.DE
07:03 PM
07:03 PM

CHÚC CÁC EM HỌC TỐT
CHÚC CÁC EM HỌC TỐT