Bài tập lớn sức bền vật liệu

Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage1

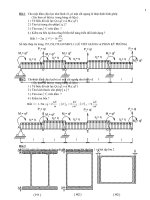
∗ SƠ ĐỒ A:
Cho q
0
=q= 3KN/m, a=1M
P
1
=2,2qa= 6,6 KN
P
2
=1,25P
1
= 8,25 KN
M= 2,2qa
2
= 6,6 KNm
Bài Làm:

q
P1=6,6KN
1 m
2,2 m
1 m
A
B
VB=1.8 kN
C
D

Q=9,6kN
M=6,6kNm
NZ
QY
MX
6,6kN
9,6kN
4,8kN
1,8kN
1,8kN
0
8,1kNm
4,8kN
4,26kN
6,6kNm
VC=14,4kN
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage2

∗ Xác định các phản lực tại gối C,D: dùng các PTCB

∑
z(
+
)= H
C
= 0

∑

Y(↑
+
)= V
B
+ V
C
– P
1
– Q = 0
 V
B
+ V
C
= P
1
+ Q= 2,2qa+3.2qa=5.4qa=16,2(kN)

∑
m
C
(
+
)=M – P
1
.a + Q(3,2a/2 – a ) – 3,2a.V
B
=0
 3,2qaV
B
=2,2qa

2
– 2,2qa
2
+ 1,92qa
2

 V
B
= 0,6qa=1,8(kN)  V
C
=16,2-1,8=14,4(kN)

A) Phương Pháp Mặt Cắt:
∗ Dùng mặt cắt (1-1) qua AC cách A đoạn Z
1
( 0 ≤Z
1
≤1m), xét phần bên
trái:




∑
z(
+
)= N
z1
=0

∑
Y(↓
+

)= Q
y1
+ P
1
+qz
1
=0
 Q
y1
= - (P
1
+qz
1
)= - qz
1
- 2,2qa
= -3z
1
– 6,6 (đtb1)
+ z
1
=0 : Q
Y1
= -6.6(kN)
+ z
1

=1 : Q
Y1
= -9,6(kN)

∑
m
O1
(
+
)=M
X1
+ P
1
z
1
+ qz
1
.z
1
/2=0
 M
X1
= -3z
1
2
/2 – 6,6z
1
( đường cong bậc2)
+ z
1

=0 : M
x1
=0
+ z
1
=1 : M
x1
=-8,1
O1
P1=6.6KN
1
1
q=3KN
M
x1
N
z1
Q
Y1
Z
1
Z
Y
A
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage3

Cực trị:
1

1
dMx
dZ
= -3z
1
-6,6=0 z
1
= -2,2
∉
[0,1]
∗ Dùng mặt cắt (2-2) qua CD cách C đoạn Z
1
( 0 ≤Z
2
≤2,2m), xét phần bên
phải:



∑
z(
+
)= N
z2
=0

∑
Y(↑
+
)= Q

y2
– qz
2
+V
B
=0
 Q
y2
= qz
2
– V
B
= 3z
2
-1,8 (đtb1)
+ z
2
=0 : Q
Y2
= -1.8(kN)
+ z
2
=2,2 : Q
Y2
= 4,8(kN)

∑
m
O2
(

+
)=M
X2
+ M + qz
2.
z
2
/2 – V
B
(1+z
2
) =0
 M
X2
= -3/2.z
2
2
+1,8z
2
– 4,8 ( đường cong bậc2)
+ z
2
=0 : M
x2
=-4,8 kNm
+ z
2
=2,2 : M
x2
=-8,1 kNm

Cực trị:
2
2
dMx
dZ
= -3z
2
+ 1,8=0  z
2
=0,6  M
cực trị
= -4,26 KNm
∗ Dùng mặt cắt (3-3) qua BD cách B đoạn Z
3
( 0 ≤Z
3
≤1m), xét phần bên
trái:
QY2
N
z2
VB=1,8KN
O
2
M=6,6KNm
M
x2
1mZ
2
q

Z
Y
2
2
B
D
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage4



∑
z(
+
)= N
z3
=0

∑
Y(↑
+
)=Q
Y3
+ V
B
= 0  Q
Y3
= -1,8 KN

∑
m
O3
(
+
)=M
X3
+M – V
B.
Z
3
=0  M
X3
= 1,8Z
3
– 6,6 (đtb1)
+ Z
3
=0 : M
x3
= -6,6 KNm
+ Z
3
=1 : M
x3
= -4,8 KNm
B) Kiểm Tra Lại Bằng Phương Pháp Liên Hệ Vi Phân:
∗ Đoạn AC: q phân bố = const (bậc0)  Q
Y1
(bậc 1), M

X1
(bậc 2)
Điểm A :
6,6
0
YA
XA
QKN
M
=−
⎧
⎨
=
⎩
 Điểm C:
Tr AC
YC YA q
Tr AC
X
CXAQY
QQS
M
MS
⎧
=−
⎪
⎨
=+
⎪
⎩


()
6,6 3.1 9,6( )
1
06,69,68,1()
2
Tr
YC
Tr
XC
QKN
M
KNm
⎧
=− − =−
⎪
⎨
=+ − − =−
⎪
⎩

∗ Đoạn CD: q phân bố= const (bậc0)  Q
Y2
(bậc 1), M
X2
(bậc2):
Vì tại C có lực tập trung V
C
nên phía bên phải C, Q

y
thay đổi
Điểm C phía bên phải:
9,6 9,6 14, 4 4,8( )
8,1( )
Ph
YC C
Ph
XC
QV KN
MKNm
⎧
=− + =− + =
⎪
⎨
=−
⎪
⎩

 Điểm D :
4,8 2,2.1.3 1,8( )
Ph CD
YD Y C q
QQS KN=−=− =−

VB=1,8KN
N
z3
Q
Y3

M
x3
O
3
M=6,6KNm
Z3
Z
Y
3
3
B
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage5

*Nhận Xét: Trên đoạn CD ta thấy Q
Y
thay đổi từ giá trị dương sang
âm   Q
y
=0  M
cưctri
tại vị trí Q
y
=0. Tìm vị trí cực trị:
Dựa vào ∆ đồng dạng:

1
2
4,8

1, 8
a
a
=

1
2
8
3
a
a
=
với a
1
+a
2
= 2,2 
1
2
8
.2,2
11
3
.2,2
11
a
a
⎧
=
⎪

⎪
⎨
⎪
=
⎪
⎩


1
83
8,1 (4,8. 1,8. ).2,2 4,8( )
11 11
2
Ph CD
XD XC QY
M
MS KNm= + =− + − =−

 Điểm D :
4,8 2,2.1.3 1,8( )
1
83
8,1 (4,8. 1,8. ).2,2 4,8( )
11 11
2
Ph CD
YD YC q
Ph CD
XD XC QY
QQS KN

M
MS KNm
⎧
=−=− =−
⎪
⎨
= + =− + − =−
⎪
⎩


∗ Đoạn DB : không có q phân bố  Q
Y3
= const, M
X3
(đường thẳng bậc 1)

1, 8( )
4,8 1,8.1 6,6( )
YB YD
DB
XB XD QY
QQ KN
M
M S KNm
==−
⎧
⎪
⎨
=+=−−=−

⎪
⎩


KẾT LUẬN : Cả hai phương pháp cùng cho kết quả giống nhau và sơ
đồ nội lực là như nhau.

Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage6

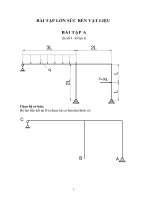
∗ SƠ ĐỐ B:
Cho: a=3M , b=0,9.a=2,7M , c=0,5a=1,5M
Q=q
0
=3 kN/m
P
1
=2,2qa=19,8 kN
P
2
=1,25P
1
=24,75 kN
M=2,2qa
2
=59,4 kNm
Bài Làm:

1,5m
3m
V
A
=20,25kN
H
A
=0
M
A
=28,44kNm
M=59,4kNm
P
1

=19,8kN
Q=0.45kN
q
2,7m
NZ
QY
20,25kN
0,45kN
28,44kNm
58,815kNm
0.585kNm
0,045
0
MX
A
B
C
D
0
0,45kN
0
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage7


A) Phương Pháp Mặt Cắt:
∗ Xác định các thành phần phản lực tại ngàm A:
()Z
+

→
∑
= H
A
=0
(
)
Y
+
↑
∑
= V
A
– P
1
– Q=0  V
A
= P
1
+ Q = 19,8 + 0,45 = 20,25 (kN)
m
∑
A
(
+
) = M
A
– M + P
1
.1,5 + Q.(2,7 +

1
3
.0,1.3) = 0
 M
A
= M – P
1
.1,5 – Q.(2,7 +
1
3
.0,1.3) = 28,44 (kNm)
∗ Dùng mặt cắt (1-1) qua đoạn AC, cách A khoảng Z
1
(0≤Z
1
≤1,5m), xét
phần bên trái:


()Z
+
→=
∑
N
Z1
= 0

(
)
Y

+
↓=
∑
Q
Y1
– V
A
= 0  Q
Y1
= V
A
= 20,25 (kN)

m
∑
O1
(
+
) = M
X1
– M
A
– V
A
.Z
1
= 0  M
X1
= 20,25.Z
1

+ 28,44 (đtb1)
+ Z
1
=0  M
X1
= 28,44 (kNm)
+ Z
2
= 1,5  M
X1
= 58,815 (kNm)
∗ Dùng mặt cắt (2-2) qua đoạn CD, cách A khoảng Z
1
(0≤Z
1
≤1,2m), xét
phần bên phải :

NZ1
QY1
MX1
V
A
=20,25 kNm
MA=28,44kNm
O1
1
1
Z
Y

Z1
A
Q
Y2
O
2
N
Z2
Q
Z
2
0,3
MX2
2
2
Y
Y
q
B
D
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage8

()Z
+
←=
∑
N
Z2

= 0

(
)
Y
+
↑=
∑
Q
Y2
– Q= 0  Q
Y2
= Q = 0.45 (kN)

m
∑
O2
(
+
) = M
X2
+ Q.(Z
2
+
1
3
.0,3) = 0  M
X2
= -0,45.Z
2

– 0,045 (đtb1)
+ Z
2
= 0 : M
X2
= -0,045 kNm
+ Z
2
= 1,2m: M
X2
= -0,585 kNm
∗ Dùng mặt cắt (3-3) qua đoạn BD, cách B khoảng Z
3
(0≤Z
3
≤0,3m), xét
phần bên phải :

Theo ∆ đồng dạng ta có:


0
33
0,3
()
q
qZ Z
=
 q(Z
3

) =
3
0,3
Z
.q
0
= 10.Z
3
 Q
3
=
1
2
.10.Z
3
. Z
3
= 5 .
2
3
Z


()Z
+
←=
∑
N
Z3
= 0

()
Y
+
↑=
∑
Q
Y3
– Q
3
=0  Q
Y3
= Q
3
=5.
2
3
Z

+ Z
3
= 0 : Q
Y3
= 0
+ Z
3
= 0.3 : Q
Y3
= 0.45 kN
Cực trị:

3
3
3
10 0
Y
dQ
Z
Z
==
 Z
3
=0  Q
Y3 cực trị
= 0

m
∑
O3
(+)

= M
X3
+ Q
3
.Z
3
.
1
3
Z

3
= 0  M
X3
= -
5
3
.
3
3
Z

+ Z
3
= 0 : M
X3
= 0
+ Z
3
= 0,3: M
X3
=-0,045
QY3
Nz3
Mx3
O3
Z3
q(Z3)
Y
Z
3

3
Q3
B
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage9

Cực trị :
2
3
3
3
5.
X
dM
Z
dZ
=−
<0  Z
3
: M
X3
là hàm nghịch biến, không có cực
trị.
B) Kiểm Tra Lại bằng Phương Pháp Liên Hệ Vi Phân:
Xét đoạn AC: không có q phân bố  Q
Y
= const, M
X
bậc 1

Điển A:
20,25
28,44
YA A
XA A
QV kN
M
MkNm
==
⎧
⎨
==
⎩

 điểm C :
020,25
28,44 20,25.1,5 58,815
tr
YC YA
Tr AC
XC XA QY
QQ kN
M
MS kNm
⎧
=+=
⎪
⎨
=+= + =
⎪

⎩

Xét đoạn CD: không có q phân bố  Q
Y
=const, M
X
bậc 1
Vì tại C có lực tập trung P
1,
và momen tập trung M nên phía bên phải
điểm C có bước nhảy:
Điểm C bên phải:
1
20,25 19,8 0,45
58,815 59,4 0,585
Ph Tr
YC YC
Ph Tr
XC XC
QQP kN
M
MM kNm
⎧
=−= − =
⎪
⎨
=−= −=−
⎪
⎩

Điểm D:
00,45
0,585 0,45.1,2 0,045
ph
YD YC
Ph CD
XD XC QY
QQ kN
M
MS kNm
⎧
=+=
⎪
⎨
=+=− + =−
⎪
⎩

Xét đoạn DB: q phân bố dạng tải tam giác (đường thẳng bậc 1)
 Q
Y
đường cong bậc 2, M
X
đường cong bậc 3.
Ta dễ dàng suy ra phương trình lực phân bố q tại từng điểm trên đoạn
DB: q(Z)=
10
3
.q.Z =10.Z (0≤Z≤0,3m)  phương trình của Q
Y

:
Q
Y
=
2
( ). 10. . 5qZ dZ ZdZ Z==
∫∫
(0≤Z≤0,3m)

Điểm B :
0,3
0
0,3
2
0
0,45 10. . 0
0,045 5. . 0
DB
YB YD q
DB
XB XD QY
QQS ZdZkN
M
MS ZdzkNm
⎧
=−= − =
⎪
⎪
⎨
⎪

=+=− + =
⎪
⎩
∫
∫


Kết Luận : Cả hai phương pháp cùng cho kết quả giống nhau và sơ
đồ nội lực là như nhau.




Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage10

SƠ ĐỒ C:
Cho a=2M
P
1
=2,2.3.2 = 13,2 kN
P
2
=1,25.P
1
= 16,5 kN
M=2,2.3.4 = 26,4 kNm
Bài làm:

0
0
36,6kNm
26,4kNm
26,4kNm
16,2kNm
20,4kNm
26,4kNm
M
X
6kN
13,2kN
Nz
0 kN
0 kN
E
A
D
C
B
2 m 2 m
2 m
2 m
V
A
=18,3kN
H
A
=6kN
Q=6kN

q
V
E
=5,1kN
M=26,4kNm
P1=13,2kN
18,3kN
5,1kN
6kN
0kN
13,2kN
Q
Y
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage11

Xác định phản lực tại các gối tựa:
()X
+
→=
∑
H
A
– Q=0  H
A
= Q = qa=6 kN
()Y
+
↑=

∑
V
A
– P
1
– V
E
= 0  V
A
– V
E
= P
1
=13,2 kN
m
∑
A
(
+
) = M – V
E
.4 – Q.
2
2
= 0  V
E
=
1
4
(M –Q)=

1
4
(26,4 – 6)=
5,1kN
 V
A
= 13,2 + V
E
= 13,2 + 5,1 = 18,3 kN
Phương Pháp Mặt Cắt:
Dùng mặt cắt (1-1) qua AB, cách A khoảng Z
1
(0≤Z
1
≤2m), xét phần
trái:


()Z
+
→=
∑
N
Z1
+ H
A
= 0  N
Z1
= - H
A

= -6 kN
()
Y
+
↓=
∑
Q
Y1
– V
A
= 0  Q
Y1
= V
A
= 18,3 kN
m
∑
O1
= M
X1
– V
A
.Z
1
=0  M
X1
= 18,3.Z
1
(đường thẳng bậc 1)
+ Z

1
=0  M
X1
= 0 kNm
+ Z
1
=2  M
X1
= 36,6 kNm
Dùng mặt cắt (2-2) qua BC, cách A khoảng Z
1
(0≤Z
2
≤2m), xét phần
bên dưới điểm C:
Z
1
V
A
=18,3 kN
H
A
=6kN
Q
Y1
N
Z1
1
1
M

X1
O
1
A
Z
Y
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage12


()Z
+
↑=
∑
N
Z2
– P
1
= 0  N
Z2
= P
1
= 13,2 kN
()Y
+
→=
∑
Q
Y2

– q.Z
2
=0  Q
Y2
= q.Z
2
= 3. Z
2
(đường thẳnng bậc 1)
m
∑
O2
(
+
) = M
X2
+Q.Z
2.
2
2
Z

- 13,2.2 = 0
 M
X2
= -
3
2
Z
2

2
+ 26,4 (đường cong bậc 2)
+ Z
2
= 0  M
X2
= 26,4 (kNm)
+ Z
2
= 2  M
X2
= 20,4 (kNm)
Cực trị:
2
2
2
3. 0
X
dM
Z
dZ
=− <
V Z
2
 hàm số luôn giảm
Dùng mặt cắt (3-3) qua CD, cách D khoảng Z
3
(0≤Z
3
≤2m), xét phần

bên trái:


()Z
+
→=
∑
N
Z3
= 0
()
Y
+
↓=
∑
Q
Y3
+ P
1
= 0  Q
Y3
= -P
1
= -13,2 (kNm) = const
P1=13,2kN
D
Q
2
C
Z

2
N
Z2
Q
Y2
M
X2
O2
q
Z
Y
N
Z3
Q
Y3
D
O
3
M
X3
Z3
P1=13,2kN
Z
Y
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage13

m
∑

O3
(
+
) = M
X3
- 13,2.Z
3
= 0  M
X3
= 13,2.Z
3
(đường thẳng bậc 1)
+ Z
3
= 0 : M
X3
= 0 kNm
+ Z
3
= 2 : M
X3
= 26,4 (kNm)
Dùng mặt cắt (4-4) qua BE, cách E khoảng Z
4
(0≤Z
4
≤2m), xét phần
bên phải :

()Z

+
←
=
∑
N
Z4
= 0
()
Y
+
↑=
∑
Q
Y4
- V
E
= 0  Q
Y4
= V
E
= 5,1 kN
m
∑
O4
= M
X4
– M +V
E
.Z
4

= 0  M
X4
= M – 5,1.Z
4
(đường thẳnng bậc1)
+ Z
4
= 0 : M
X4
= 26,4 (kNm)
+ Z
4
= 2 : M
X4
= 16,2 (kNm)
Kiểm Tra Bằng Phương Pháp Vi Phân:
Đoạn AB : không có q phân bố  Q
Y1
bậc 0; M
X1
bậc 1
Điểm A :
18,3
0
YA A
XA
QV kN
MkNm
==
⎧

⎨
=
⎩

 điểm B phía bên trái:
18,3
018,3.2 36,6
Tr
YB YA
Tr AB
XB XA QY
QQ kN
M
MS kNm
⎧
==
⎪
⎨
=+=+ =
⎪
⎩

Xét đoạn BC : có q = const  Q
Y2
bậc 1 ; M
X2
bậc 2
Tính phản lực tại điểm B phía bên dưới :
O
4

Q
Y4
N
Z4
M
X4
M=26,4kNm
E
V
E
=5,1kN
Z
4
Z
Y
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage14

- Dời lực H
A
về điểm B ta được :
6
duoi
YB A
QHkN==

- Momen tại điểm B (bên dưới) lien quan đến các lực do thanh BC,
CD gây ra tức là lực phân bố q (trên thanh BC) và lực P
1

(trên
thanh CD)

12
2
.2 . 13,2.2 6 20,4
2
duoi
XB
M
PQ kNm=− = −=

Vậy điểm B ở phía dưới:
12
6
2
.2 . 13,2.2 6 20,4
2
duoi
YB A
duoi
XB
QHkN
M
PQ kNm
⎧
==
⎪
⎨
=− = −=

⎪
⎩

 điểm C:
63.2 0
1
20,4 .6.2 26,4
2
tren duoi BC
YC YB q
Tren duoi BC
XC XB QY
QQS kN
M
MS kNm
⎧
=−=−=
⎪
⎨
=+=+=
⎪
⎩

Xét đoạn CD : không có q phân bố  Q
Y3
=const; M
X3
(đường
thẳng bậc1)
Điểm C bên trái :

Kiểm Tra Cân Bằng Tại Các Nút :
Tại nút B:
()X
+
→=
∑
N
Z1
– Q
Y
= 6 – 6 = 0
kN
()Y
+
↑=
∑
Q
Y1
– Q
Y4
– N
Z2
= 18,3 –
5,1 – 13,2 =0 kN
m
∑
B
(
+
) = M

X1
– M
X4
– M
X2
=
36,6 – 16,2 – 20,4 = 0 kNm
Vậy tại nút B cân bằng

Tại nút C:
0X =
∑

()Y
+
↑=
∑
N
Z2
– Q
Y3
= 13,2 – 13,2 = 0
m
∑
C
(
+
)=M
X2
– M

X3
=26,4 – 26,4=0
Vậy tại nút C cân bằng





C
N
Z2
=13,2
M
X2
=26,4
Q
Y3
=13,2
M
X3
=26,4
QY1=18,3
NZ1=6
N
Z2
=13,2
Q
Y4
=5,1
Q

Y2=
6
MX1=36,6
MX4=16,2
MX2=20,4
B
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage15


SƠ ĐỒ D:
Cho :
a=2M; q
0
= q = 3kn/m
P
1
= 13,2kN
P
2
= 12,5.13,2 = 16,5 kN
M = 26,4 kNm
R = 1M
Bài làm:


A
B
P1=13,2kN

P2=16,5kN
M=26,4kNm
HA=21kN
O
VA=39,6kN
VB=2,33kN
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage16

Sơ đồ nội lực:
41,93kN
0 kN
44,82 kN
NZ
0 kN
41,93 kN
41,93 kN
0 kN
QY
0 KNm
3,25
29,65kNm
41,93 kNm
0 kNm
0 kNm
MX
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage17



Xác định phản lực tại các gối tựa:
()X
+
→=
∑
H
A
– P
1
.sinα – P
2
.cosα = 0  H
A
= P
1
.sinα + P
2
.cosα = 13,2.
2
2
+ 16,5.
2
2
= 21kN
()Y
+
↓=
∑

V
A
- V
B
– P
1
.cosα + P
2.
sinα = 0
 V
B
– V
A
= 16,5.
2
2
- 13,2.
2
2
= 2,33
m
∑
O
(
+
) = M – V
A
.R + P
1
.R = 0  V

A
=
M
R
+ P
1
= 26,4 + 13,2 = 39,6 kN
 V
B
= 39,6 + 2,33 = 41,93 kN
Phương Pháp Mặt Cắt :
Xét đoạn AC:
()Z
+
∑
/
= N
Z1
– H
A
.sinα
1
– V
A
.cosα
1
= 0
 N
Z1
= 21.sinα

1
+ 39,6.cosα
1
(0≤α
1
≤45
0
)
()Y
+
=
∑
2
Q
Y1
– H
A
. cosα
1
+ V
A
. Sinα
1
= 0
 Q
Y1
= 21.Cosα
1
– V
A

.Sinα
1

m
∑
O
(
+
) = M
X1
+ H
A
.R. sinα
1
– V
A
.(R – R.cosα
1
) = 0
 M
X1
= -H
A
.R.sinα
1
– V
A
.cosα
1
+ V

A
= -21.sinα
1
–
39,6.cosα
1
+ 39,6
Tìm vị trí cực trị của N
Z1
và M
X1


1Z
dN
d
ϕ
= 21.cosα
1
– 39,6.sinα
1
= Q
Y1

1X
dM
d
ϕ
= -21.cosα
1

+ 39,6.sinα
1
= -Q
Y1

Q
Y1
= 0  21.cosα
1
– 39,6.sinα
1
= 0  tgα
1
=
21
39,6
≈0,53  α
1
≈27,93
0
[0;45
0
]
N
Z1
và M
X1
đạt cực trị tại vị trí α
1
≈27,93

0

Bảng giá trị:
A
HA=21kN
VA=39,6kN
NZ1
QY1
MX1
O
a1
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage18

0 10 20 27.93 30 40 45
NZ1 39.60 42.64 44.39 44.82 44.79 43.83 42.85
QY1 21.00 13.80 6.19 0 -1.61 -9.37 -13.15
MX1 0 -3.04 -4.79 -5.22 -5.19 -4.23 -3.25
Xét đoạn BC α
2
N
Z2
= -V
B
.sinα
2
=-41,93.sinα
2

Q
Y2
= V
B
.cosα
2
=41,93.cosα
2

M
X 2
= V
B
.sinα
2

Tìm vị trí cực trị của N
Z2
và M
X 2

2
2
Z
dN
d
ϕ
=
-V
B

.cosα
2
= -Q
Y2
2
2
X
dM
d
ϕ
=
V
B
.cosα
2
= Q
Y2

Q
Y2
= 0  cosα
2
= 0  α
2
=90
0
 [0;225
0
]
Bảng giá trị:

0 30 60 90 120 135 150 180 210 225
NZ2 0 -20.97 -36.31 -41.93 -36.31 -29.65 -20.97 0 20.97 29.65
QY2 41.93 36.31 20.97 0.00 -20.97 -29.65 -36.31 -41.93 -36.31 -29.65
MX2 0 20.97 36.31 41.93 36.31 29.65 20.97 0 -20.97 -29.65







B
VB=2,33kN
QY2
MX2
NZ2
O
a2
Y
Z
Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage19


Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage20


Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage21


Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage22


Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage23



Bài Tập Lớn Sức Bền Vật Liệu

TRẦN SONG ÁNHPage24
