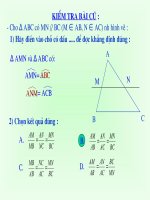Tiết 42 (Khái niệm tam giac đồng dạng)

Hãy nhận xét về hình dạng và kích th ớc của
các hình trong mỗi nhóm.
Nhóm 1 Nhóm 2 Nhóm 3

3
2,5
2
B'
A'
C'
6
5
4
B
A
C
TiÕt 42 §4. Kh¸i niÖm hai tam gi¸c ®ång d¹ng
1. Tam gi¸c ®ång d¹ng
?
?
1
1
' ' 2 1 ' ' 3 1 ' ' 2,5 1
; ;
4 2 6 2 5 2
1' ' ' ' ' '
2
A B B C C A
A
A B B C C A

AB BC CA
B BC CA
= = = = =
= =
=
⇒ =
µ
µ
µ
µ
µ
µ
' ; ' ; 'A A B B C C= = =
§Þnh nghÜa: (SGK/70)
∆ A’B’C’ vµ ∆ ABC cã

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
1. Tam giác đồng dạng
à
à
à
à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)
= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC

S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
Bài 1: Cho PQR MNE
S

Từ định nghĩa tam giác đồng
dạng ta có điều gì?
à
ả
;P M=
à
ả
;Q N=
à
à
R E=
Có PQR MNE
S

PQ QR RP
ME NE EN
= =
b) Tính chất:

ABC đồng dạng với ABC nếu:

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
1. Tam giác đồng dạng
à
à
à
à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)
= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC
S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
b) Tính chất:
?
?
2
2

A
B
C
A
B
C
1)
Mối quan hệ về
góc
Tỉ lệ giữa các
cạnh t ơng ứng
à
à
à
à
à
à
' ; ' ;
'
A A B B
C C
= =
=
1= = =
A'B' B'C' C'A'
AB BC CA
Kết luận:
Tỉ số đồng dạng:
k=1
à

à
à
à
à
à
' ; ' ; 'A A B B C C= = =
k= = =
A'B' B'C' C'A'
AB BC CA
1
k
= = =
AB BC CA
A'B' B'C' C'A'
Vậy ABC ABC theo tỉ
số đồng dạng là 1/k.
S

ABC ABC
S

2) ABC ABC theo tỉ số k
S

ABC đồng dạng với ABC nếu:

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
à
à
à

à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)
ABC đồng dạng với ABC nếu:
= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC
S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
b) Tính chất:
SGK/70
2. Định lí
?
?
3
3
NM
B C
A
a

(Hệ quả định lí
Ta-lét)
ã
ã
AMN ABC=
ã
ã
ANM ACB=
ã
BAC
(đồng vị)
(đồng vị)
(chung)
AM MN NA
AB BC CA
= =
AMN
S
ABC
1. Tam giác đồng dạng

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
à
à
à
à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)

ABC đồng dạng với ABC nếu:
= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC
S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
b) Tính chất:
SGK/70
2. Định lí
NM
B C
A
a
(Hệ quả định lí
Ta-lét)
ã
ã
AMN ABC=
ã
ã
ANM ACB=
ã

BAC
(đồng vị)
(đồng vị)
(chung)
AM MN NA
AB BC CA
= =
AMN
S
ABC
: SGK/71
GT
KL
ABC có MN//BC (MAB;NAB)
AMN
S
ABC
Chứng minh: SGK/71
1. Tam giác đồng dạng

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
à
à
à
à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)
ABC đồng dạng với ABC nếu:

= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC
S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
b) Tính chất:
SGK/70
2. Định lí : SGK/71
GT
KL
ABC có MN//BC (MAB;NAB)
AMN
S
ABC
Chứng minh: SGK/71
1. Tam giác đồng dạng
Chú ý: SGK/71
A
B
C
M N a
A

B
C
M
N
a

Bµi tËp


Chọn câu trả lời đúng nhất:
Chọn câu trả lời đúng nhất:


Cho
Cho
∆
∆
ABC. Từ điểm M trên cạnh AB với
ABC. Từ điểm M trên cạnh AB với


, kẻ các tia song song với AC và BC,
, kẻ các tia song song với AC và BC,
chúng cắt BC và AC lần lượt tại D và N.
chúng cắt BC và AC lần lượt tại D và N.


Số cặp
Số cặp
tam giác đồng dạng có trong hình vẽ là:

tam giác đồng dạng có trong hình vẽ là:




a/ 1 cặp
a/ 1 cặp


b/ 2 cặp
b/ 2 cặp


c/ 3 cặp
c/ 3 cặp


d/ 4 cặp
d/ 4 cặp
1
3
AM MB=
A
B
C
L
N
M
D

Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
à
à
à
à
à
à
' ; ' ; 'A A B B C C= = =
Định nghĩa: (SGK/70)
ABC đồng dạng với ABC nếu:
= =
A'B' B'C' C'A'
AB BC CA
* Kí hiệu: ABC ABC
S

' ' ' ' ' '
*
A B B C C A
AB BC CA
= =
k=
(k: Tỉ số đồng dạng)
b) Tính chất:
SGK/70
2. Định lí : SGK/71
GT
KL
ABC có MN//BC (MAB;NAC)
AMN

S
ABC
Chứng minh: SGK/71
1. Tam giác đồng dạng
Tiết 42 Đ4. Khái niệm hai tam giác đồng dạng
H ớng dẫn về nhà
+ Học thuộc định nghĩa, tính chất,
định lí 2 tam giác đồng dạng.
+ Bài tập 23; 24 (SGK/72).