Bài 1. Hàm số lượng giác

O
+
-1
-1
1
1
B
A
A’
B’
M
P
K
α
H
x
y
T
S
HAØM SOÙÁ LÖÔÏNG GIAÙC
- π - π/2
π/2 π
1
-1
y
x
0
NỘI DUNG BÀI HỌC (4 Tiết)
I - ĐỊNH NGHĨA HÀM SỐ LƯỢNG GIÁC.
II - TÍNH TUẦN HOÀN CỦA HÀM SỐ LƯỢNG GIÁC .
III - SỰ BIẾN THIÊN CỦA HÀM SỐ LƯỢNG GIÁC .

IV - LUYỆN TẬP .
I – ĐỊNH NGHĨA :
BẢNG GIÁ TRỊ LƯỢNG GIÁC
CỦA CÁC CUNG ĐẶC BIỆT :

Nhắc lại bảng giá trị lượng giác
của một cung đặc biệt ?
CUNG
x
GTLG
0
sinx
0
1
cosx 1 0
tanx 0 1 ||
cotx
||
1 0
π
6
π
4
π
3
π
2
1
2
2

2
3
2
3
2
2
2
1
2
3
3
3
3
3
3
c) Sin2 ≈ 0,91
Cos2 ≈- 0,42

Dùng máy tính bỏ túi ,tính :
sinx, cosx. Với :
a)x = π/4
b)x = π/6
c) x = 2
TRẢ LỜI :
a) sin π/4 ≈ 0,71
COS π/4 ≈ 0,71
b) sin π/6 =0,5
COS π/6 ≈ 0,87
y
x

y
x

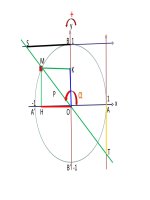
Trên đường tròn lượng giác,với
điểm gốc A,hãy xác định các điểm M
mà số đo tương ứng là:
a) π/4
b) π/6
1) HÀM SỐ SIN VÀ HÀM SỐ côsin:
y
x
0
sinx
M
a)y = sin x :
được gọi là hàm số sin, kí hiệu là y = sinx
Tập xác định của hàm số y = sinx là R.
Qui tắc tương ứng mỗi x∈R với số thực sinx
x
y
sinx
sin : R R
x l y = sinx
1)HÀM SỐ COSIN VÀ HÀM SỐ SIN :
b)y = cos x :
được gọi là hàm số cos, kí hiệu là y = cosx
Tập xác định của hàm số y = cosx là R.
Qui tắc tương ứng mỗi x∈R với số thực cosx
cos : R R
x l y = cosx

x
y
cosx
y
x
0
cosx
M
Ví dụ : Tìm tập xác của mỗi hàm số sau :
) 2 sinxa y = −
Trả lời :
a)Do nên tập xác định của hàm số là D = R
2 sinx 0− >
1 c os
)
sinx
x
b y
−
=
b) Để hs xác định thì sinx 0, nên tập xác định của
hàm số là D = R\ { kπ; k∈Z }
≠
1 sinx
)
1 cos
c y
x
−
=

+
c) Do 1- sinx 0 và 1+cosx 0, nên hs xác định thì
1+cosx > 0, nên tập xác định của hàm số là
D = R \ {( 2k+1)π; k∈Z }
≥
≥
2)HÀM SỐ TANG VÀ HÀM SỐ COTANG :
a) y = tanx :
Tập xác định : D = R\ { π/2 + kπ; k∈Z }
.(
sin
cos
cos
0)
x
y x
x
=
≠
b)y = cotx :
Tập xác định : D = R\ { kπ; k∈Z }
.(
cos
sin 0)
sin
x
y x
x
= ≠
Hàm số tang là hàm số được xác định bởi công thức :

Hàm số côtang là hàm số được xác định bởi công thức :
xO
B’
A
B
A’
y
M
x
-x
M’
Hãy so sánh các giá trị của sinx và sin(-x),
cosx và cos(-x)
Trả lời :
Sinx = - sin(-x)
Cosx = cos(-x)
Nhận xét :
Hàm số y=sinx là hs lẻ,
hàm số y=cosx là hs chẵn,
suy các hs y=tanx
và y = cotx đều là hs lẻ.
II- TÍNH TUẦN HOÀN CỦA HSLG:
Ta nói chu kì của các hàm số : y = sinx là 2π
Tìm những số T sao cho f(x+T)=f(x) với mọi x
thuộc tập xác định của hàm số sau :
a) f(x)=Sinx
Trả lời :
Sin(x+ 2π)=sinx
Sin(x- 2π)=sinx
Sin(x+ 4π)=sinx

Tương tự chu kì của các hàm số : y = Cosx là 2π
tan(x+ π)=tanx
tan(x - π)=tanx
tan(x+ 2π)=tanx
Ta nói chu kì của các hàm số : y = tanx là π
Tương tự chu kì của các hàm số : y = cotx là π
b) f(x) =tanx
1) Hàm số y = sinx:
III- SỰ BIẾN THIÊN CỦA HÀM SỐ LƯỢNG GIÁC:
a)Sự biến thiên của đồ thị y = sinx
trên đoạn [0;π] :
∀
∀x
1
,x
2
∈(0;π/2); x
1
<x
2
ta có :sinx
1
<sinx
2
∀
∀x
1
,x
2
∈(π /2; π); x

1
<x
2
ta có : sinx
1
>sinx
2
Vậy, hàm số y = sinx :
+ đồng biến trên khoảng (0;π/2).
+ nghịch biến trên khoảng (π/2; π).
y
y
0
0
x
x
x
0 π/2 π
y = sinx 1
0 0
π/2
π
1
1) Hàm số y = sinx:
y
x
0
- π - π/2
π/2 π
1

-1
Trên đoạn [ -π; π], đồ thị đi qua các điểm :
(0;0); (π/2;1); (-π/2;-1); (-π;0);(π;0) .
y
x
0

Tập xác định D = R

Hàm số lẻ

Hàm số tuần hoàn , chu kì T = 2π

Tập giá trị :đoạn [ - 1; 1]
- π - π/2
π/2 π
1
-1
2) Hàm số y = cosx:

Tập xác định D = R

Hàm số chẵn

Tuần hoàn , chu kì T = 2π

Tập giá trị :đoạn [ - 1; 1]
Lưu ý : sin (x+
π
/2 ) = cosx

Từ đó ta có đồ thị hàm số cosx
như sau:
y
x0
4
π
2
π
3
4
π
3
4
π
−
π
-π
2
π
−
3) Hàm số y = tanx:

Tập xác định: D = R \ { π/2 +kπ; k∈Z }

Hàm số lẻ

Tuần hoàn , chu kì T = π

Tập giá trị : R


Tăng trên các khoảng :
(-π/2 + kπ; π/2 + kπ)
x
π
2
π
−
π
2
−
π
−
3π
2
4) Hàm số y = cotx:

Tập xác định : D = R \ { kπ; k∈Z }

Hàm số lẻ

Tuần hoàn , chu kì T = π

Tập giá trị : R
x
CỦNG CỐ BÀI
•
1) Khái niệm các hàm số lượng giác
•
2) Nắm các tính chất của 4 HSLG :
chẵn, lẻ; tuần hoàn; đơn điệu .

•
3) Nhận dạng đồ thị của từng HSLG .
Ví dụ 1: Tập xác định của hàm số:
A. R B. R\{π/4+kπ,k∈Z}
C. [ -1;1] D.Một đáp số khác
y =
2sinx + cosx
sin(x - π/4)
B
CỦNG CỐ BÀI
•
1) Khái niệm các hàm số lượng giác
•
2) Nắm các tính chất của 4 HSLG :
chẵn, lẻ; tuần hoàn; đơn điệu .
•
3) Nhận dạng đồ thị của từng HSLG .
Ví dụ2 : Tập giá trị của hàm số
y = 5sin(3x + 2) – 2 laø :
A. [ - 1; 1] B.( -7;7)
C. [ -7;-2] D.[- 7; 3]
D