bai 1:hàm số lượng giác

Gv : ngun thÞ h êng
Ngày soạn : 25/ 08/ 2008: tiÕt:1+2 tn:1
§ 1 CÁC HÀM SỐ LƯNG GIÁC
I. Mục đích yêu cầu:
1. Kiến thức trọng tâm:
-Nắm đựợc đònh nghóa hàm số sin, và hàm số cosin dẫn đến hàm số tan, cot, các
tính chất của hàm số lượng giác.
2. Kỷ năng cơ bản :.
- Kỹ năng xác đònh tập xác đònh, tập giá trò, tính chẵn lẻ, tính tuần hoàn, chu kỳ
của các hàm số lượng giác.
3. Giáo dục tư tưởng :
Phát triển tư duy logic, chính xác, tính cần cù trong học tập.
II. Phương pháp dạy học: Dùng phương pháp gợi mở vấn đáp thông qua các hoạt
động điều khiển tư duy, đan xen hoạt động nhóm.
III. Chuẩn bò của thầy và trò:
- Thầy : Xem SGK , tài liệu tham khảo & soạn giáo án
- Trò : Xem trước bài mới
IV. Tiến trình bài học và các hoạt động.
1. Các hoạt động.
HĐ 1: ĐN hàm số y=sinx và y=cosx.
HĐ 2: Đònh nghóa hàm số y= tanx và y=cotx.
HĐ 3: Bài tập rèn luyện, củng cố kiến thức.
HĐ 4: Tính chẵn, lẻ của các hàm số lượng giác.
HĐ 5: Tính tuần hoàn của các hàm số lượng giác.
HĐ 6: Trắc nghiệm kiến thức củng cố.
2. Tiến trình bài học.
a) Ổn đònh lớp : Só số, tác phong học sinh ( 01 phút)
b) Kiểm tra bài cũ : ( Không )
c) Bµi míi.
Ho¹t ®éng häc sinh Ho¹t ®éng gi¸o viªn
- Với các giá trò x dùng máy tính tính

sinx và cosx tương ứng ta có một giá
trò sinx và cosx
-Với mỗi giá trò x ta xác đònh 1 điểm
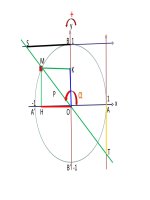
Hoạt đông 1. Đònh nghóa hàm số y=sin x và
y=cosx.
- Làm hoạt động 1 sgk.
-với mỗi giá trò của x tương ứng, có bao
ngọn M trên đường tròn lượng giác
sao cho số đo cung lượng giác AM
bằng x, tương ứng 1 giá trò sin x và
cosx.
-Với 1 giá trò x ta có tương ứng 1 giá
trò sinx, cosx.
-Quy tắc đặt tương ứng:
sin:
sinx y x
→
=
¡ ¡
a
gọi là hàm số
y=sinx.
Tập xác đònh của hàm số là
¡
.
-Tương tự hàm số y=cosx coa tập xác
đònh
¡
.
-Hàm số y=tanx là hàm số xác đònh

bởi công thức y=
sin
, cos 0.
cos
x
x
x
≠
-Tập xác đònh của hàm số y= tanx là
D=
}
,
2
x x k k
π
π

∈ ≠ + ∈


¡ ¢
.
-Hàm số y=tana
0
x xác đònh khi :
a
0
x
, .
2

k k
π
π
≠ + ∈ ¢
-Hàm số y= cotx là hàm số xác đònh
bởi công thức : y=
cos
,sin 0.
sin
x
x
x
≠
-Tập xác đònh của hàm số là :
D=
{ }
,x x k k
π
∈ ≠ ∈¡ ¢
-Hàm số y=cota
0
x xác đònh khi
a
0
x
, .k k
π
≠ ∈ ¢
.

a. y= tan(2x-
3
π
).
-Biểu thức xác đònh khi :
2 ,
3 2
x k k
π π
π
− ≠ + ∈ ¢
, giải ra ta được
x
5
, .
12 2
k k
π π
≠ + ∈ ¢
. Tập xác đònh.
b. y=
2 cos 1
sin 2
x
x
−
-Biểu thức xác đònh khi sin2x
≠
0,
giải ra ta có

2 , .
2
x k x k k
π
π
≠ ⇔ ≠ ∈ ¢
nhiêu giá trò sinx?
-Trên đường tròn lượng giác tìm điểm ngọn
M sao cho số đo cung lg AM bằng x, tương
ứng xác đònh sinx và cosx.
-Biểu diễn x trên trục hoành và tương ứng
sinx trên trục tung?
-Giáo viên hướng dẫn học sinh nêu đònh
nghóa?
-Tương tự đònh nghóa hàm số y=cosx
-Tập cxác đònh cuả hàm số y=sinx và y=
cosx?
-Tương tự như hàm số với các biến số thực
đã được học.
Hoạt đông 2. ĐN hàm số y= tanx và hàm số
y=cotx.
-Đònh nghóa hàm số y= tanx theo hàm số
y=sinx và y= cosx theo công thức đã học.
- Tương tự đònh ngiã hàm số y-=cotx theo 2
hàm số y=sinx và y=cosx theo công thức
lượng giác.
-Tập xác đònh của hàm số y=tanx.
-Tập xác đònh của hàm số y= cotx.
- Cách tìm tập xác đònh của hàm số y=
tana

0
x và cota
0
x?
Hoạt động 3. Tìm tập xác đònh của các hàm
số sau:
a. y= tan(2x-
3
π
).
b. y=
2 cos 1
sin 2
x
x
−
-Hàm só tanx xác đònh khi nào?
-y= tanu xác đònh khi nào?
-Gọi học sinh lên giải.
-Tập xác đònh?
-Biểu thức p(x)/q(x) xác đònh khi nào?
-Sin2x
0≠
khi nào?
-Gọi học sinh lên giải.
Tập xác đònh.
-Theo công thức hai cung đốu nhau ta
có: sin(-x) =-sinx; cos(-x) = cosx
tan(-x) =-tanx và cot(-x) =- cotx.
-Tập xác đònh của 4 hàm số lượng

giác thỏa nmãn điều kiện hàm số
chẵn, lẻ.
- hàm số y= cosx là hàm số chẵn.
-ham số y= sinx, y=tanx, y= cotx là
các hàm số lẻ.
-Hàm số y=sinax, y= tanax, y=cotax
cũng là các hàm số lẻ.
- hàm số y= cosax là hàm số chẵn.
-Hàm số thỏa mãn công thức
f(x+T)= f(x) là hàm số tuần hoàn.
-Đối với hàm số y= sinx ta có :
sin(x+k
2
π
) = sinx suy ra T= k
2
π
là số
thực T cần tìm. Có vô số các giá trò T
như thế.
-Đối với hàm số y = tanx ta có :
tan(x+k
π
)= tanx suy ra số thực T =k
π
là giá trò cần tìm. Có vô số các giá trò
T như thế.
-ta tìm số thực T>0 nhỏ nhất dựa vào
các giá trò k tương ứng ta có k=1 thì T
là giá trò cần tìm.

-T=2
π
và T=
π
là 2 giá trò thỏa mãn
tương ứng với 2 hàm số y=sinx và y=
tanx.
-Nếu hàm số y= sin(ax+b) thì chu kỳ
của hàm số là : T=2
π
/a, tương tự hàm
số y=tan(ax+b) có chu ky là T=
π
/a.
-Tập xác đònh của hàm số.
Tiết 2
Hoạt động 4. Tính chẵn, lẻ của các hàm số
lượng giác.
-So sánh các giá trò lượng giác sau:
sin(-x) và sinx; cos(-x) và cosx
tan(-x) và tanx; cot(-x) và cotx.
-Nhắc lại đònh nghóa hàm số chẵn, lẻ?
-Tập xác đònh của các hàm số lượng giác có
thỏa mãn điều kiện của hàm số chẵn, lẻ
chưa?
-Nhận xét về tính chẵn, lẻ của hàm số
y=cosx?
-Hàm số y= sinx, y=tanx, y= cotx có cùng
tính chất?
-Các hàm số y= sinax, cosax, tanax, cotax

có cùng tính chất như hàm số sinx, cosx,
tanx, cotx hay không?
Hoạt động 5. Tính tuần hoàn của hàm số
lượng giác.
- Cho hàm số y=f(x), tìm các số thực T sao
cho f(x+T)= f(x)?
- Với f(x) = sinx, f(x)= tanx?
-Các tính chất của các công thức lượng
giác?
-Ta có công thức sin(x+k
2
π
) = sinx => số
thực T là các số nào?
-Tương tự cho tanx ta có: tan(x+k
π
)= tanx.
=> số thực T ?
-Trong các số thực T trong biểu thức sinx
tìm số thực T>0 nhỏ nhất?.
-Tương tự trong các số thực T trong biểu
thức tanx, tìm số thực T>0 nhỏ nhất?
-Số thực T>0 nhỏ nhất ứng với giá trò k
bằng bao nhiêu?
-hàm số cho bởi công thức y= f
1
(x) +
f
2
(x)có chu kỳ lần lượt là T

1
và T
2
thì
chu kỳ của hàm số
làT=BSCNN(T
1
,T
2
).
6. T×m chu kú cđa hµm s« y=sin6x
A. T=
π
B. T=
π
/3
C. T=
π
/2 D. T=2
π

7. T×m chu kú cđa hµm sè y= sin
2
x

A. T=4
π
B. T=
π

C. T=
π
/2 D. T=2
π

8. T×m chu kú cđa hµm sè y=tan2x
A. T=
π
/2 B. T=4
π

C. T=2
π
D. T=
π
9. Trong c¸c hµm sè sau hµm sè nµo
tn hoµn?
A. y=x+cos2x B. y=xcos2x
C. y=cos2x D. y=x
2
+3
10. Trong c¸c hµm sè sau hµm sè nµo
tn hoµn?
A. y=2x-x
3
B. y=cosx
C. y=xcosx D. y=sinx-x
-Chọn đáp án trắc nghiệm :
1A, 2A, 3B, 4D, 5D, 6B, 7A, 8A,
9C,10B.

-Tương tự cho hai hàm số y=cosx và y=
cotx.
-Tổng quat cho hàm số: y= sin(ax+b) và
y=cos(ax+b), y= tan(ax+b) và y=cot(ax+b)?
- Chu kỳ tương ứng của các hàm số trên
theo công thức T/a?
-Công thức tìm chu kỳ của của số cho bởi
tổng các hàm số?
Hoạt động 6. Trắc nghiệm kiến thức.
Câu 1. 1. T×m chu kú cđa hµm sè y = cosx/3
A. T=6
π
B. T=2
π

C. T=k2
π
D. T=3
π

2. Trong c¸c hµm sè sau hµm sè nµo tn
hoµn?
A. y=cotx B. y=x+tanx
C.
x
x
y
sin
=
D. y=x

2
+3
3. Trong c¸c hµm sè sau hµm sè nµo tn
hoµn?
A. y=x+1 B. y=sinx
C. y=xsinx D. y=x
2

4. T×m chu kú cđa hµm sè y=cosx
A. T=2
π
/3 B. T=k2
π

C. T=
π
D. T=2
π

5. T×m chu kú cđa hµm sè y= tanx
A. T=2
π
B. T=
π
/2
C. T=k
π
D. T=
π
@ Cđng cè dỈn dß.

- §N các hàm số lượng giác, tính chẵn, lẻ của các hàm số lượng giác, tính tuần
hoàn của các hàm số lượng giác.
- Phương pháp tìm tập xác đònh của hàm số, xét tính chẵn, lẻ của hàm số
- Phương pháp xét tính tuần hoàn và tìm chu kỳ của hàm số.
- Về nhà xem phần sự biến thiên và đồ thò hàm số LG.
@ Rót kinh nghiƯm bỉ sung.
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
........................................................................................................................................