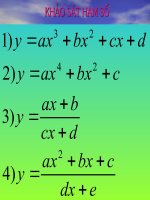Slide tóan 12 KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ _Thị Mơ
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.53 MB, 30 trang )
UBND TỈNH ĐIỆN BIÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO
Cuộc thi Thiết kế bài giảng điện tử e – Learning
Bài giảng:
Tiết 19: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Chương trình Giải tích, lớp 12 - GDTX
Giáo viên : Nguyễn Thị Mơ
Email :
Điện thoại : 0912824240
Đơn vị : Trung tâm GDTX tỉnh
Tháng 1/2015
Chương I:
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ
Bài 5 – Tiết 19
Khảo sát sự biến thiên và vẽ đồ thị của hàm
số
III. Sự tương giao của các đồ thị
Mục tiêu bài học
* Kiến thức
!
"#$%
* Kỹ năng
&'()*+",#- !"%
.Thái độ
/0 ,12(+3
41$,!5(678%
Gợi ý trả lời
,9:2;<=2
>
3?
>
@A!?BC=2@(DA
$EF"G9
H/G94"I4?BC=2@??B?
>
,2B2
>
6?
>
BC=2
>
@
<!,J<(D!
9K #LM N OPM
#9 Q6R+A#$ST+E(
H/F9U<"V"LP!W2?M
?BC=2@"V-"L?
Kiểm tra bài cũ
/9?BC=2@B2
G
HG2XA=/
F
@
?B=2@B2FA=/
G
@
@U;2EY=F3>@,Z=G3[@,/=X3\@A!=/
F
@(D]
@U;2EY=F3>@,^=G3F@,_=\3[@A!=/
G
@(D]
@KM"V-!"LP!%
#@UP!"V%
1. Tìm tọa độ giao điểm của hai đồ thị
III. Sự tương giao của các đồ thị
1. Tìm tọa độ giao điểm của hai đồ thị
<R`hoành độ giao điểm
nghiệmI492
G
HG2XB2F]
Cau 3
III. Sự tương giao của các đồ thị
1. Tìm tọa độ giao điểm của hai đồ thị
4A9V!2BF,2BG1
I492
G
HG2XB2aF
=?C=2@B=2@@
<R`hoành độ giao điểm
nghiệmI492
G
HG2XB2F]
Itìm tọa độ giao điểm ?BC=2@?B=2@]
b6G?BC=2@?B=2@A
<=2
>
3?
>
@C=2
>
@B=2
>
@B?
>
V2
>
I49C=2@B=2@
III. Sự tương giao của các đồ thị
1. Tìm tọa độ giao điểm của hai đồ thị
4P!?BC=2@,?B=2@
Phương pháp
+ B3.Q6 c
+ B1. d+I49C=2@B=2@!,+eA
2B2
F
,2B2
G
+ B2. 4!6?
F
,?
G
f?2B2
F
,2B2
G
"?BC=2@=T?B=2@@
Kiểm tra bài cũ
/?BC=2@B2
G
HG2XA=/
F
@?B=2@B2FA=/
G
@
#@UP!"V
Giải
!I49
K ?AY=F3>@<=G3X@
y = 0
y = -3
Ví dụ
4P!?B2
X
X2
G
H[?B[
Cau 1
Ví dụ
4P!?B2
X
X2
G
H[?B[
Giải
!I49
K ?AY=>3[@Z=X3[@
bVR`số nghiệm "2
X
X2
G
H[B[
số giao điểm ]
y = 5
y = 5
số nghiệm = số giao điểm
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
Chú ý:
g?BC=2@?B=2@
bằngI49C=2@B=2@
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
j[9AFI4AF
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
j[9AFI4AF
B[9AGI4AGk
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
j[9AFI4AF
B[9AGI4AGk
Fll[9AXI4AXk
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
j[9AFI4AF
B[9AGI4AGk
Fll[9AXI4AXk
BF9AGI4AGk
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Giải:
gI492
X
X2
G
H[Bf?B2
X
X2
G
H[hi?B
^$A9
j[9AFI4AF
B[9AGI4AGk
Fll[9AXI4AXk
BF9AGI4AGk
lF9AFI4AF
j[TlF9AFI4AF
B[TBF9AGI4AGk
Fll[9AXI4AXk
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 2
/?B2
\
G2
G
XA=/@M%^$
=/@,"I49x
4
- 2x
2
= m + 3 A\$k%
Cau 2
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 2
/?B2
\
G2
G
XA=/@M%^$
=/@,"I49x
4
- 2x
2
= m + 3 A\$k%
Giải:
4A92
\
G2
G
BHX2
\
G2
G
XB
gI492
\
G2
G
XBf?B2
\
G2
G
Xhi?B
^$A9
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 2
/?B2
\
G2
G
XA=/@M%^$
=/@,"I49x
4
- 2x
2
= m + 3 A\$k%
Giải:
4A92
\
G2
G
BHX2
\
G2
G
XB
gI492
\
G2
G
XBf?B2
\
G2
G
Xhi?B
^$A9
\llX9A\kI4A\k%
2. Biện luận số nghiệm phương trình dựa vào đồ thị
Ví dụ 2
/?B2
\
G2
G
XA=/@M%^$
=/@,"I49x
4
- 2x
2
= m + 3 A\$k%
Ví dụ 1
^$
?B2
X
X2
G
H[=M@, E
$I49
x
3
- 3x
2
+ 5 = m
Cách giải dạng toán:
Biện luận số nghiệm phương trình dựa vào đồ thị hàm số y = f(x)
/6+#J9Z E$!"#$
?BC=2@]
B1%:"Oc#JC=2@BZ4=@=.@
B2.m 9g"=.@f?BC=2@?BZ4=@
B3.KMhA"V-!"LP!V"hc
Ví dụ 3
/7"f=/@D5hi=#@9?B2HJk8P"
%
Giải:
=/@D5=#@Jk6"Ak8P
4A9
U;"=.@,AnB
G
HFGj>8P"
2BG(Do=.@V"DA(G
K ?=/@=#@D5Jk%
2. Biện luận số nghiệm phương trình dựa vào đồ thị