DIỆN TÍCH HÌNH PHẲNG

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

094.673.6868

Lêi Giíi ThiƯu

Mục lục
MỘT SỐ PHƯƠNG PHÁP GIẢI
MỘT LỚP CÁC BÀI TOÁN DIỆN TÍCH HÌNH PHẲNG

Lời giới thiệu
Phần thứ nhất: Kiến thức cơ bản
Phần thứ hai: Các bài tốn về diện tích hình phẳng
Phần thứ ba: Bài tập minh họa phương pháp
Phần thứ tư: Bài tập tự luyện

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

Trang
1
2
6
14
54

Chúc các em học sinh ôn tập thật tốt
và dành kết quả thật cao trong hai kỳ thi tới!

Trong chương trình tốn 12 mà cụ thể là phân mơn Giải tích

các em học sinh được tiếp cận với bài tốn diện tích hình phẳng trong
Chương III. Trong bài học đó Sách giáo khoa đề cập đến một số bài
tốn cơ bản của diện tích hình phẳng.
Xong để giải quyết bài tốn này mà chỉ biết áp dụng cơng
thức thơi thì chưa đủ, bởi với bài tốn tính diện tích của một hình
phẳng các em sẽ gặp ở đó những tích phân của các hàm có chứa dấu
giá trị tuyệt đối, mà việc tính tích phân này khơng phải dễ dàng gì đối
với tất cả các em học sinh.
Hơn nữa, thực tế trong những năm gần đây kể từ khi Bộ giáo
dục cải tiến phương thức ra đề theo hình thức 3 chung thì câu hỏi về
phần tích phân nói chung hay ứng dụng của tích phân nói riêng có
xác suất xuất hiện thường xuyên hơn trong các đề thi Tốt nghiệp
THPT và thi vào các trường Đại học.
Với tất cả những lý do trên, cùng với những kinh nghiệm của
bản thân đã trực tiếp giảng dạy học sinh lớp 12 và luyện thi Đại học.
Tôi mạnh dạn tổng hợp, phân loại và viết bài giảng “MỘT SỐ
PHƯƠNG PHÁP GIẢI MỘT LỚP CÁC BÀI TỐN DIỆN
TÍCH HÌNH PHẲNG” để trao đổi với các bạn đồng nghiệp và làm
tài liệu giúp các em học sinh ôn luyện trong kỳ thi tốt nghiệp THPT
và thi vào các trường Đại học.
Trong bài giảng này tôi đã đề xuất 4 phương pháp để giải
quyết bài tốn diện tích hình phẳng, đó là: phương pháp xét dấu,
phương pháp đưa dấu giá trị tuyệt đối ra ngồi dấu tích phân,
phương pháp đồ thị và phương pháp giả định và gần 20 bài tập để
minh họa cho cả 4 phương pháp. Sau mỗi lời giải của mỗi bài tốn
tác giả đều có những nhận xét giúp bạn đọc có thể chọn ra cho mình
những phương pháp giải tối ưu nhất, để có được những lời giải gọn
gàng và sáng sủa nhất./.
Thạch Thất, ngày 20 tháng 02 năm 2011
Tác giả

Nguyễn Văn Dũng

Trang 56

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 1


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Phần thứ nhất

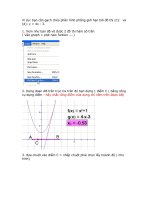
21. y = tanx, y = 0, x= 0, x =

KIẾN THỨC CƠ BẢN

S   f ( x)dx  F ( x)
a

b
a

 F (b)  F (a )

(Trong đó F(x) là một nguyên hàm của hàm số f(x) trên đoạn

tập K, với a, b  K)
2. Các tính chất của tích phân.
a

2.1).

 f ( x)dx  0
a
b

2.2).


b

2.3).

b
c

c

b
b

a

a

b

2.6).

b

- Hết -

a

b

2.5).  k . f ( x)dx k  f ( x)dx
a

x2
chia hình trịn có tâm tại gốc tọa độ, bán
2

kính R = 2 2 thành hai phần. Tính tỷ số diện tích của chúng.

  f ( x)  g ( x)dx  f ( x)dx   g ( x)dx
b

8
3

a

b

2.4).


4

Bài 2:
Cho Parabol (P): y = x2 + 1 và đường thẳng d: y = mx + 2.
1). Tìm m để hình phẳng giới hạn bởi (P) và (d) có diện tích nhỏ
nhất.
2). Gọi A(-1;1), B(2; 4) là hai điểm trên (P), tìm điểm M trên
cung AB để diện tích tam giác ABM lớn nhất.
Bài 3: Parabol y 

 f ( x)dx   f ( x)dx   f ( x)dx
a

(P) tại M và trục Oy là

a

f ( x)dx    f ( x )dx

a

094.673.6868

22. y = x2 – 2x + 2, y = x2 + 4x + 5, y = 1
23. Tìm hồnh độ của điểm M trên parabol (P) y = x2 + 2 sao
cho diện tích hình phẳng giới hạn bởi (P), tiếp tuyến của

1. Cơng thức Niutơn – Laibơnit.
b

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

(k  R )

a
b

b

  f ( x)  g ( x)dx   f ( x)dx   g ( x)dx
a

a

a
b

2.7). Nếu f(x)  0 trên đoạn [a; b] thì

 f ( x)dx  0
a
b

2.8). Nếu f(x)  0 trên đoạn [a; b] thì  f ( x)dx  0
a

Trang 2

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 55


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Phần thứ tư
BÀI TẬP TỰ LUYỆN
Bài 1: Tính diện tích hình phẳng giới hạn bởi các đường sau.

1. y = cos2x, y = 0, x = 0, x 
4

2. y = x3 + 3x2, trục hoành, x = - 2, x = -1
2x  1
, trục hoành, trục tung.
x 1
 3x  1
4. y 
, trục hoành, trục tung.
x 1

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

3. Một số phương pháp tính tích phân.
Ngoài phương pháp sử dụng bảng nguyên hàm cơ bản để tính
tích phân ta cịn dụng đến phương pháp đổi biến số và phương
pháp tích phân từng phần.
3.1. Phương pháp đổi biến số.
Cho hàm số y = f(x) liên tục trên đoạn [a; b], giả sử hàm x =
u(t) có đạo hàm liên tục trên đoạn [  ;  ] sao cho u(  ) = a,

3. y 

5. y = x2 – 3x + 2, y = x + 1, x = 0
6. y   4  x 2 , x2 + 3y = 0
7. y = x2 + 1(P), trục Oy và tiếp tuyến của (P) tại điểm

M(2; 5)
8. y  2 1  x 2 , y = 2(1 – x)
9. y = x2, y  x
10. y = - x2 + 4x , y= x
11. y = ex, y = 2, x = 1
12. y = x2 – 4x + 5 và các tiếp tuyến của nó tại A(1; 2) và
B(4; 5)
13. y = 2x2 , y = x4 – 2x2, x  0
x2
14. y = x, y = 1, y  , x  0, y  1
4

15.
16.
17.
18.

19.
20.

y = x2 , y = 4x – 4, y = - 4x – 4
y = |lnx|, y = 1
y = sin|x|, y = |x| - 
y2 – 2x = 0 , x + y = 0
y2 = 2x, x - 2y + 2 = 0, y = 0, trục Ox
y2 = 2x, 27y2 = 8(x – 1)3

094.673.6868



b

u(  ) = b và a  u(t)  b, ta có:



f ( x)dx   f u (t ).u ' (t )dt .

a



Chú ý: Một số dấu hiệu dùng phép đổi biến
- Hàm lũy thừa u  (x)  đặt t = u(x)
- Hàm mũ au(x)

 đặt t = u(x)

- Hàm phân thức

 đặt t = mẫu số

- Hàm chứa căn

 đặt t = căn

- Hàm chứa

a 2  x2

 đặt x = a.sint (a > 0, t  [-  /2;  /2]

- Hàm chứa

x2  a 2

 đặt x = a/sint (a > 0, t  [0;  /2]

- Hàm chứa

x2  a 2

 đặt x = a.tant (a > 0, t  (-  /2;  /2)

3.2. Phương pháp từng phần.
Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên

b

b b
[a;b] thì:  u ( x ).v ' ( x).dx  u ( x).v( x)   v( x ).u ' ( x ).dx
a a
a
b

b b
hay  u.dv  u.v   v..du
a a
a

Chú ý: Một số dấu hiệu dùng phép từng phần

Trang 54

Bài toán diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 3


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

 Đặt u = P(x)

 P( x). sin f ( x)dx
hoặc  P( x ). cos f ( x)dx
 P( x).e dx

 P( x). ln f ( x)dx

 Đặt u = P(x)

 Đặt u = ln f(x)

f ( x)

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Nhận xét sau lời giải:
- Đây là một bài tập tương đối khó vì 2 lí do: thứ nhất đây
là bài tốn tính diện tích hình phẳng nhưng giả thiết của
bài toán chưa được cụ thể, thứ hai đây lại là bài toán cực
trị.

4. Giá trị tuyệt đối và tích phân chứa giá trị tuyệt đối.
4.1. Giá trị tuyệt đối.
 f ( x ) khi f ( x)  0
f ( x)  
 f ( x) khi f ( x )  0

Hệ quả: (ý nghĩa hình học):
a). Xét đồ thị (C) của hàm số y = f(x) liên tục trên [a; b]

- Nếu (C) nằm trên trục hồnh thì f(x)  0 với mọi x  [a; b],
khi đó, ta có: |f(x)| = f(x),  x  [a; b].
- Nếu (C) nằm trên dưới hồnh thì f(x)  0 với mọi x  [a; b],
khi đó, ta có: |f(x)| = - f(x),  x  [a; b].
b). Xét đồ thị (C) của hàm số y = f(x) và đồ thị (D) của hàm số
y = g(x) liên tục trên đoạn [a; b].
- Nếu (C) nằm trên (D) trên đoạn [a;b] thì f(x)  g(x) trên [a; b]
Khi đó, ta có: |f(x) – g(x)| = f(x) – g(x) ,  x  [a; b].
- Nếu (C) nằm dưới (D) trên [a;b] thì f(x)  g(x) trên [a; b]
Khi đó, ta có: |f(x) – g(x)| = g(x) – f(x),  x  [a; b].
4.2. Tích phân chứa giá trị tuyệt đối.
b

Xét tích phân I   f ( x) dx
a
b

a). Nếu f(x)  0  x  [a; b] thì I =

 f ( x)dx

 0

a
b

b). Nếu f(x)  0  x  [a; b] thì I = -

 f ( x)dx

 0

a

c). Nếu f(x) đổi dấu trên đoạn [a; b],

Trang 4

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 53


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Mặt khác ta có:

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

chẳng hạn f(x)  0  x  [a; c] và f(x)  0  x  [c; b]

2

2

2 2

2

c

b

c

b

AB  (b  a )  (b  a )  (b  a) 1  (b  a )  b  a

thì ta có: I   f ( x ) dx   f ( x ) dx   f ( x)dx   f ( x )dx

Theo giả thiết AB = 2  0  b – a  2 (2)

d). Nếu f(x) giữ nguyên dấu trên [a; b] ta có:

a

4
3
b  a  0
a  1
4
Vậy MaxS =
 


3
 b 1
b  a  2
 A(- 1; 1) và B( 1; 1)

c

b

Từ (1) và (2)  S 

a

c

b

I   f ( x) dx = |  f ( x)dx |
a

a

(Đưa dấu giá trị tuyệt đối ra ngồi dấu tích phân)

Câu 2: Gọi A(a; a2) , B(b; b2) ( với giả thiết a < b)
 phương trình đường thẳng qua 2 điểm A, B là: y = (b + a)x –
ab, (d)
Mặt khác ta có: (d) đia qua I(1; 3) nên ta có: 3 = a + b – ab  a
+ b = 3 + ab (*)

Gọi S là diện tích hình phẳng cần tìm, ta có:
b

S 
a

b

 (b  a ) x 2
x3 

 abx  
(b  a) x  ab  x dx  
2
3 a




2



 ( a  b) 2
b 2  ab  a 2 
 (b  a ) 
 ab 

3
 2





3

b  a
S
(đvdt) (3)

2

6

Từ (*), ta suy ra:
(a + b) = ( 3 + ab)2
2
2
2
 (b – a) = 8 + (ab + 1)  (b – a)  8 hay b – a  2 2 (4)
 Từ (3) và (4)  S 

Vậy MinS =

8 2
3

8 2
3
 ab  1  0

a  b  3  ab

Đạt được  

 ab  1
 
 (d) : y = 2x +1
a  b  2

Trang 52

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 5


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Phần thứ hai
CÁC BÀI TỐN VỀ TÍNH DIỆN TÍCH HÌNH PHẲNG
1. Một số bài tốn cơ bản.
Bài tốn 1: Hình phẳng giới hạn bởi một đường cong và trục
hồnh.
Xét hình phẳng D giới hạn bởi các đường y = f(x), y = 0,
x = a, x = b.
b

Ta có: S   f ( x) dx
a

Chú ý:
- Trong thực tế giả thiết của bài tốn 1 có thể khơng cho
trước cận lấy tích phân (tức là không cho x = a, x = b).
- Cho dù giả thiết cho hay không cho cận lấy tích phân, thì
việc đầu tiên ta phải làm là tìm nghiệm của PT f(x) = 0.
- Sau đó cần lập cơng thức tính diện tích của D và sử dụng
1 trong 4 phương pháp sẽ đề cập sau đây để tính diện tích.

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

thẳng qua 2 điểm A, B đạt giá trị lớn nhất.
2). Gọi d là đường thẳng đi qua I(1; 3), tìm phương trình
đường thẳng d sao cho diện tích hình phẳng giới hạn bởi (P)
và d đạt giá trị nhỏ nhất.
Nhận xét trước khi giải.
- Đây là một bài toán cực trị về diện tích hình phẳng, nên
trước hết ta cần lập cơng thức tính diện tích S(tức là thiết
lập các giả thiết liên quan đến S)
- Với câu 1, trước hết ta cần giả thiết về tọa độ A, B  lập
phương trình đường thẳng qua 2 điểm A, B  diện tích
S.
- Với câu 2, thực chất cũng là việc xác định 2 điểm A, B
trên (P) với điều kiện I  AB , khác với câu 1 là xác định
A, B với điều kiện AB = 2.

- Sau khi đã tính được S, ta cần sử dụng phương pháp thích
hợp để tìm giá trị lớn nhất, nhỏ nhất của S.
Câu 1: Gọi A(a; a2) , B(b; b2) ( với giả thiết a < b)
 phương trình đường thẳng qua 2 điểm A, B là: y = (b + a)x –
ab, (d)

Bài tốn 2: Hình phẳng giới hạn bởi hai đường cong.

Gọi S là diện tích hình phẳng cần tìm, ta có:
b

S 
a

Trang 6

Bài tốn diện tích hình phẳng

b

 (b  a ) x 2
b  a 3 (1)
x3 
 abx   
(b  a) x  ab  x dx  
2
3 a
6




2



Bài tốn diện tích hình phẳng.

Trang 51


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

4x = (4 – x)3  (x – 2)(x2 – 10x + 32) = 0  x = 2

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Xét hình phẳng D được giới hạn bởi các đường y = f(x),
y = g(x), x = a, x = b.
b

Ta có: S   f ( x)  g ( x) dx
a

Chú ý:
- Nếu trong giả thiết của bài tốn 2 ta thay g(x) = 0 thì ta sẽ

có bài tốn 1.
- Trong thực tế giả thiết của bài tốn 2 có thể khơng cho
trước cận lấy tích phân (tức là khơng cho x = a, x = b).
- Cho dù giả thiết có cho hay khơng cho cận lấy tích phân,
thì việc đầu tiên ta phải làm là tìm nghiệm của phương
trình f(x) – g(x) = 0.
- Sau đó cần cần lập cơng thức tính diện tích của D và sử
dụng 1 trong 4 phương pháp đề cập sau đây để tính diện
tích S.

Với x = 2  y2 = 8  y  2 2
Gọi S là diện tích hình phẳng cần tìm, từ hình vẽ ta có:
S = S1+S2 = 2S1
2 2

2 2

 3 2 y2 
 33 5 y3 
 2  4 y  dy 24y  y    152 2
4
12 0
15
 5
0 
Nhận xét sau lời giải 3:
- Từ hình vẽ ta thấy rằng phần hình phẳng cần tính diện
tích có trục đối xứng là trục hồnh nên ta có thể viết S =
S1 + S2, trong đó S1 là diện tích của hình phẳng được giới
hạn bởi các đường x 

-

y2
, x  4  3 y 2 , y = 0, y  2 2 .
4

Từ hình vẽ ta thấy rằng đồ thị của (d): x  4  3 y 2 nằm
trên

đồ
2 2

S1 


0

thị

của

y2
(P): x 
4

nên

ta

có:


y2 
 4  3 y 2  dy
4 


Bài 16: Cho (P) y = x2
1). Gọi A, B là 2 điểm trên (P) sao cho AB = 2, tìm tọa độ A,
B sao cho diện tích hình phẳng giới hạn bởi (P) và đường

Trang 50

Bài tốn diện tích hình phẳng

Bài tốn 3: Hình phẳng giới hạn bởi các đường cong tự cắt
khép kín.
Với bài tốn này giả thiết có thể cho hình phẳng giới hạn bởi
2 , 3 hay 4 đường cong hoặc nhiều hơn. Khi đó để giải quyết
bài toán này ta sẽ sử dụng phương pháp đồ thị để tìm lời giải,
ta cần làm theo trật tự sau đây:
- Bước 1: Vẽ đồ thị của tất cả các đường đã cho trên cùng 1
hệ trục tọa độ.
- Bước 2: Xác định phần hình phẳng cần tính diện tích.
- Bước 3: Tìm hồnh độ giao điểm của các đường cong
- Bước 4: Chia nhỏ phần hình phẳng cần tính diện tích bởi
các đường thẳng x = c ( x = c chính là hồnh độ giao điểm
của các đường cong tìm được ở bước 3).
- Bước 5: Lập cơng thức và tính diện tích S.
2. Chú ý.

Tương tự (bằng cách coi x là hàm, y là biến) thì diện tích
hình phẳng giới hạn bởi các đường x = f(y), x = g(y) và hai
đường thẳng y = c, y = d là:

Bài tốn diện tích hình phẳng.

Trang 7


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

d

S   f ( y )  g ( y ) dy
c

(trong đó x = f(y), x = g(y) là hai hàm liên tục trên đoạn [c; d])
3. Một số phương pháp tính diện tích của hình phẳng.
Bạn đọc thân mến, bản chất của việc tìm diện tích của
một hình phẳng là tính các tích phân có dấu giá trị tuyệt đối,
trong phần này sẽ giới thiệu 4 phương pháp tính tích phân chứa
dấu gái trị tuyệt đối đây cũng là 4 phương pháp tính diện tích
hình phẳng.

Từ y 2  4 x  x 

y  2 2

Gọi S là diện tích hình phẳng cần tìm, ta có:
2 2

S



2 2



2

Xét tích phân S   f ( x) dx

0

a

Thì ta có: S =



b

 f ( x)dx   f ( x)dx   f ( x)dx
a

Chú ý:
- Để có thể lập được bảng xét dấu của biểu thức f(x) như trên,
trước tiên ta cần tìm nghiệm của phương trình f(x) = 0 thuộc
đoạn [a; b].
- Xét dấu trực tiếp biểu thức f(x) là việc ta sử dụng bảng xét dấu
như trên (bảng này xét dấu dựa trên các định lý về dấu của các
đa thức ẩn x).

y2
4  y  dy  2
4
3

2 2

b



y2
(P) và y 2  4  x 3  x  4  3 y 2 (d)
4

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:
4x = (4 – x)3  (x – 2)(x2 – 10x + 32) = 0  x = 2
Với x = 2  y2 = 8  y  2 2
 (P) và (d) cắt nhau tại 2 điểm có tung độ là y  2 2 và

Phương pháp 1: Xét dấu biểu thức trong dấu giá trị tuyệt
đối.

Để xét dấu của biểu thức f(x) trên đoạn [a; b] ta có thể sử
xét dấu trực tiếp hoặc gián tiếp bằng cách giải các BPT tương
ứng. Sau đó tách tích phân I thành tổng của các tích phân trên
các đoạn con, mà trên mỗi đoạn con này f(x) không đổi dấu.
Chẳng hạn ta có bảng xét dấu của f(x) trên đoạn [a; b] như sau.
x
a


b
f(x)
+
+

094.673.6868

2 2

2


0

y2
4  y  dy
4
3

2

2 2



y2 
3
y3 
 4  3 y 2  dy  2  4 y  3 y 5  
4 
5
12  0



 28 2 

12 2 4 2 152 2


(đvdt)
5
3
15

Lời giải 2: (phương pháp giả định)
2 2

S


2 2
2 2

2


0

y2
4  y  dy  2
4
3

2

2 2


0

y2
4  y  dy
4
3

2

2 2



y2 
3
y3 
 4  3 y 2  dy  2 4 y  3 y 5  
4 
5
12  0





152 2
15

Nhận xét sau lời giải 2:
Sau khi giả định kết quả ta thu được S =

152 2
> 0, nên điều
15

giả định trên là đúng.
Lời giải 3: (phương pháp đồ thị)
y2
Từ y  4 x  x 
(P) và y 2  4  x 3  x  4  3 y 2 (d)
4

2

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:

Trang 8

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 49


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Từ hình vẽ, nếu ta gọi S là diện tích cần tìm thì S = S1 + S2 ,
trong đó S1 là diện tích của phần hình phẳng giới hạn bởi các
đường y  5  x , y = 3 – x, x =1, x = 4; và S2 là diện tích của
phần hình phẳng giới hạn bởi các đường y  5  x ,
y   5  x , x = 4, x = 5.
4





Ta có S1   5  x  (3  x) dx 
1

5



19
(đvdt)
6

4
(đvdt)
3
19 4 9
Vậy S = S1 + S2 =
  (đvdt)
6 3 2



S2   5  x  ( 5  x ) dx =
4

Nhận xét sau lời giải 5:
- Bằng việc coi x là biến, y là hàm ta cũng đã giải quyết
xong bài toán bằng phương pháp đồ thị, xong vẫn cịn hơi
dài và chưa sáng sủa.
- Tóm lại khi gặp các bài toán dạng này ta nên sử dụng
phương pháp đồ thị.
Bài 15: Tính diện tích của hình phẳng giới hạn bởi các
đường y 2  4 x , y 2  4  x 3
Nhận xét trước khi giải.

- Giả thiết của bài toán này cho cả hai hàm số y 2  4 x ,
3
y 2  4  x  (có bậc hai đối với y, còn bậc của x là lẻ) nên
ta sẽ coi x là hàm và y là biến. Tức là từ giả thiết ta phải
rút x theo y.
- Việc coi x là hàm và y là biến không hề ảnh hưởng đến
kết quả bài tốn diện tích hình phẳng.
- Ta sẽ giải bài toán này theo phương pháp đưa dấu giá trị
tuyệt đối ra ngoài và giả định.
Lời giải 1: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)

Trang 48

Bài tốn diện tích hình phẳng

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

- Xét dấu gián tiếp được thực hiện khi việc xét dấu trực tiếp
khơng thực hiện được (ví dụ với biểu thức f(x) = ex – e- x + 2 ta
khơng thể dùng bảng để xét dấu). Khi đó ta đi giải Bất phương
trình f(x) > 0 (hoặc f(x) < 0).
Phương pháp 2: Dùng đồ thị của hàm số.
Trong phương pháp này ta cần ghi nhớ các kết quả sau
Kết quả 1: Nếu trên
y
đoạn [a; b] đồ thị
y = f(x)
của hàm số y = f(x)

liên tục và nằm trên
trục hồnh thì ta có:

a

O

b

x

b

S   f ( x) dx
a
b

=

 f ( x)dx
a

Kết quả 2: Nếu trên
đoạn [a; b] đồ thị
của hàm số y = f(x)
liên tục và nằm dưới
trục hồnh thì ta có:

y
a

b

x

O

b

S   f ( x) dx

y = f(x)

a
b

= -

 f ( x)dx
a

Bài tốn diện tích hình phẳng.

Trang 9


Nguyễn Văn Dũng – THPT Hai Bà Trưng.
Kết quả 3: Nếu trên
đoạn [a; b] đồ thị
của hàm số y = f(x)

liên tục và nằm trên
đồ thị hàm số y =
g(x) thì ta có:

y

094.673.6868

2

y = f(x)



O

x

1

  f ( x)  g ( x) dx
a

Kết quả 4: Nếu trên
đoạn [a; b] đồ thị
của hàm số y = f(x)
liên tục và nằm dưới
đồ thị hàm số y =
g(x) thì ta có:

y

y = g(x)
b

a
O

x
y = f(x)

b

 g ( x)  f ( x) dx
a

Để thực hiện được theo phương pháp này, ta cần tiến hành
theo các bước sau:
 Bước 1: Vẽ đồ thị của các hàm số trong giả thiết trên cùng hệ
trục tọa độ.
 Bước 2: Xác định phần hình phẳng cần tính diện tích.
 Bước 3: Tìm hồnh độ giao điểm của các đường cong tự cắt.
 Bước 4: Chia nhỏ phần hình phẳng cần tính diện tích bởi các
đường thẳng x = c (x = c chính là hồnh độ giao điểm
của các đường cong tìm được ở bước 3).
 Bước 5: Lập cơng thức và tính diện tích S.

Trang 10

1

2

 y3 y 2

9
   y 2  y  2 dy      2 y   (đvdt)
2
1
 3
 1 2

b

a

2

2

a

b



S   f ( y)  g( y) dy    y 2  y  2 dy

b

S   f ( x)  g ( x) dx =

2

2

Lời giải 4: (phương pháp giả định)
2

y = g(x)

094.673.6868

 y3 y 2

9
 y  y  2 dy   

 2 y  
2
 3
 1 2



1

b

a

S   f ( x)  g ( x) dx

=

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

Bài tốn diện tích hình phẳng

( Kết quả S > 0, chứng tỏ điều giả định trên là đúng)
Nhận xét sau khi giải.
- Đây là một bài toán đặc biệt mà ta coi y là biến, x là hằng
 lời giải sẽ gọn gàng và sáng sủa.
- Một lời khuyên nhỏ là khi gặp các hàm số mà bậc của y
khác 1 thì ta nên coi y là biến và x là hàm.
- Tất nhiên bài này ta vẫn có thể coi x là biến, y là hàm
được, nhưng lời giải có thể khơng đẹp bằng các cách
trên.
Lời giải 5: (coi x là biến, y là hàm)
Nhận xét trước khi giải.
- Trước hết lưu ý rằng: y2 + x – 5 = 0  y   5  x 
giả thiết cho 3 đường y  sử dụng phương pháp đồ thị.
- Hoành độ giao điểm của 2 ĐTHS y = 3 – x và y  5  x là
nghiệm của phương trình: 3 – x  5  x  x = 1.
- Hoành độ giao điểm của 2 ĐTHS y  5  x và y   5  x là
nghiệm của phương trình: 5  x   5  x  x = 5.
- Hoành độ giao điểm của 2 ĐTHS y = 3 – x và y   5  x là
nghiệm của phương trình: 3 – x   5  x  x = 4.

Bài tốn diện tích hình phẳng.

Trang 47


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

5 – y2 = 3 – y  y = - 1 hoặc y = 2
Đặt f(y) = 5 - y2 và g(y) = 3 – y,
ta có: f(y) – g(y) = - y2 + y + 2.
Ta có bảng xét dấu của f(y) – g(y) là
y

-1

f(y) – g(y)

+

-

b

S

2



f ( y )  g ( y ) dy  

1

1

a

2

 y3 y2

9
 y 2  y  2 dy   

 2 y  
2
 3
 1 2



b

S   f ( x) dx = |  f ( x)dx |”

Diện tích của hình phẳng cần tìm là:
2

094.673.6868

Phương pháp 3: Đưa dấu giá trị tuyệt đối ra ngồi dấu tích
phân.
Đơi khi việc xét dấu của biểu thức f(x) trên [a; b] thực sự
khơng đơn giản, bởi trên mặt bằng lí thuyết các em chỉ được
học cách xét dấu của các đa thức ẩn x mà thơi, khi đó ta sử dụng
kết quả sau:
“Nếu f(x) giữa nguyên dấu trên [a; b] ta có:

2

-

Nguyễn Văn Dũng – THPT Hai Bà Trưng.



a

Để thực hiện được theo phương pháp này, ta tiến hành theo
các bước sau:
 Bước 1: Tìm các nghiệm thuộc đoạn [a; b] của PT f(x) = 0.

Lời giải 2: (phương pháp đồ thị)

b

 Bước 2: Tách tích phân S   f ( x) dx thành tổng của các tích
a

phân trên các đoạn con, chẳng hạn:





b

b

S   f ( x) dx =  | f ( x) | dx   | f ( x ) | dx   | f ( x) | dx


a

a



(trong đó  ,  là các nghiệm thuộc đoạn [a; b] của PT f(x) =
0)
 Bước 3: Đưa dấu giá trị tuyệt đối dưới dấu tích phân ra bên
ngồi dấu tích phân, chẳng hạn:




Từ hình vẽ trên, nếu gọi S là diện tích cần tìm, ta có:
2

S

 5  y  3  y dy
2

1

2





   y 2  y  2 dy 
1

9
(đvdt)
2

Lời giải 3: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)
2

S



1

Trang 46

2

f ( y )  g ( y ) dy 

y

2

 y  2 dy

1

Bài tốn diện tích hình phẳng

S=


a

f ( x )dx 



b

f ( x )dx 



 f ( x)dx

 Bước 4: Tính tốn và ra kết quả.
Phương pháp 4: Phương pháp giả định.
Trong phương pháp 3 ta đã đề cập đến việc đưa giá trị
tuyệt đối ra ngồi dấu tích phân, điều này có thể hơi “cồng
kềnh” vì khi tích phân ta tính ln có dấu trị tuyệt đối bên ngoài
kèm theo. Để khắc phục nhược điểm này ta có thể sử dụng
phương pháp giả định sau đây.

Bài tốn diện tích hình phẳng.

Trang 11


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

b

Giả sử ta phải tính tích phân S   f ( x) dx ( với điều kiện biểu
a

thức f(x) không đổi dấu trên [a; b]), khi đó ta có thể giả sử:
b

S=

 f ( x)dx

-

b

 Vậy S = -

 f ( x)dx

=-m

a

Để thực hiện được theo phương pháp này, ta tiến hành theo
các bước sau:
- Bước 1: Tìm các nghiệm thuộc đoạn [a; b] của PT f(x) = 0.
b

- Bước 2: Tách tích phân S   f ( x) dx thành tổng của các tích
a

phân trên các đoạn con, chẳng hạn:




b

b

S   f ( x) dx =  | f ( x) | dx   | f ( x ) | dx   | f ( x) | dx


a

a



(trong đó  ,  là các nghiệm thuộc đoạn [a; b] của PT f(x) = 0
và hiển nhiên rằng trên các đoạn con [a;  ], [  ;  ], [  ; b]
biểu thức f(x) không đổi dấu, tức là f(x) luôn không âm, hoặc
không dương )
- Bước 3: Bỏ dấu || trong tất cả các tích phân và thay vào đó là
các dấu cộng (+) và trừ (-) xen kẽ nhau ( nếu  ,  là các
nghiệm đơn hoặc nghiệm bội lẻ). Trong trường hợp nếu cận nào
đó là nghiệm bội chẵn thì 2 tích phân chung cận đó có cùng một
dấu, chẳng hạn:


S=


a

Trang 12



b

f ( x)dx   f ( x )dx   f ( x)dx (1)



Ta có :
1



1



2

S 3   x  5  ( x  1) dx  
0

3

Nếu kết quả của (1) dẫn đến S = k > 0 thì điều giả định là
đúng
 Vậy S = k.
Nếu kết quả của (1) dẫn đến S = m < 0 thì điều giả định là
sai

094.673.6868

0

1

 x3 x 2

29
x  x  4 dx   
 4 x  
2
 3
0 6



2



Và

(1)

a

-

Nguyễn Văn Dũng – THPT Hai Bà Trưng.





2

3

S 4   x  5  ( x  1) dx  
1

1

3

 x3 x2

22
 x  x  6 dx    
 6 x  
2
3
 3
1



2



 29 22  73
 
(đvdt)
3  3

 6

Vậy S  2

Nhận xét sau lời giải:
- Mới đầu nhìn bài tốn có thể thấy hơi khó, nhưng sau khi
cụ thể giả thiết và vẽ đồ thị của các hàm số, ta thấy bài
toán thật đơn giản.
- Tương tự như bài 10, bài 11- 12, ta không nên sử dụng
các phương pháp: xét dấu, đưa giá trị tuyệt đối ra ngoài
và phương pháp giả định để giải bài này.
Bài 14: Tính diện tích của hình phẳng giới hạn bởi đồ thị
hàm số y2 + x – 5 = 0 và x + y – 3 = 0
Nhận xét trước khi giải.
- Giả thiết của bài toán này cho hàm số y2 + x – 5 = 0 (có
bậc hai đối với y và bậc một đối với x) nên ta sẽ coi x là
hàm và y là biến.
- Việc coi x là hàm và y là biến không hề ảnh hưởng đến
kết quả bài tốn diện tích hình phẳng.
- Ta sẽ giải bài toán này theo cả 4 phương pháp.
Lời giải 1: (phương pháp xét dấu)
Từ giả thiết: y2 + x – 5 = 0  x = 5 - y2 (P)
và x + y – 3 = 0  x = 3 – y (d)
Khi đó phương trình tung độ giao điểm của (P) và (d) là:



Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 45


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Lưu ý rằng:
2

 x  1, khi x  (;1]  [1;)
( P1 )
y  x2  1   2
( P2 )
 x  1, khi x  (1;1)
( d1 )
 x  5, khi x  0
Và
y | x | 5  
 x  5, khi x  0 (d 2 )

Với các lưu ý trên ta thấy rằng bài toán này thuộc bài toán 3,
nên ta sẽ sử dụng phương pháp đồ thị để giải.
Lời giải: (phương pháp đồ thị)

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

- Bước 4: Kiểm tra kết quả sau khi tính S
 Nếu kết quả của (1) dẫn đến S = k > 0 thì điều giả định là
đúng  Vậy S = k.
 Nếu kết quả của (1) dẫn đến S = m < 0 thì điều giả định
là sai, khi đó quay lại bước 3 và đổi dấu cộng (+) thành
trừ (-) và trừ (-)thành cộng (+)
 S = - m.
4. Một số chú ý khi giải bài tốn diện tích hình phẳng:
- Trong thực tế có rất nhiều bài tập để việc tính tốn bớt
phức tạp và trở nên đơn giản ta thường thay đổi vai trò của x và
y cho nhau, tức là x là hàm số và y là biến số, khi đó cơng thức
tính diện tích hình phẳng D của bài toán 1 và bài toán 2 là:
b

b

S   f ( y ) dy hoặc S   f ( y )  g ( y ) dy
a

a

- Phải điền kí hiệu “đvdt” (đơn vị diện tích) vào kết quả
cuối cùng trong các bài tốn diện tích hình phẳng.

- Phương trình hồnh độ giao điểm của đồ thị 2 hàm số
y  x 2  1 , y | x | 5 là: x 2  1 | x | 5  x = - 3 và x = 3.
Gọi S là diện tích hình phẳng cần tìm, từ đồ thị đã thì phần gạch
chéo chính là phần hình phẳng mà ta cần tính diện tích ( phần
hình phẳng này đối xứng nhau qua Oy).
Gọi S là diện tích cần tìm, ta có: S = S1 + S2 = 2S2 = 2(S3 + S4)

Trong đó S3 là phần hình phẳng được giới hạn bởi các
đường y  x  5 , y = - x2 + 1, x = 0, x = 1 và S4 là phần hình
phẳng được giới hạn bởi các đường y = x + 5, y = x2 - 1, x = 1,
x = 3.

Trang 44

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 13


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Phần thứ ba
BÀI TẬP MINH HỌA PHƯƠNG PHÁP
Trong phần này sẽ tập trung giới thiệu một số bài tập về
diện tích hình phẳng, với sự đa dạng về giả thiết của bài toán và
được giải bằng cả 4 phương pháp đã trình bày ở trên. Tuy nhiên
tùy thuộc vào từng bài toán cụ thể ta sẽ có những nhận xét về sự
lựa chọn phương pháp giải tối ưu nhất.
Bài 1:( Ví dụ 1 – SGK Giải tích 12- trang 115).

Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y = x3, trục hoành và hai đường thẳng x = - 1, x = 2.
Nhận xét trước khi giải.
- Giả thiết của bài 1 này có đủ giả thiết của bài tốn 1.
- Đây là bài toán đã được đề cập đến trong phần khảo sát
thực tế, ở đó bài tốn này được giải bằng phương pháp
xét dấu của biểu thức trong giá trị tuyệt đối.
- Bây giờ ta sẽ giải bài toán này bằng 3 phương pháp nữa,
đó là: phương pháp đưa dấu giá trị tuyệt ra ngoài,
phương pháp đồ thị và phương pháp giả định.
Lời giải 1: (phương pháp đưa dấu giá trị tuyệt đối ra ngồi)
Ta có x3 = 0  x = 0  [- 1; 2], khi đó hình phẳng có diện tích
là:
2

0

S   x dx   | x |dx   | x 3 |dx
0

x4 0
x4 2 1
17
  x dx   x dx 

 4
(đvdt)

1
0

4
4
4
4
1
0
2

3

2

S = S1 + S2    x 2  dx 
x
3 
2

3

Nhận xét sau lời giải 1:
- Sau khi tách tích phân ta nhận thấy rằng biểu thức f(x) =
x3 luôn xác định dấu trên các đoạn [- 1; 0] và [0; 2], nên
ta có thể đưa dấu giá trị tuyệt đối ra ngoài.

3

32


2

 8 x2 
  dx  4 ln 2 (đvdt)
x 4 

Nhận xét sau lời giải:
- Từ hình vẽ ta thấy rằng phần hình phẳng cần tính diện
tích (được giới hạn bởi 4 đường tự cắt) phải được chia
nhỏ thành 2 phần có diện tích tương ứng S1 và S2, trong
đó S1 là phần hình phẳng được giới hạn bởi các đường
y  x2 , y 

2
,x=
x

3

2 , x = 2 và S2 là phần hình phẳng

x2
8
được giới hạn bởi các đường y  , y  , x = 2, x =
4
x
3
32 .

3

1

0

2

2

3

1

Từ hình vẽ bên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Khi đó diện tích của hình phẳng cần tìm là:

Mới đầu nhìn bài tốn có thể thấy hơi khó, nhưng sau khi
cụ thể giả thiết và vẽ đồ thị của các hàm số, ta thấy bài
toán thật đơn giản.
- Tương tự như bài 10, bài 11, ta không nên sử dụng các
phương pháp: xét dấu, đưa giá trị tuyệt đối ra ngoài và
phương pháp giả định để giải bài này.
Bài 13: Tính diện tích của hình phẳng giới hạn bởi các
đường y  x 2  1 , y | x | 5
-

Nhận xét trước khi giải.

Trang 14

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 43


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

x2
, x = 0, x = 2 và S2 là phần hình phẳng
8
x2
8
được giới hạn bởi các đường y  , y  , x = 2, x = 4.
8
x
y  x2 , y 

-

-

Mới đầu nhìn bài tốn có thể thấy hơi khó, nhưng sau khi
cụ thể giả thiết và vẽ đồ thị của các hàm số, ta thấy bài
toán thật đơn giản.
Bài tập này không nên sử dụng các phương pháp: xét
dấu, đưa giá trị tuyệt đối ra ngoài và phương pháp giả
định.

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Lời giải sẽ sai nếu như ta khơng tách tích phân mà đưa
ngay dấu giá trị tuyệt đối ra ngoài sau khi lập S, tức là

-

2

2

viết S   x 3 dx   x 3dx , bởi biểu thức f(x) = x3 chưa xác
1

1

định dấu trên đoạn [- 1; 2].
Lời giải 2: (phương pháp đồ thị)
Ta có x3 = 0  x = 0  [- 1; 2], Từ hình vẽ ta có phần gạch
chéo chính là phần hình phẳng cần tính diện tích. Ta có
0

2

S = S1 + S2 =   x 3 dx   x 3 dx =
1

0

1
17
 4  (đvdt)
4
4

Bài 12: Tính diện tích của hình phẳng giới hạn bởi đồ thị
8
x2
2
hàm số y  x , y  , y  , y  .
x
4
x
2

Nhận xét trước khi giải.
- Bài tập này ở dạng bài toán 3 ta nên sử dụng phương
pháp đồ thị để giải.
Lời giải : (phương pháp đồ thị)
- PT hoành độ giao điểm của ĐTHS y  x 2 và y 
 x=

3

2
2
là:

 x2
x
x

2

- PT hoành độ giao điểm của ĐTHS y  x 2 và y 

8
8
là:
 x2
x
x

 x=2

- PT hoành độ giao điểm của ĐTHS y 

x2
2
và y  là:
4
x

2 x2

 x=2
x
4

- PT hoành độ giao điểm của ĐTHS y 
8 x2

 x=
x
4

Trang 42

3

x2
8
và y  là:
4
x

Nhận xét sau lời giải 2:
Phần hình phẳng cần tính có diện tích S được tách thành tổng
của 2 phần hình phẳng có diện tích lần lượt là S1 và S2. Trong
đó S1 là diện tích hình phẳng giới hạn bởi các đường y = x3, y =
0, x= -1, x = 0( phần nằm dưới trục hồnh) và S2 là diện tích
hình phẳng giới hạn bởi các đường y = x3, y = 0, x= 0, x = 2(
phần nằm trên trục hồnh).
Lời giải 3: (phương pháp giả định)
Ta có x3 = 0  x = 0  [- 1; 2], khi đó hình phẳng có diện tích
là:
2

0

2

1

1

0

2

1

0

1
17
 4
(???)
4
4

32

Bài tốn diện tích hình phẳng

0

S   x 3 dx   | x 3 |dx   | x 3 |dx   x 3dx   x 3dx

Bài tốn diện tích hình phẳng.

Trang 15


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Nhận xét sau lời giải trên:
- Sau khi tách thành 2 tích phân, ta đã tiến hành bỏ dấu giá
trị tuyệt đối với sự giả định rằng tích phân đầu tiên mang
0

dấu cộng (tức là

| x

0
3

1

|dx   x 3dx ) và tích phân thứ hai
1

2

2

mang dấu trừ (tức là:  | x 3 |dx    x 3dx ).
0

-

-

17
( do diện tích ln dương). Do vậy ta cần thêm dấu
4

trừ (-) vào sau tất cả các dấu bằng(=) bắt đầu từ khi bỏ
dấu giá trị tuyệt đối.
Bây giờ ta sẽ trình bày lại như sau:
2

0

094.673.6868

- Hoành độ giao điểm của 2 ĐTHS y  x 2 và y 

x2
là nghiệm
8

x2
của phương trình:
 x2  x = 0

8

- Hồnh độ giao điểm của 2 ĐTHS y  x 2 và y 

8
là nghiệm
x

của phương trình:

0

Nhưng điều giả định trên đây đã sai vì kết quả diện tích S
=

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

8
 x2  x = 2
x

- Hoành độ giao điểm của 2 ĐTHS y 
của phương trình :

x2
8
và y  là nghiệm
8
x

8
x2

 x =4
x
8

2
0 3


S   x dx   | x |dx   | x |dx    x dx   x 3 dx 
1
1
0
0
 1

4
4
 x 0 x 2
    1  4    17 (đvdt)
 


4
 4

 4 1 4 0
3

2

3

3

Bài 2:(Bài 26 – SGK Giải tích 12 Nâng cao – trang 167).
Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số
7
y = sinx + 1, trục hoành và hai đường thẳng x = 0, x =
.
6

Nhận xét trước khi giải.
-

Giả thiết của bài 2 này có đủ giả thiết của bài tốn 1.

-

Bây giờ ta sẽ giải bài toán này bằng cả 4 phương pháp
nữa, đó là: phương pháp xét dấu, phương pháp đưa dấu
giá trị tuyệt ra ngoài, phương pháp đồ thị và phương
pháp giả định.

Lời giải 1: (phương pháp xét dấu)

Trang 16

Bài tốn diện tích hình phẳng

Từ hình vẽ bên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Khi đó diện tích của hình phẳng cần tìm là:
S = S1 + S2
2

2

4

4

 2 x2 
 8 x2 
7 x3
x3 
  8 ln | x |    8 ln 2
   x  dx     dx 
8 
x 8 
24 0 
24  2
0
2

Nhận xét sau lời giải:
- Từ hình vẽ ta thấy rằng phần hình phẳng cần tính diện
tích (được giới hạn bởi 3 đường tự cắt) phải được chia
nhỏ thành 2 phần có diện tích tương ứng S1 và S2, trong

đó S1 là phần hình phẳng được giới hạn bởi các đường

Bài tốn diện tích hình phẳng.

Trang 41


Nguyễn Văn Dũng – THPT Hai Bà Trưng.
2





4



094.673.6868



  x  2 x  2   2 x  2 dx   x 2  2 x  2  6 x  14  dx
2

Nguyễn Văn Dũng – THPT Hai Bà Trưng.


Ta có sinx + 1 = 0  sinx = - 1  x = - + k2  (k  Z) 
2

2

0

16
(đvdt)
  x dx   x  8 x  16 dx 
3
0
2
2

4

2

2

Nhận xét sau lời giải:
- Qua bài tập trên ta thấy rằng, có những bài tập về tính
diện tích hình phẳng thường giả thiết của bài toán là
chưa cụ thể, nên trước khi lựa chọn phương pháp giải ta
phải cụ thể hóa giả thiết của bài tốn.
- Từ hình vẽ ta thấy rằng phần hình phẳng cần tính diện
tích (được giới hạn bởi 3 đường tự cắt) phải được chia
nhỏ thành 2 phần có diện tích tương ứng S1 và S2, trong
đó S1 là phần hình phẳng được giới hạn bởi các đường y
= x2 – 2x + 2, y = - 2x + 2, x = 0, x = 2 và S2 là phần
hình phẳng được giới hạn bởi các đường y = x2 – 2x + 2,

y = 6x -14, x = 2, x = 4.
- Mới đầu nhìn bài tốn có thể thấy hơi khó, nhưng sau khi
cụ thể giả thiết và vẽ đồ thị của các hàm số, ta thấy bài
toán thật đơn giản.
- Bài tập này không nên sử dụng các phương pháp: xét
dấu, đưa giá trị tuyệt đối ra ngoài và phương pháp giả
định.
Bài 11: Tính diện tích của hình phẳng giới hạn bởi đồ thị
8
x2
hàm số y  x , y  , y  .
x
8
2

094.673.6868

khơng có nghiệm thuộc đoạn [0;

7
].
6

Vậy diện tích của hình phẳng cần tìm là:
7
6

S   | sin x  1 | dx =
0

7
6

 (sin x  1)dx =
0

7
3

 1 (đvdt)
6
2

Nhận xét sau lời giải 1:
- Trong lời giải trên ta đã sử dụng một kết quả cơ bản của
tốn lượng giác, đó là: sinx  -1  sinx + 1  0 
|sinx +1| = sinx + 1
Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)
7
6

S   | sin x  1 | dx
0

7
6



7

 (sin x  1 |)dx  ( cos x  x) 06 
0

7
3

 1 (đvdt)
6
2

Nhận xét sau lời giải 2:
- Do biểu thức f(x) = sinx + 1 xác định dấu trên đoạn [0;

7
],
6

nên ta có thể đưa dấu giá trị tuyệt đối ra bên ngồi dấu tích
phân.
Lời giải 3: (phương pháp đồ thị)

Nhận xét trước khi giải.
- Bài tập này ở dạng bài toán 3 ta nên sử dụng phương
pháp đồ thị để giải.
Lời giải : (phương pháp đồ thị)

Trang 40

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 17


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Từ hình vẽ trên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Ta có
7
6

S

 (sin x  1)dx



0

7
3

 1 (đvdt)
6
2

Nhận xét sau lời giải 3:
-

Vẽ đồ thị hàm số lượng giác là một việc tương đối khó,
xong cũng khơng phức tạp lắm trong bài tốn này.

-

Đồ thị hàm số y = sinx + 1 được suy từ đồ thị hàm số y=
sinx bằng cách tịnh tiến đồ hàm số này song song với trục
Oy theo vectơ tịnh tiến OM =(0; 1).

-

Với học sinh trung bình khá trở xuống có thể khơng thực
hiện được theo phương pháp này.

-

Do phần hình phẳng nằm trên trục hồnh nên
7
6

7
6

S   | sin x  1 | dx   (sin x  1)dx
0

0

Lời giải 4: (phương pháp giả định)
7
6

7
6

S   | sin x  1 | dx   (sin x  1)dx 
0

0

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Bài 10: Tính diện tích của hình phẳng giới hạn bởi parabol
(P) y = x2 – 2x + 2 và các tiếp tuyến của (P) đi qua điểm
A(2; -2).
Nhận xét trước khi giải.
- Giả thiết của bài toán này chưa cụ thể, do vậy việc đầu
tiên ta cần cụ thể hóa giả thiết, tức là phải viết phương
trình tiếp tuyến của (P) qua A(2; -2).
- Sau khi cụ thể hóa giả thiết ta sẽ thấy rằng bài này thuộc
vào bài toán 3.
- Với bài tập ở dạng bài toán 3 ta nên sử dụng phương
pháp đồ thị để giải.
Lời giải: (phương pháp đồ thị)
Phương trình các tiếp tuyến của (P) qua điểm A(2; - 2) là d1: y =

- 2x + 2 và d2 : y = 6x – 14.
- Hoành độ giao điểm của d1 và d2 là nghiệm của phương trình:
- 2x + 2 = 6x – 14  x = 2
- Hoành độ giao điểm của (P) và d1 là nghiệm của phương trình
- 2x + 2 = x2 – 2x + 2  x = 0
- Hoành độ giao điểm của (P) và d2 là nghiện của phương trình
x2 – 2x + 2 = 6x – 14  x = 4

7
3

 1 (đvdt).
6
2

Nhận xét sau lời giải 4:
- Do phương trình sinx + 1 = 0 khơng có nghiệm thuộc đoạn [0;
7
], nên ta khơng cần phải tách tích phân mà tiến hành bỏ dấu
6

giá trị tuyệt đối luôn với sự giả định là dấu cộng (+) trước dấu
tích phân.
7
3
- Kết quả sau khi tính S 

 1 > 0 nên việc giả định về
6

2

Từ hình vẽ bên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Khi đó diện tích của hình phẳng cần tìm là:
S = S1 + S2

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

dấu ở trên là đúng.

Trang 18

Trang 39


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Từ hình vẽ bên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Khi đó diện tích của hình phẳng cần tìm là:
S = S1 + S2 + S3
1



3







  x  3  ( x 2  4 x  3) dx   x  3  ( x 2  4 x  3) dx
1

0

5





  x  3  ( x 2  4 x  3) dx
3

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Bài 3:( Câu I.3 – Đề thi TN THPT năm 2006 – Phân ban).
Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số y =
- x3 + 3x2 và trục hoành.
Nhận xét trước khi giải.
- Bài 3 này thuộc vào dạng của bài tốn 1 nhưng cịn thiếu
giả thiết là cận lấy tích phân.

- Ta sẽ giải bài tốn này bằng cả 4 phương pháp nữa, đó
là: phương pháp xét dấu, phương pháp đưa dấu giá trị
tuyệt ra ngoài, phương pháp đồ thị và phương pháp giả
định.
Lời giải 1: (phương pháp xét dấu)
Ta có phương trình: - x3 + 3x2 = 0 có 2 nghiệm là x = 0 và x =
3.
Và có bảng xét dấu của f(x) = - x3 + 3x2 như sau.
x
0
3
f(x)
+
+
Vậy hình phẳng đã cho có diện tích là:
3

3

3

 x3 5x 2  1  x3 3x 2
 3  x 3 5 x 2  5 109
  
 
   
 6 x     
( đvdt)
2  0  3
2

2  3
6
 3
1  3

 x4

27
S   |  x  3 x | dx   ( x  3x )dx   
 x 3  
(đvdt)
 4
0 4
0
0

Nhận xét sau lời giải 2:
- Trên đây ta đã sử dụng phương pháp đồ thị để giải bài
tập 9, nhận thấy rằng phương pháp rất hay, lời giải sáng
sủa mà không phải sử dụng cách đánh giá như trong
phần khảo sát thực tế.
- Trong cách giải này ta đã tách diện tích S thành tổng của
3 phần có diện tích tương ứng là S1, S2, S3 bởi các đường
thẳng x =1 và x= 3; với S1 là diện tích hình phẳng giới
hạn bởi các đường y = x2 - 4x + 3 , y = x + 3, x=0, x
=1; S2 là diện tích hình phẳng giới hạn bởi các đường
y=- x2+4x- 3 y = x + 3, x=1, x= 3 và S3 là diện tích của
hình phẳng giới hạn bởi các đường y = x2 - 4x + 3 , y =
x + 3, x= 3, x = 5.

Nhận xét sau lời giải 1:
- Việc xét dấu biểu thức f(x) = - x3 + 3x2 là khơng khó khăn
gì bởi f(x) là một đa thức bậc 3 đối với x.
- Ta cũng có thể nhận xét f(x) = - x3 + 3x2 = x2(3 – x)  0 ,
 x  [0; 3]

Trang 38

Bài toán diện tích hình phẳng.

Bài tốn diện tích hình phẳng

3

2

3

2

Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngồi)
Phương trình: - x3 + 3x2 = 0 có 2 nghiệm là x = 0 và x = 3.
3
2
 biểu thức f(x) = - x + 3x xác định dấu trên đoạn [0; 3], nên

diện tích của hình phẳng cần tìm là.
3

3

3

 x4

27
S   |  x  3 x | dx   ( x  3 x )dx   
 x 3  
(đvdt)
4
 4
0
0
0
3

2

3

2

Trang 19


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Nhận xét sau lời giải 2:

- Do biểu thức f(x) = - x3 + 3x2 luôn xác định dấu trên đoạn [0;
3], nên ta có thể đưa dấu giá trị tuyệt đối ra bên ngồi dấu tích
phân.
Lời giải 3: (phương pháp đồ thị)

Nguyễn Văn Dũng – THPT Hai Bà Trưng.
-

Trong lời giải trên, sau khi xác định cận tích phân và lập
cơng thức tính S, ta đã tiến hành bỏ dấu giá trị tuyệt đối
với sự giả định rằng dấu cộng (+) trước dấu tích phân.

-

Nhưng điều giả sử này là sai vì kết quả của S = 

-

diện tích ln dương). Do vậy ta cần thêm dấu trừ (-) vào
sau tất cả các dấu bằng(=) bắt đầu từ khi bỏ dấu giá trị
tuyệt đối.
Bây giờ ta sẽ trình bày lại như sau:
1

1
3

S   x  x dx   
0

Từ hình vẽ trên ta có phần gạch chéo chính là phần hình phẳng
cần tính diện tích. Ta có
3

3
3

 x4

27
    x 3  
 4
0 4

2

S   ( x  3x )dx
0

(đvdt)

Nhận xét sau lời giải 3:
- Đây là một câu hỏi phụ kèm theo một bài toán khảo sát
hàm số nên thường các em đều sử dụng phương pháp đồ
thị để giải, bởi rất dễ dàng các em có thể xác định được
phần hình phẳng cần tính diện tích.
- Do phần hình phẳng nằm trên trục hồnh nên ta sẽ có.
3

3

S   |  x 3  3 x 2 | dx   ( x 3  3x 2 )dx
0

0

Lời giải 4: (phương pháp giả định)
Ta có phương trình: - x3 + 3x2 = 0 có 2 nghiệm là x = 0 và x =
3.
Khi đó hình phẳng cần tìm có diện tích là
3

3

3

 x4

27
(đvdt)
S   |  x  3 x | dx   ( x  3x )dx     x 3  
 4
0 4
0
0
3

2

3

2

Nhận xét sau lời giải 4:

Trang 20

Bài tốn diện tích hình phẳng

094.673.6868



1
( do
12



x  3 x dx

0
1

2 3 33 4 
2 3 1
 
x 
x      
4

3
0
 3 4  12
Nhận xét sau khi giải.
- Sau khi sử dụng cả 4 phương pháp trên ta thấy rằng, ta nên sử
dụng 2 phương pháp: đưa dấu giá trị tuyệt đối ra ngoài và
phương pháp giả định để giải bài tập này.
Bài 9:( Câu III.2 – Đại học khối A năm2002).
Tính diện tích của hình phẳng giới hạn bởi các đường
y = |x2 – 4x + 3| và y = x + 3.
Nhận xét trước khi giải.
- Giả thiết của bài toán này thuộc dạng của vào bài toán 3
bởi với hàm số y = |x2 – 4x + 3| sẽ tương đương với 2
hàm số là: y = x2 – 4x + 3 ( khi x  (-  ; 1)  (3; +  )
và y = - x2 + 4x - 3 (khi x  (1; 3).
- Đây là bài tập mà ta đã đề cập đến trong phần khảo sát
thực tế và đã sử dụng phương pháp xét dấu để tìm diện
tích. Bây giờ ta sẽ sử dụng thêm phương pháp đồ thị để
giải bài toán này.
Lời giải 2: (phương pháp đồ thị)
Ta xét phương trình hồnh độ giao điểm của 2 ĐTHS đã cho là:
|x2 – 4x + 3| = x + 3  x = 0 hoặc x = 5 (xem hình vẽ)

Bài tốn diện tích hình phẳng.

Trang 37


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

không cần phải xét dấu của biểu thức f(x) – g(x) = x 3
x mà vân tính được tích phân.
- Do 2 ĐTHS đã cho chỉ có 2 giao điểm (tương ứng với 2
cận lấy tích phân) nên ta khơng phải tách tích phân mà
đưa dấu giá trị tuyệt đối ra ngoài ngay sau khi lập S.
Lời giải 3: (phương pháp đồ thị)

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

- Do PT: - x3 + 3x2 = 0 chỉ có 2 nghiệm là x = 0 và x = 3, nên
ta không cần phải tách tích phân mà bỏ dấu giá trị tuyệt đối
luôn với sự giả định là dấu cộng (+) trước dấu tích phân.
- Kết quả sau khi tính S 

1

S

1

x  x dx   (3 x  x )dx 
3

0

0

3 2 1

 
(đvdt)
4 3 12

Nhận xét sau lời giải 3:
- Việc vẽ đồ thị của hai hàm số y  x , y  3 x là một khó
khăn với các em học sinh, nên đây cũng là một phương
pháp khó.
- Tuy nhiên khi đã vẽ được đồ thị rồi thì việc tính tốn trở
nên đơn giản.
Lời giải 4: (phương pháp giả định)
1

1

S 

x  3 x dx  

0

0



1

2 3
1
2 3 33 4 

x  3 x dx  
x 
x    
4
12
3
0 3 4



(???)
Nhận xét sau lời giải 4:

27
> 0 nên việc giả định về dấu ở trên
4

là đúng.
Bài 4:( Câu II.2 – Đề thi TN THPT năm 2003).
Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số
y

Từ hình vẽ ta có phần gạch chéo chính là phần hình phẳng cần
tính diện tích. Ta có

094.673.6868

2 x 2  10 x  12
và đường thẳng y = 0.
x2

Nhận xét trước khi giải.
- Bài 4 này thuộc vào dạng của bài toán 1 nhưng cịn thiếu
giả thiết là cận lấy tích phân.
- Ta sẽ giải bài toán này bằng cả 4 phương pháp nữa, đó
là: phương pháp xét dấu, phương pháp đưa dấu giá trị
tuyệt ra ngoài, phương pháp đồ thị và phương pháp giả
định.
Lời giải 1: (phương pháp xét dấu)
Xét phương trình

2 x 2  10 x  12
 0  2 x 2  10 x  12  0
x2

 Phương trình có 2 nghiệm là x = -1 và x = 6.
2 x 2  10 x  12
Và có bảng xét dấu của f(x) 
như sau.
x2

x
-2
-1
f(x)
+
Vậy hình phẳng đã cho có diện tích là:

6
-

+

6
2 x 2  10 x  12
2 x 2  10 x  12
S 
dx   
dx  63  16 ln 8
x2
x2
1
1
6

Nhận xét sau lời giải 1:
-

Việc xét dấu biểu thức f(x) 

2 x 2  10 x  12
là khơng khó
x2

khăn vì các em học sinh đã được học từ lớp 10. Tuy nhiên

Trang 36

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 21


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

đây không phải là nhị thức bậc nhất hay tam thức bậc hai
nên cũng khơng ít em cịn lúng túng.
Để khắc phục khó khăn này ta có thể sử dụng thêm định lí
về dấu của đa thức.

-

Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)
6

2 x 2  10 x  12
S
dx 
x2
1



6

6

2 x 2  10 x  12
16 

1 x  2 dx  1  2 x  14  x  2 dx



 x 2  14 x  16 ln | x  2 |

6
1

 16 ln 8  63 = 63 – 16ln8 (đvdt)

Nhận xét sau lời giải 2:
- Do biểu thức f(x) 

2 x 2  10 x  12
luôn xác định dấu trên đoạn
x2

[-1; 6], nên ta có thể đưa dấu giá trị tuyệt đối ra bên ngồi dấu
tích phân.
Lời giải 3: (phương pháp đồ thị)
Từ hình vẽ bên ta có phần gạch chéo chính là phần hình
phẳng cần tính diện tích. Ta có
6

S

2

6

2

2 x  10 x  12
2 x  10 x  12
dx   
dx = 63 – 16ln8 (đvdt)
x2
x2
1
1



Nguyễn Văn Dũng – THPT Hai Bà Trưng.

Bài 8:( Bài 27b – SGK Giải tích 12 nâng cao-trang 167).
Tính diện tích của hình phẳng giới hạn bởi đồ thị hai
đồ thị hàm số y  x , y  3 x
Nhận xét trước khi giải.
- Bài toán này thuộc dạng của bài tốn 2 nhưng cịn thiếu giả
thiết là các cận lấy tích phân.
- Để giải bài tập này trước hết ta cần tìm cận lấy tích phân, nó
chính là hồnh độ giao điểm của đồ thị 2 hàm số y  x ,
y3 x.
Lời giải 1: (phương pháp xét dấu)

Đặt f(x)  x , g(x)  3 x ,
ta có: f(x) – g(x) = x - 3 x = 3 x (6 x  1) = 0
 x = 0 hoặc x = 1
mặt khác f(x) – g(x)  0  x  [0; 1]
Vậy diện tích hình phẳng cần tìm là
1

1
3

S   x  x dx   (3 x  x )dx 
0

0

1
(đvdt)
12

Nhận xét sau lời giải 1:
- Phương pháp này thực hiện tương đối khó đối với các em
học sinh vì ta khơng thể sử dụng bảng để xét được mà
phải cần xét bất phương trình f(x) – g(x)  0
- Nói chung nếu là các em học sinh trung bình khá trở
xuống không nên lựa chọn phương pháp này
Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)
1

S   x  3 x dx 
0

1





x  3 x dx 

0

2 3 1
 
(đvdt)
3 4 12

Nhận xét sau lời giải 2:
- Ở bài tập này ta thấy được sự tiện lợi của phương pháp
đưa dấu giá trị tuyệt đối ra ngồi dấu tích phân, đó là

Nhận xét sau lời giải 3:

Trang 22

094.673.6868

Bài tốn diện tích hình phẳng

Bài tốn diện tích hình phẳng.

Trang 35


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Trong bài này ta khơng phải tách tích phân, mà sau khi
lập cơng thức tính S ta tiên hành đưa dấu giá trị tuyệt đối
ra ngồi ln.
Lời giải 3: (phương pháp đồ thị)
-

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

2 x 2  10 x  12
đã được học trong chương
x2

-

Do hàm số y 

-

trình Tốn 12(chương trình nâng cao)nên khơng mấy khó
khăn để các em có thể khảo sát được hàm số này, và xác
định được phần hình phẳng cần tính diện tích.

Do phần hình phẳng nằm dưới trục hồnh nên ta sẽ có.
6

6

2 x 2  10 x  12
2 x 2  10 x  12
S
dx   
dx
x2
x2
1
1

Với chương trình Tốn 12 hiện tại các em học chương
trình cơ bản sẽ không khảo sát hàm phân thức bậc 2 trên
bậc 1, nên phương pháp này chỉ dùng cho các em học
theo chương trình nâng cao.

-

Từ hình vẽ ta có phần gạch chéo chính là phần hình phẳng cần
tính diện tích. Ta có
1

1



1



1

S   xe x  ex dx   ex  xe x dx   exdx   xe x dx =
0

0

0

0

e
- 1 (đvdt)
2

Nhận xét sau lời giải 3:
- Phải nói là khơng có học sinh và cả giáo viên làm theo cách
này, bởi vì rất khó để có thể vẽ ĐTHS y = (1 + ex)x.
- Phải có sự trợ giúp của các phần mềm vẽ đồ thị ta mới vẽ
được độ thị như trên.
Lời giải 4: (phương pháp giả định)
1

1



x



1

1
x

S   xe x  ex dx   ex  xe dx   exdx   xe dx 
0

0

0

0

e
1
2

Nhận xét sau lời giải 4:
- Do PT: f(x) = g(x) chỉ có 2 nghiệm là x = 0 và x = 1, nên ta
khơng cần phải tách tích phân mà tiến hành bỏ dấu giá trị tuyệt
đối luôn với sự giả định là dấu cộng (+) trước dấu tích phân.
- Kết quả sau khi tính S 

e

 1 > 0 nên việc giả định về dấu ở
2

trên là đúng.

Trang 34

Bài tốn diện tích hình phẳng

Lời giải 4: (phương pháp giả định)
Diện tích hình phẳng cần tìm là
6

6

S

2 x 2  10 x  12
2 x 2  10 x  12
dx


 x  2 dx
x2
1
1

6

6

16 

2
   2 x  14 
dx  x  14 x  16 ln | x  2 | 1  16 ln 8  63
x  2
1 

(???)
Nhận xét sau lời giải trên:
- Sau khi lập cơng thức tính S, ta khơng phải tách tích phân
mà tiến hành bỏ dấu giá trị tuyệt đối luôn với sự giả định
là dấu cộng (+) trước dấu tích (tức là
6

6

2 x 2  10 x  12
2 x 2  10 x  12
S
dx  
dx )
x2
x2
1
1

-

-

Nhưng điều giả định trên đây đã sai vì kết quả diện tích:
S = 16ln8 – 63 < 0 (do diện tích luôn dương). Do vậy ta
cần thêm dấu trừ (-) vào sau tất cả các dấu bằng(=) bắt
đầu từ khi bỏ dấu giá trị tuyệt đối.
Bây giờ ta sẽ trình bày lại như sau:

Bài tốn diện tích hình phẳng.

Trang 23


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

6

6

2 x 2  10 x  12
16 

S
dx     2 x  14 
dx
x2
x  2
1
1 



  x 2  14 x  16 ln | x  2 |



6
1

 (16 ln 8  63)  63  16 ln 8 (đvdt)

Bài 5: (ví dụ 2 – SGK giải tích 12 – trang 116)
Tính diện tích của hình phẳng giới hạn bởi các đường
y = sinx, y = c osx, x= 0 , x = 
Nhận xét trước khi giải.
- Bài 5 có đủ giả thiết của bài tốn 2, nên ta có thể áp dụng
ngay cơng thức tính S.
- Căn cứ vào giả thiết của bài tập và hãy lựa chọn phương
pháp giải phù hợp nhất.
- Ta sẽ giải bài toán này bằng cả 4 phương pháp nữa, đó
là: phương pháp xét dấu, phương pháp đưa dấu giá trị
tuyệt ra ngoài, phương pháp đồ thị và phương pháp giả
định.
Lời giải 1: (phương pháp xét dấu)
Đặt f(x) = sinx, g(x) = cosx,
ta có: f(x) – g(x) = 0  sinx – cosx = 0  tanx = 1


 x   k (k  Z), xét trên đoạn [0;  ]  x =

4

Ta thấy rằng: trên đoạn [0;

4


] ta thấy sinx > 0, cosx > 0
2

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

Lời giải 1: (phương pháp xét dấu)
Đặt f(x) = (e + 1)x, g(x) = (1 + ex)x. Phương trình hồnh độ
giao điểm của hai đường đã cho là (e + 1)x = (1 + ex)x  (ex –
e)x = 0  x = 0 hoặc x = 1.
Khi đó trên đoạn [0; 1] ta có: f(x) – g(x) = xex – ex = x(ex – e) <
0
Do đó diện tích hình phẳng cần tìm là.
1

1

S   f ( x )  g ( x) dx   xe x  ex dx
0
1

0



1



1

  ex  xe x dx   exdx   xe x dx 
0

0

0

e
- 1 (đvdt)
2

Nhận xét sau lời giải 1:
- Lời giải trên đây cũng là đáp án trong hướng dẫn chấm
của Bộ giáo dục.
- Tuy nhiên lời giải bằng phương pháp này không dễ làm
với cả đối tượng học sinh khá, giỏi do ta không thể xét
dấu trực tiếp biểu thức f(x) – g(x) = x(ex – e) bằng bảng
được mà ta phải xét dấu của nó một cách gián tiếp qua
việc giải bất phương trình f(x) > g(x)
Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)
1

1

S   f ( x)  g ( x ) dx   xe x  ex dx
0

0

1

1

1

 ex  xe dx   exdx   xe dx


nên ta có: f(x) – g(x) > 0  sinx > cosx  tanx > 0  x >
4

trên đoạn [ ;  ] thì sinx > 0, cosx < 0
2

nên f(x) – g(x) > 0  x  [ ;  ]
2

Vậy tóm lại: f(x) – g(x) > 0 khi x  [ ;  ]
4

Nhận xét sau lời giải 2:

- Phương pháp đưa dấu giá trị tuyệt đối ra ngồi dấu tích
phân vẫn tỏ ra rất hiệu quả với các bài tốn mà ta khơng
thể xét được dấu của biểu thức.

Trang 24

Bài tốn diện tích hình phẳng.

Bài tốn diện tích hình phẳng



x

0

Vậy S 

x

0

0

e
e
 1 = - 1 (đvdt)
2
2

Trang 33


Nguyễn Văn Dũng – THPT Hai Bà Trưng.

094.673.6868

- Do phần hình phẳng cần tính diện tích có trục đối xứng là Oy
nên ta có thể viết S 

2 2



2

4

2 2

2

x
x

dx  2
4 4 2

2 2

2

4


0

2

x
x

dx
4 4 2

Nguyễn Văn Dũng – THPT Hai Bà Trưng.

]
4
Vậy diện tích của hình phẳng đã cho là

và f(x) – g(x) < 0 khi x  [0;


Lời giải 4: (phương pháp giả định)
2 2

S

4


2 2
2 2

2


0

x2
x2

dx  2
4 4 2

2 2



4

0





2

16  x dx 

0

1
2 2

0


4



  | sin x  cos x | dx   | sin x  cos x | dx

4

0


4

2 2
2

 x dx  I

1

 I2


4

0

8
3

8
4
= 2  + (đvdt)
3
3

Nhận xét sau lời giải 4:
- Do PT f(x) = g(x) chỉ có 2 nghiệm x = - 2 2 và x = 2 2 , nên
ta khơng cần phải tách tích phân mà tiến hành bỏ dấu giá trị
tuyệt đối với sự giả định là dấu cộng (+) trước dấu tích phân.
- Kết quả sau khi tính S = 2  +



   sin x  cos x dx   sin x  cos x dx = 2 2 (đvdt)

0

tương tự lời giải 1, ta có I1 = 2  + 4 và I2 
Vậy S = 2  + 4 -

S   | sin x  cos x | dx

x2
x2

dx
4 4 2

2
2 

 4  x  x dx

4 4 2 


2 2

094.673.6868

4
> 0 nên việc giả định về dấu
3

Nhận xét sau lời giải 1:
- Do việc xét dấu của biểu thức f(x) – g(x) = sinx – cosx là
không đơn giản bởi ta không thể dùng bảng như các ví dụ trên
nữa, nên có rất ít các em học sinh có thể làm được theo phương
pháp này.

- Để xét được dấu của biểu thức trên ta phải chuyển qua các
việc xét bất phương trình f(x) – g(x) > 0.
Lời giải 2: (phương pháp đưa dấu giá trị tuyệt đối ra ngoài)

4



ở trên là đúng.
Bài 7:( Câu IV.1 – Đại học Khối A năm 2007).
Tính diện tích của hình phẳng giới hạn bởi các đường
y = (e + 1)x, y = (1 + ex)x
Nhận xét trước khi giải.
- Bài toán này thuộc dạng của bài toán 2 nhưng cịn thiếu
giả thiết là các cận lấy tích phân.
- Để giải bài tập này trước hết ta cần tìm cận lấy tích phân,
nó chính là hồnh độ giao điểm của đồ thị 2 hàm số y =
(e + 1)x, y = (1 + ex)x .

Nhận xét sau lời giải 2:

Trang 32

Bài tốn diện tích hình phẳng.

Bài tốn diện tích hình phẳng



S   | sin x  cos x | dx   | sin x  cos x | dx   | sin x  cos x | dx


4




4

0

0



 sin x  cos x dx   sin x  cos x dx

4

0





  cos x  sin x  04   cos x  sin x  

4

 S = 2 2 (đvdt)

Trang 25